基于模糊算法的水下機器人路徑規劃研究

王妹婷，陸柳延，齊永鋒，呂學智，蔣偉，李生權

(揚州大學能源與動力工程學院，江蘇揚州225127)

水下機器人是一種工作于水下的極限作業機器人，由于水下工作環境具有復雜性和不確定性，提高自主式水下機器人智能化的關鍵環節——路徑規劃研究顯得尤為重要。常用的局部路徑規劃算法有勢場法、A*算法、柵格法及模糊算法［1－3］。考慮到水下環境的復雜性，測距聲吶所得的環境信息都是近似、不完善的，并伴有一定的噪聲干擾［4］，而模糊控制器的最大優點就是能夠采用輸入的模糊信息［5］進行控制。此外，水下機器人的動力學模型極其復雜，是一個典型的非線性系統［6］。針對這類特殊控制對象，提出了一種結合視線導航原理［7］和模糊算法的未知環境下水下機器人實時路徑規劃策略，應用該策略，可于障礙物環境中，自動尋找一條從起始點到目標點的無碰撞路徑。

依據障礙物的不同形狀大小，采用不同方式求取機器人與障礙物之間距離以及目標點、機器人與障礙物三者之間的夾角［8］。此外，在MATLAB 仿真中，根據障礙物特征，對模糊控制規則表進行修改:障礙物較小時，以路徑最短最平滑為主;障礙物較大時，以嚴格快速避開障礙物為主。

1 工作原理

假設水下機器人勻速運動，首先，通過短基線系統，實時得到機器人與目標預定點的相對位置信息;利用測距聲吶對其運動前方的±90°范圍內進行實時探測，得到環境信息［9］。實時計算機器人與障礙物最近點的距離d，以及障礙物最近點、水下機器人、目標點三者間的夾角α，如圖1所示。通過模糊控制器進行實時模糊推理，得到避障狀態下水下機器人所需轉動的偏轉角，從而使得水下機器人有效地避開障礙物，安全到達設定目標點。

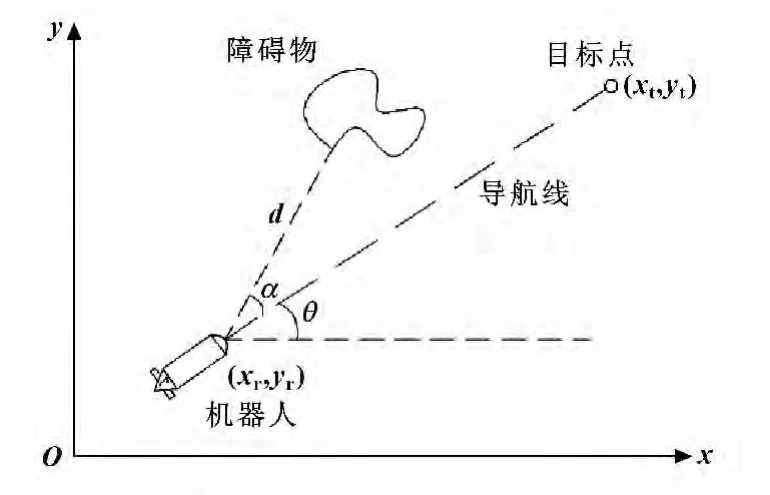
圖1 視線導航原理圖

1.1 距離d 的求取

與工作環境尺寸相比，障礙物尺寸較小的情況下，障礙物大小、形狀均可忽略不計，視為一個點，距離d 為機器人與該障礙物兩點之間的距離，公式為:

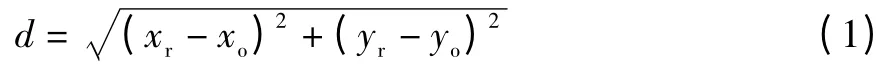
其中，(xr，yr)為機器人當前坐標，(xo，yo)為障礙物坐標。

反之，當障礙物尺寸較大且形狀不規則時，根據障礙物的邊緣坐標信息，近似變換為矩形障礙物，如圖2所示，得到矩形的4 個坐標點，以方便求取水下機器人與障礙物的最小距離點。

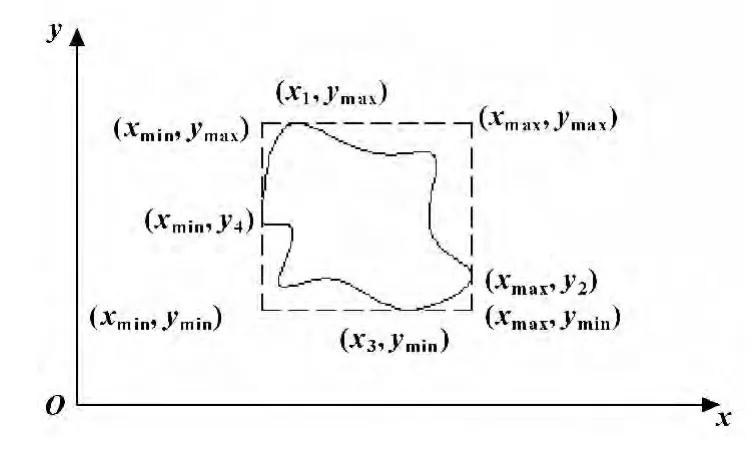
圖2 不規則圖形矩形化

矩形障礙物上距離水下機器人最近點與兩者相對位置有關，為求取水下機器人與矩形障礙物最近點的距離，針對機器人位于矩形障礙物的8 個區域分別討論，如圖3所示。

矩形障礙物與水下機器人之間的最近距離點可表示為:水下機器人位于1 區域，即xr≤xmin，yr≤ymin時，最近距離點d_node 坐標為(xmin，ymin);水下機器人位于2 區域，即xmin＜xr≤xmax，yr≤ymin時，d_node坐標為(xr，ymin);水下機器人位于3 區域，即xr＞xmax，yr≤ymin時，d_node 坐標為(xmax，ymin);水下機器人位于4 區域時，即xr≥xmax，ymin＜yr≤ymax時，d_node 坐標為(xmax，yr);水下機器人位于5 區域，即xr≥xmax，yr＞ymax時，d_node 坐標為(xmax，ymax);水下機器人位于6 區域，即xmin≤xr＜xmax，yr≥ymax時，d_node 坐標為(xr，ymax);水下機器人位于7 區域，即xr＜xmin，yr≥ymax時，d_node 坐標為(xmin，ymax);水下機器人位于8 區域，即xr≤xmin，ymin＜yr＜ymax時，d_node 坐標為(xmin，yr)。

水下機器人與矩形障礙物間的距離轉化為水下機器人與實時得到的矩形障礙物上最近距離點兩點之間的距離:

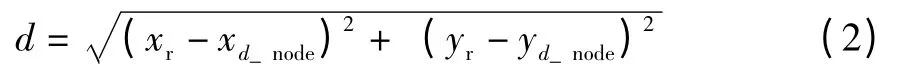
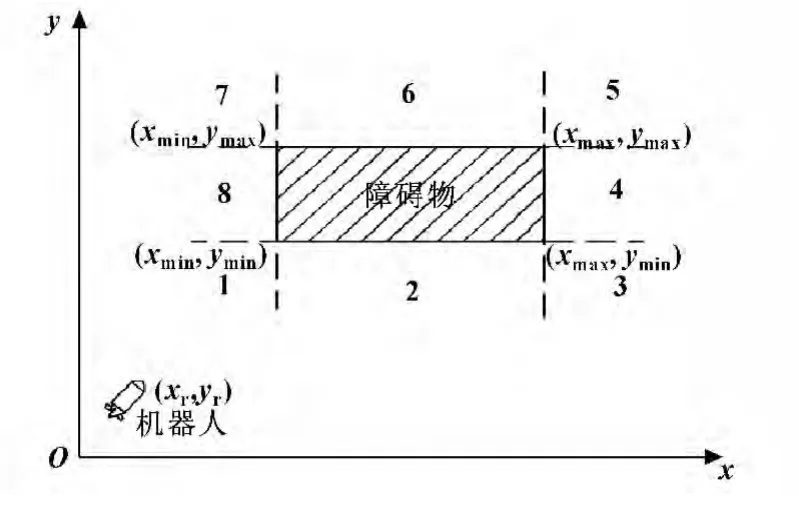
圖3 水下機器人與矩形障礙物的相對位置示意圖

1.2 夾角α 的求取

通過機器人當前位置、障礙物位置、目標位置三點坐標，能夠得到夾角α。因機器人的避障環境為其運動前方的±90°范圍內，將連接機器人與目標點的導航線作為分界線，當障礙物在導航線左側時設α為正;反之，α 為負。故

式中:a 為機器人與實時障礙物最近點的距離;b 為機器人與目標點的距離;c 為實時障礙物最近點與目標點的距離。

2 模糊控制器研究

基于模糊算法的水下機器人避障控制系統如圖4所示，其中模糊控制器由模糊量化、模糊規則、模糊推理和反模糊化接口4 部分組成［10］。由短基線系統得到目標的位置信息，由多個測距聲吶實時測得的與障礙物的距離信息，經過信息融合計算后所得到的距離d，以及障礙物與機器人、目標的夾角α，同時作為模糊控制器的輸入。輸入量經過模糊控制器進行模糊推理，最終得到水下機器人的偏轉角φ，然后水下機器人以新的方向進行運動。

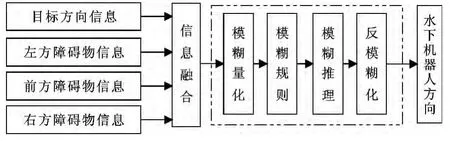
圖4 水下機器人避障控制系統示意圖

此處采用最簡單的信息融合技術，即每個方向的距離信息中，取其中較小的一個數據作為該方向的輸入，然后在每個方向上提取的距離信息中取最小的作為這一時刻的距離信息。

2.1 模糊集、模糊論域及隸屬函數確立

模糊控制輸入為水下機器人與障礙物的最小距離d、兩視線導航角的夾角α，輸出為水下機器人在t時刻所需的偏轉角φ。

由于測距聲吶的測量距離達30 m，系統設定的障礙物影響距離d 為10 m，即d 的論域為［0，100］，用模糊語言定義的模糊集為 D ={VS，S，M，B，VB }。其中，VS 表明距離極小，VB 表明距離極大。

為了判斷障礙物相對于目標的位置，設定障礙物、機器人、目標三者夾角α 的論域為［－ 90°，90°］，用模糊語言定義的模糊集為α = {NL，NS，Z，PS，PL}。其中，Z 表明障礙物在導航線上，N表示負，即設定的障礙物在導航線右側，反之，P 表示障礙物在導航線左側;L 表示角度大，S 則表示角度小。輸出偏轉角φ 設定為向左轉為負，向右轉為正，偏轉角φ 的論域為［－45°，45°］，同樣用模糊語言定義的模糊集為α= {NL，NS，Z，PS，PL}。

根據輸入輸出的模糊論域設定合適的模糊語言變量，在此均采用三角形隸屬度函數來反應模糊集合的模糊性。

2.2 模糊控制規則庫的建立與模糊推理

水下機器人在恒速運動過程中的避障原則為:在障礙物的影響距離范圍內，當障礙物在航線左側時，機器人向右側繞行，當障礙物在航線上或者右側時，機器人向左側繞行;除此之外，機器人沿著導航線，向目標方向前進。

依據障礙物的不同尺寸大小，提出以下兩種控制器設計要求:當障礙物大小在整個工作環境下可忽略不計時，以路徑能夠實現平滑最短為主，防止水下機器人頻繁過大的角度偏轉導致的振蕩;當障礙物較大的情況下，由于水下機器人運動速度比較快，所以在測出障礙物的同時就應開始偏轉，以免機器人無法安全繞行。因此，設定兩套控制規則，分別如表1、表2所示，并在仿真過程中，根據障礙物的大小，調節控制器中輸出偏轉角的大小及障礙物影響距離，可更好地完成機器人避障要求。

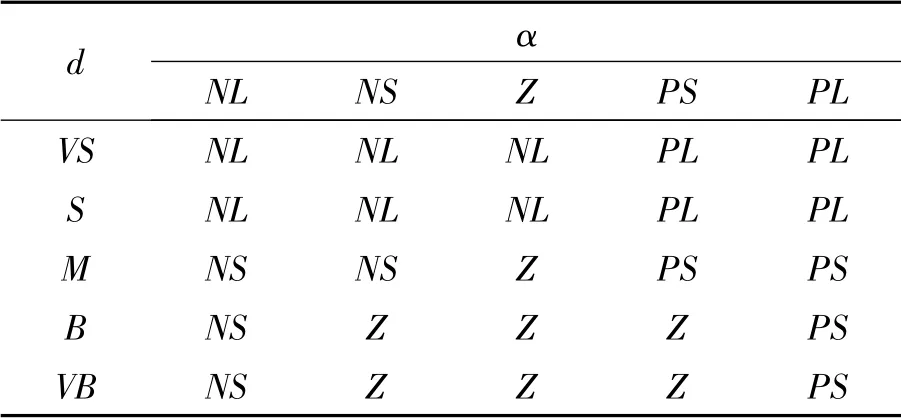
表1 障礙物較小時偏轉角φ 的模糊規則表

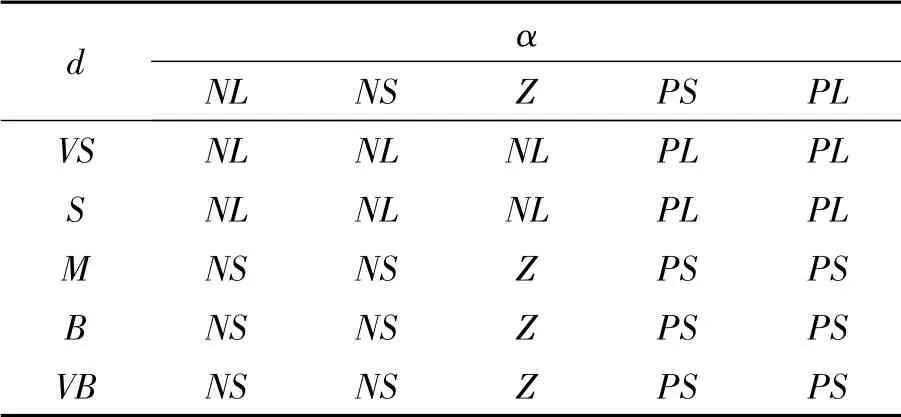
表2 障礙物較大時偏轉角φ 的模糊規則表

模糊推理是是模糊控制器的核心，在此采用Mamdani 推理，用中心面積法去模糊化［11］，最終得到水下機器人所需的偏轉角。

3 仿真研究

3.1 仿真實驗流程

為了驗證所提出的算法能否滿足水下機器人的避障要求，在MATLAB 中進行了仿真實驗。仿真針對的水下機器人以恒速運動，運動步長l =1 mm，分別在障礙物近似為點的情況及障礙物較大且不規則的情況下進行仿真，仿真步驟如圖5所示。在仿真過程中，設計的仿真實驗平臺不僅能夠交互式地任意設置機器人起點和終點位置，還能交互式地任意設置障礙物的數量、大小、形狀和位置，可以更好地檢驗算法的可行性和通用性。

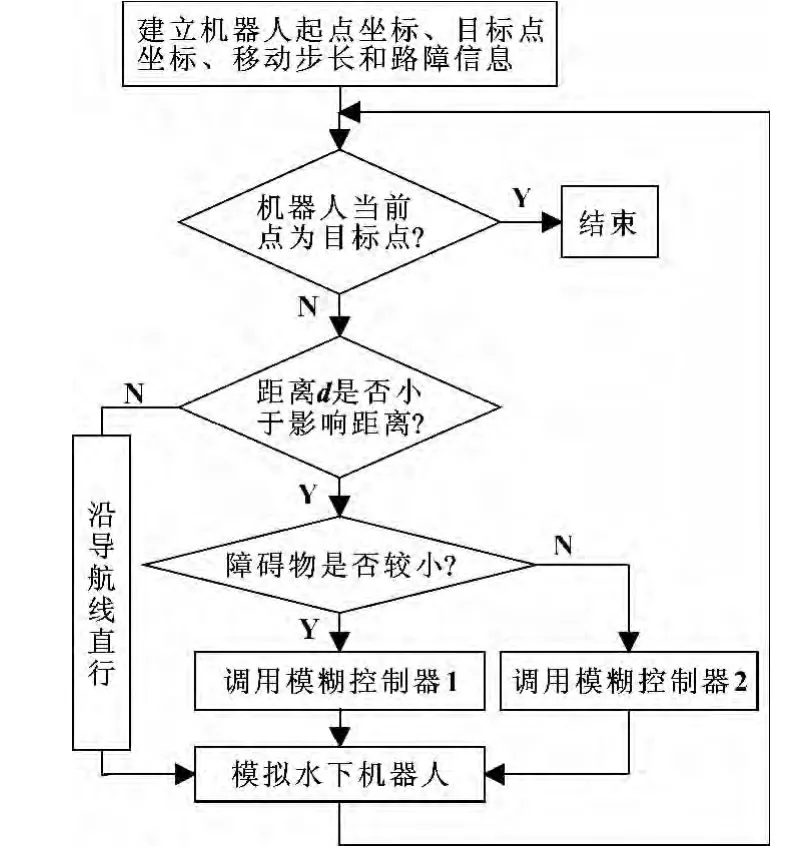
圖5 基于模糊算法的機器人避障流程

3.2 仿真結果分析

通過交互式界面建立機器人起點坐標、目標點坐標、路障信息后，當該障礙物較小時，采用模糊控制器1，對應的模糊控制規則如表1所示。當障礙物對水下機器人的最小影響距離為d=100 mm，輸出偏轉角φ= ［－45°，45°］時，得到圖6 中的路徑1。由于在整個水下機器人避障設計過程中，提出在實現避障功能的同時，能夠盡可能的實現路徑最短且平滑。所以，在仿真過程中，設置障礙物對水下機器人的最小影響距離為d =50 mm，輸出偏轉角φ = ［－20°，20°］時，得出圖6 中的路徑2。經過比較，得知路徑2 明顯優于路徑1，所以根據障礙物的大小，改變模糊控制器的模糊論域，能夠取得更優路徑。

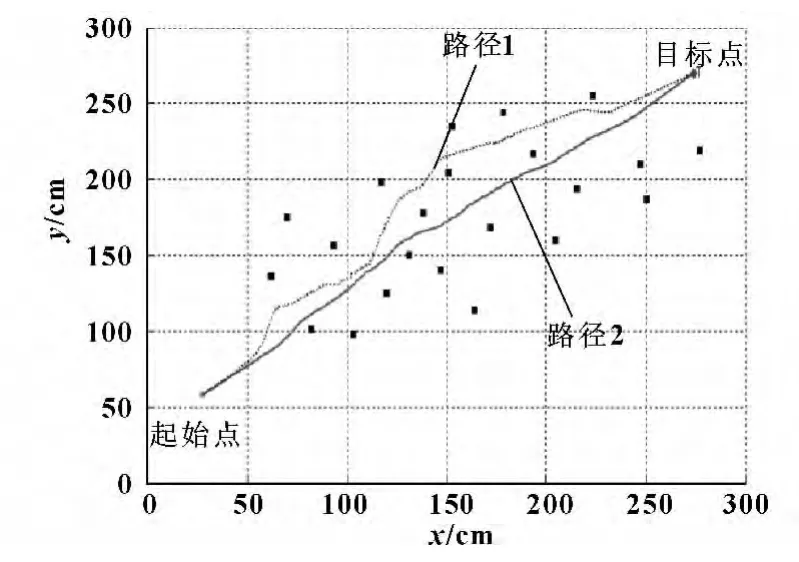
圖6 多點障礙物環境中機器人路徑規劃仿真圖

當障礙物較大時，采用模糊控制器2，對應模糊控制表如表2所示，障礙物對水下機器人的最小影響距離為d=100 mm，輸入偏轉角φ = ［－45°，45°］。首先通過設置多邊形，如圖中* 號節點連線顯示，得到近似轉換的矩形，再通過控制器，得到水下機器人的路徑。通過設置不同路障的數量、位置、大小，機器人的初始位置、目標點位置等信息，檢驗了該算法的可行性，仿真結果如圖7所示。

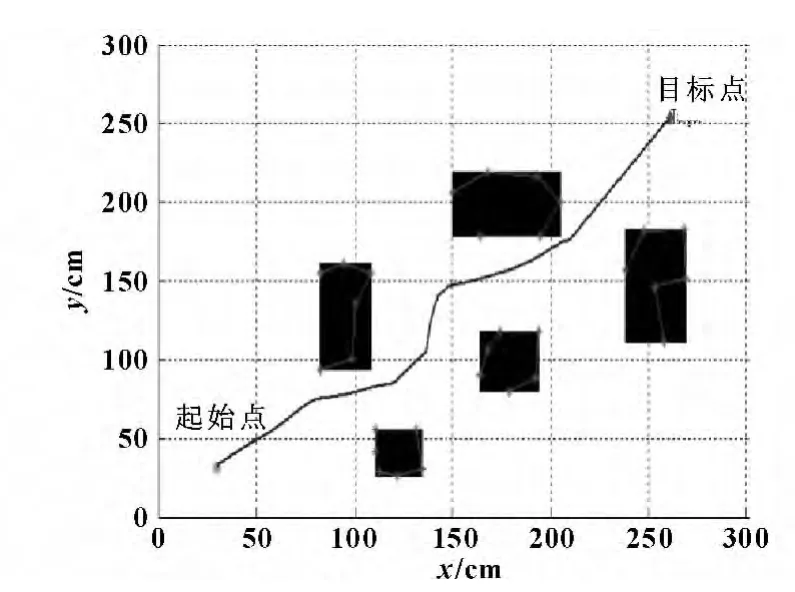
圖7 多矩形障礙物環境中機器人路徑規劃仿真圖

4 結論

由于水下機器人運動環境的復雜性、不確定性，機器人難以完全依照預先規劃的路徑運動。采用測距聲吶、短基線系統等傳感器，實時探測水下未知環境。基于視線導航原理和模糊控制器，實現了水下機器人的避障路徑規劃。此外，根據障礙物的不同尺寸，給出了不同的模糊控制器，可獲得最優化路徑。障礙物不規則時，提取邊緣信息后近似轉換成矩形障礙物，并討論了機器人與矩形障礙物處于不同相對位置時相對距離的求取方式。仿真結果表明:該算法對水下機器人在未知環境中對障礙物的數量、形狀、大小、位置都沒有限制，均可形成一條安全穩定的可靠路徑，驗證了算法的有效性。

【1】郝宗波，洪炳熔.未知環境下基于傳感器的移動機器人路徑規劃［J］.電子學報，2006，34(5):953－956.

【2】高慶吉，雷亞莉，胡丹丹，等.基于自適應感知復位算法的移動機器人定位［J］.電子學報，2007，35(11):2166－2171.

【3】HUQ R，MANN G K I，GOSINE R G.Mobile Robot Uavigation Using Motor Schema and Fuzzy Context Dependent Behavior Modulation ［J］.Applied Soft Computing，2008，8(1):422－436.

【4】崔榮鑫，徐德民，嚴衛生.一種自主水下航行器路徑規劃算法［J］.系統仿真學報，2006，18(12):3373－3376.

【5】陳衛東，朱奇光.基于模糊算法的移動機器人路徑規劃［J］.電子學報，2011(4):971－974.

【6】李曄，劉建成，徐玉如.帶翼水下機器人運動控制的動力學建模［J］.機器人，2005，27(2):128－131.

【7】WU X P，FANG Z P，ZHU J M.Line of Sight Guidance With Intelligent Obstacle Avoidance for Autonomous Underwater Vehicles［C］.OCEANS 2006，Boston，MA，2006:1－6.

【8】李慶春，高軍偉，謝廣明.基于模糊控制的仿生機器魚避障算法［J］.兵工自動化，2011，30(12):65－69.

【9】PETILLOT Y，TEMA R I，LAME D M.Underwater Vehicle Obstacle Avoidance and Path Planning Using a Multi-Beam forward Looking Sonar［J］.IEEE Journal of Oceanic Engineering，2001，26(2):240－251.

【10】WANG L X.Adaptive Fuzzy System and Control:Design and Stability Analysis［M］.Englewood Cliffs:PTR Prentice Hall，1994.

【11】謝超平，孔峰，陶金.基于模糊控制的仿生機器魚轉向控制研究［J］.機器人技術與應用，2009(4):26－27.