機器人運動學逆解及奇異和多解的處理

葉上高，劉電霆

(桂林理工大學機械與控制工程學院，廣西桂林541004)

機器人運動學逆解，即根據工具坐標系相對于基坐標系的目標位姿，求解機器人各關節角。逆運動學在機器人學中占有非常重要的地位，是機器人軌跡規劃和運動控制的基礎，直接影響著控制的快速性與準確性［1］。一般機器人運動學逆解算法可分為以下幾種［2］:解析法(又稱反變換法)、幾何法和數值解法。由PAUL 等提出的反變換法求解過程直觀，因而被廣泛采納，但其求解過程中需多次進行齊次變換矩陣的逆運算和4 ×4 維矩陣的乘積運算，導致求解過程復雜耗時［3］。

大多數工業機器人的幾何結構都滿足Pieper 準則［4］，即3 個相鄰關節軸交于一點或相互平行，其運動學逆解可以得到數量一定的若干組封閉解。對于最后3 個關節為旋轉關節而且軸線相交于一點的六自由度機器人，其前3 個關節決定末端執行器的位置，后3 個關節決定末端執行器的姿態［5］。故文中以其中的典型代表——ABB 公司的IRB2600 機器人為研究對象，提出了一種有別于傳統方法的位姿分離逆解算法，根據末端執行器的位置矢量計算前3 個關節變量，利用末端執行器的旋轉矩陣計算后3 個關節角。此算法逆解過程完全避免了矩陣求逆和4 ×4 維矩陣相乘的運算，過程直觀，因此，比一般的解析算法更加簡單高效，便于實時控制。此外，文中對逆解所涉及的奇異和多解問題的處理也進行了詳細分析。最后，用ADAMS 對該逆解算法的正確性進行了仿真驗證。

1 運動學正解

IRB2600 為6R 機構，采用D-H 方法［6］，建立連桿坐標系如圖1所示。

圖1 IRB2600 機器人的連桿坐標系

IRB2600 機器人的D-H 參數如表1所示。

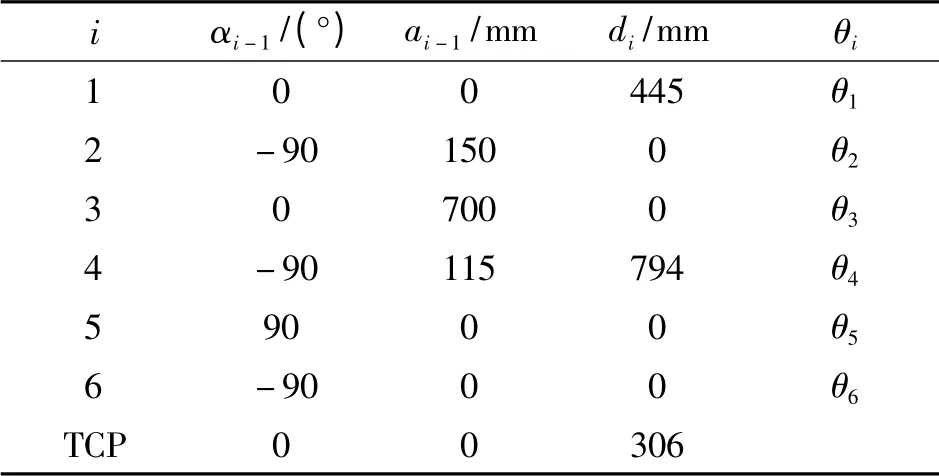
表1 IRB2600 機器人的D-H 參數

由此求得各連桿變換矩陣后連乘得機器人腕點的齊次變換矩陣

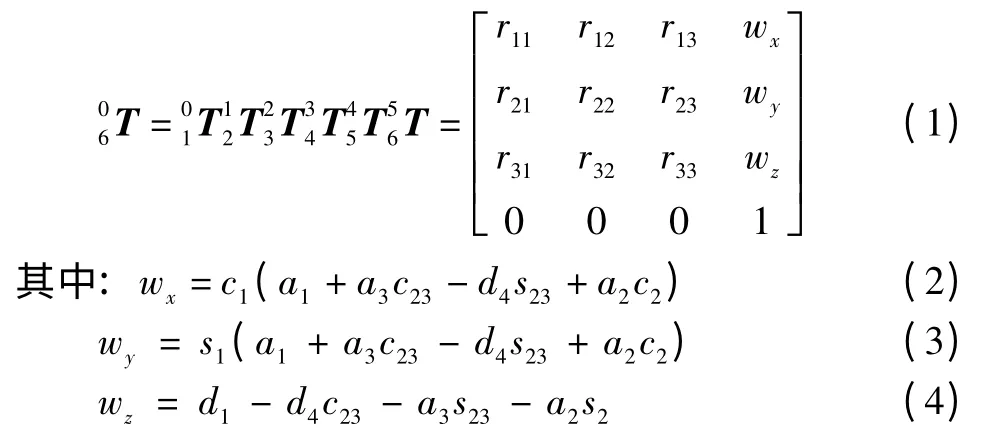
2 運動學逆解算法

2.1 前3 個關節角

求θ1。因a1+a3c23－d4s23+a2c2正負未定，故由式(2)、(3)求得θ1有兩個可能解

θ1A=arctan2(wy，wx)，θ1B=arctan2(－wy，－wx)

求θ2。若c1≠0，由式(2)、(4)整理得

將式(6)和(7)等號兩邊平方后取和，整理得

若c1=0，為避免分母為0，則改用式(3)、(4)用同樣的方法求解。

求θ3。若c1≠0，因θ1和θ2已求得，則由式(2)、(4)整理所得的式(6)、(7)兩式等號左邊已知，即式(6)和(7)構成二元一次方程組，可解得未知數為

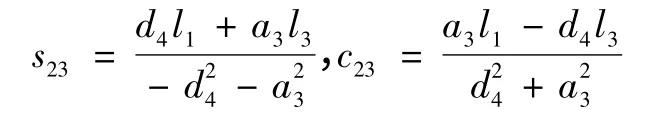
其中:l1=k1－a2c2，l3=k3+a2s2

故θ3=Atan2(s23，c23)－θ2。若c1=0，為避免分母為0，則改用式(3)、(4)用同樣方法求解。

2.2 后3 個關節角

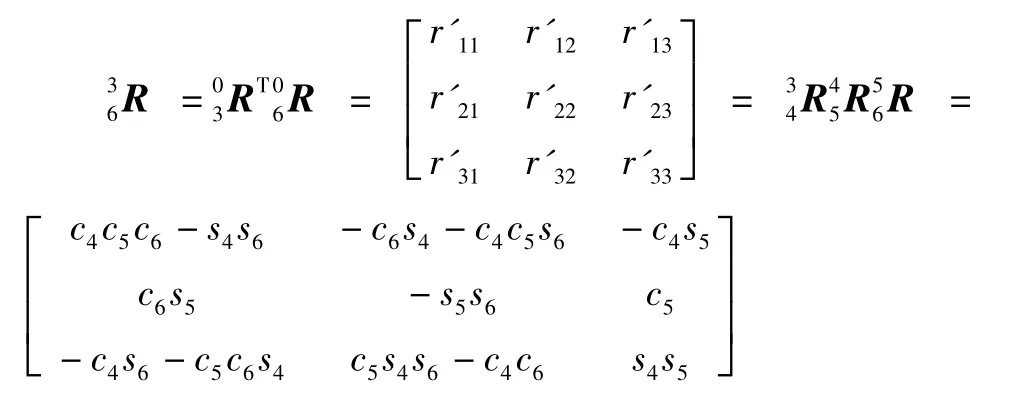
因前3 個角和式(5)已求得，故上式等號左邊已知。

求θ5。由c5=r'23得

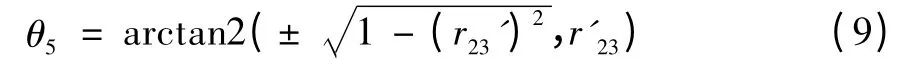
求θ4。由－c4s5=r'13及s4s5=r'33，得

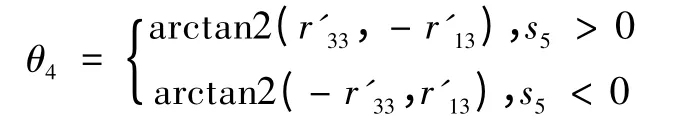
求θ6。由c6s5= r'21及－ s5s6= r'22，用與θ4相同的方法求取。

3 奇異點

若式(1)中wx和wy都為0，則θ1的變化不影響腕點的位置，故為奇異點。若式(8)算出的θ2的兩個可能解相等，則連桿坐標系原點連線O2O3與O3O4共線，故為奇異點。若式(9)解得θ5為零，則關節4 和6 的轉軸共線，故為奇異點［7］。

4 逆解中多解問題的處理步驟

逆解可能存在多解，而機器人的控制需要唯一的確切解。若不考慮避障要求，可按如下步驟獲取唯一最優解。首先，若關節角的求解表達式的值域不能完全包含該關節運動范圍，則在必要情況下，需將求得的關節角可能解加減360°，補出關節運動范圍內的其他可能解［8］;其次，剔除關節運動范圍以外的可能解;最后，由運動連續性［9］，選取與該關節角上一時刻的值距離最近的可能解為唯一最優解。各關節角的求解順序為:先確定θ1的唯一最優解，再利用θ1的最優解按前述逆解方法和多解處理步驟求取θ2的最優解。其余關節角的求取順序依此類推。最后所得的這組唯一的最優關節角即可作為實現機器人目標位姿的控制依據。

表2 IRB2600 機器人的關節活動范圍

5 算法仿真驗證

在ADAMS 中建立IRB2600 機器人模型進行逆解算法的仿真驗證。保持不變，使TCP 在t∈［0，40］沿螺旋線x =944 +400cost，y=－400sint，z=1 354－20t 運動，在t∈(40，50］從該螺旋線終點沿直線回到螺旋線起點。t =0 時刻關節角初始值為θ1=0，θ2=－0.988 6 rad，θ3=－1.178 rad，θ4=0，θ5=1.381 1 rad，θ6=0 rad。ADAMS 仿真過程中關節角的測量結果為圖2 中的實線，用文中方法逆解所得關節角變化曲線在圖2 中用叉號表示。由圖2 可見逆解結果與仿真結果完全重合，證明該算法正確有效。仿真過程中t =40 s 時刻的截圖見圖3。

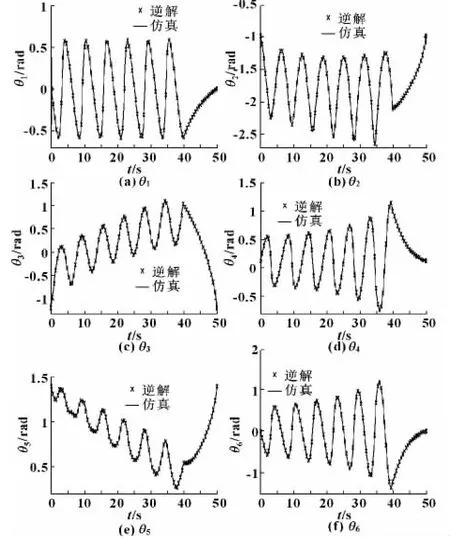
圖2 逆解結果與仿真結果對照圖

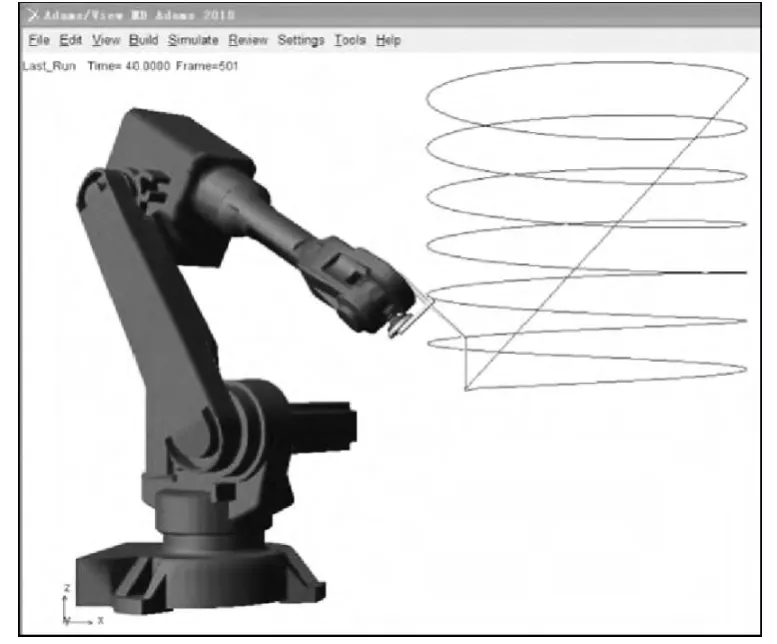
圖3 仿真過程中t=40 s 時刻的截圖

6 結論

仿真證明文中提出的逆解算法正確有效。逆解過程比一般的解析算法更加簡單高效，便于實時控制，對其他機器人的逆解也具有一定參考意義。

【1】劉華山，朱世強，吳劍波，等.基于奇異攝動理論的輸入有界機器人軌跡跟蹤控制［J］.控制理論與應用，2009，26(12):1371－1377.

【2】王其軍，杜建軍.MOTOMAN 機器人逆運動學新分析［J］.哈爾濱工業大學學報，2010，42(3):451－454.

【3】PAUL R P.Robot Manipulators:Mathematics，Programming，andControl［M］.Cambridge:MIT Press，1981.

【4】PAUL R P，SHINANO B E.Kinematical Control Equations for SimpleManipulators［J］.IEEE Trans SMC，1981，11(6):449－455.

【5】GOLDENBERG A A，BENHABIB B，FENTON R G.A Complete Generalized Solution to the Inverse Kinematics of Robots［J］.IEEE Journal of Robotics and Automation，1985，1(1):14－20.

【6】JORGE Angeles.Fundamentals of Robotic Mechanical Systems［M］.New York:Spriger-Verlag，2003.

【7】楊武，蔣梁中.排爆機器人機械手運動規劃［J］.機械設計與制造，2008(5):184－186.

【8】劉華山，朱世強，吳劍波，等.基于向量內積的機器人實時逆解算法［J］.農業機械學報，2009，40(6):212－216，207.

【9】胡杰，張鐵.SCARA 機器人控制系統的設計與研究［J］.機械設計與制造，2012(5):162－163.