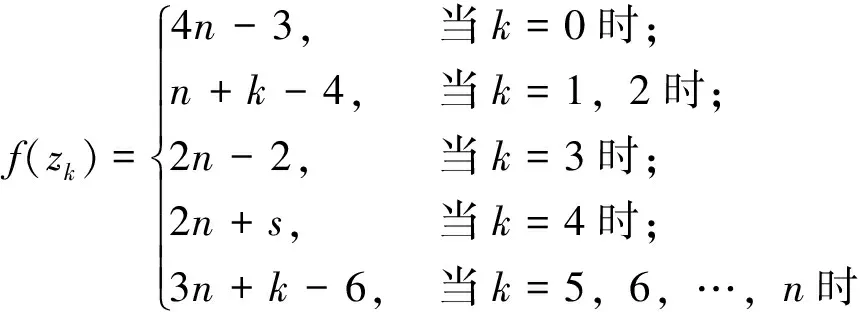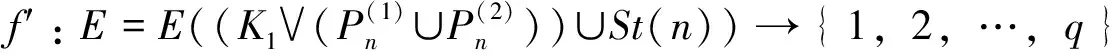非連通圖及的優美性*

孫彩云, 王 濤

(華北科技學院，河北 三河 065201)

圖的標號問題起始于1966年Rosa的著名的優美樹猜想。圖的標號問題是組合數學的熱門課題之一，它不僅屬于圖論領域，也屬于設計理論范疇。圖的優美標號問題在編碼設計、通訊網絡及雷達脈沖等領域有著重要應用[1-4]。近年來，對連通圖及非連通圖的優美性問題研究都受到關注[5-10]。本文給出了兩類非連通圖優美性的證明。

以下所討論的圖G(V,E)均為簡單無向圖，設V=V(G)為圖G的頂點集，E=E(G)為圖G的邊集，|A|為集合A的階數，[a]為不超過實數a的最大整數。

定義1 設圖G=(V,E)，如果對于每一個v∈V，存在一個非負整數f(v)(稱為頂點V的標號)，且滿足：

(i)?u,v∈V，如果u≠v，則f(u)≠f(v)；

(ii) max{f(v)|v∈V}=|E|；

(iii) ?u1v1,u2v2∈E，若u1v1≠u2v2，則f′(u1v1)≠f′(u2v2)， 其中，f′(u1v1)=|f(u1)-f(v1)|。則稱圖G是優美圖，f是G的一個優美標號。

由定義知：如果G是優美圖，則V(G)→{0,1,2,…,|E|}是一個單射；E(G)→{1,2,…,|E|}是一個雙射。

① 當n為偶數時，n=2s=a，b=n-1，

令f(x0)=0，f(x1)=s，

令f(yj)=

f(ya)=2s；

令f(z1)=s-1，f(z2)=4n-s-3，

f(zk)=

其中，f(z3)=f(z2)-(2s-1)=4n-3s-2

=2n+s-2，

f(z4)=f(z3)+(2s-2)=

f(z2)-(2s-1)+(2s-2)=f(z2)-1,

f(z5)=f(z4)-(2s-3)=f(z2)-(2s-2),

f(zn)=f(zn-1)+1；

(i)由于f(x0)

f′(x0x1)=s，f′(x1x2)=5n-s-3，f′(xixi+1)=4n-i-2(i=2,3,…,n-1)，

f′(yjyj+1)=3n-j-3(j=1,2,3,…,n-2)，

f′(x0yj)=

f′(x0ya)=2s=n

f′(yn-2yn-1)=2n-1；

f′(z1z2)=4n-s-3-(s-1)=3n-2，

f′(zkzk+1)=

其中f′(zn-1zn)=1，從而

f′(zn-1zn)

f′(x0x1)

f′(x0ya)

f′(x2x3)

f′(yn-2yn-1)

f′(yn-1yn)

…

f′(x0y1)

f′(x0xa-2)<…

②當n為奇數時，n=2s+1=a+1，n=b，

令f(x0)=0，f(x1)=s，

令f(yj)=

令f(z1)=4n-s-4，f(z2)=s-1，f(z3)=2n+s-2,

f(zk)=

其中，f(z4)=f(z3)+(2s-1)=2n+3s-3，

f(z5)=f(z3)+1,f(z6)=f(z3)+2s-2,

f(zn)=f(zn-1)-1；

(i)由于f(x0)

f′(x0yj)=

f′(x0yb)=f′(x0yn)=2s,f′(yayb)=5n-4s-3,

f′(yjyj+1)=3n-j-2(j=2,3,…,n-2)，

其中f′(x0y1)=n+s，f′(x0ya)=5n-2s-3，

f′(y1y2)=4n-2s+4，f′(yn-2yn-1)=2n；

f′(z1z2)=4n-2s-3，f′(z2z3)=2n-1,

f′(zkzk+1)=

這就是《老人與海》最富哲理的人物語言，也是小說想要揭示的主題。主人公桑提亞哥很“背運”，連續84天沒有捕到魚。他是“背運”，但他不屈服，努力戰勝困難，他是一個勝利者，一個敢于挑戰自己的勝利者。

圖1 優美標號

① 當n為偶數時，n=2s=a，b=n-1，

令f(x0)=0，

其中，f(xa)=5n-1-s，f(xb)=2n-s-1

令f(yj)=

其中，f(yb)=4n-1，f(ya)=2n-1；

令f(z0)=4n-2,f(z1)=n-1，f(zk)=3n+k-3,k=2,3,…,n。

f′(xixi+1)=4n-i-1(i=1,2,3,…,n-1)，

f′(yjyj+1)=3n-j-1(j=1,2,3,…,n-1)，

f′(x0yj)=

f′(z0z1)=3n-1，f′(z0zk)=n-k+1，(k=2,3,…,n)

從而

f′(z0zn)

② 當n為奇數時，n=2s+1=a+1，n=b，

令f(x0)=0，f(x1)=1，f(x2)=5n-2，

其中，f(xa)=n+s-3，f(xb)=4n+s-2；

令

其中，f(ya)=4n-2，f(yb-2)=2n-3，

其中，f(zn)=f(zb)=4n-b；

(i)由于f(x0)

f′(x0x1)=1，f′(x1x2)=5n-3，f′(x2x3)=2，

f′(xixi+1)=4n-i(i=3,…,n-1)，

其中，f′(x0yb)=f′(x0yn)=2n；

f′(yjyj+1)=3n-j-1 (j=1,2,3,…,n-2)，f′(yn-1yn)=2n-2；

從而

圖2 優美標號

參考文獻：

[1]MA K J. Graceful graph [M]. Beijing：Peking University Press, 1991．

[2]ACHARYA B D，HEGED S M. Arithmetic graphs[J].J Gragh Theory, 1990, 14(3):275-299.

[3]MARTIN GARDNER. Mathematical games [J]. Scientific American, 1972, 22(6): 625-645.

[4]ECKIER A R. The construction of missile guidance codes resistant to random interference [J]. Bell Syst Technical J, 1960, 39: 973-994.

[5]劉瑞芹，張昆龍．非連通并圖的優美標號研究[J]．合肥工業大學學報：自然科學版, 2009, 32(6): 940-944．

[7]王濤，李德明．和輪相關圖的優美性[J]. 中山大學學報：自然科學版, 2011, 50(6): 16-19．

[9]魏麗俠，賈治中．非連通圖G1 UG2及G1 UG2 UK2的優美性[J]. 應用數學學報, 2005, 28(4): 689-694．