基于AR模型的水電機組振動信號趨勢預測
孫慧芳,付婧,鄭云峰
(中國水利水電科學研究院,北京 100038)
水電機組是水電能源的關鍵設備,機組運行狀況的好壞直接影響水電站的安全運行。目前,水電機組正朝著高水頭、高效率、高轉速和大容量的方向發展,隨著狀態監測與故障診斷技術水平的發展,以及設備管理水平的提高,水電站設備的維修理念以“預防為主,計劃檢修”的方針開始嘗試轉變為“預測性維修”的檢修模式。由于水電機組的故障信息大部分都通過振動信號來反映,因此對水電機組的振動信號進行趨勢預測很有必要。
對振動信號的趨勢預測是根據其過去和現在的情況,科學地預測和推斷這些信號未來的發展趨勢。趨勢預測方法一般以時間序列進行數據建模,基本思想是將一列隨時間變化又互相關聯的數據用相應的數學模型加以近似描述,實現最小方差下的最佳預測。文章對某電站上機架+X向的一段振動數據進行了基于AR模型的趨勢預測,計算方法簡單,可以滿足現場實時性的需求。
1 ARMA模型
時間序列xtΣΣ可以表示為n階自回歸m階滑動平均混合時序模型,即ARMA(n,m)模型,表達式如下:
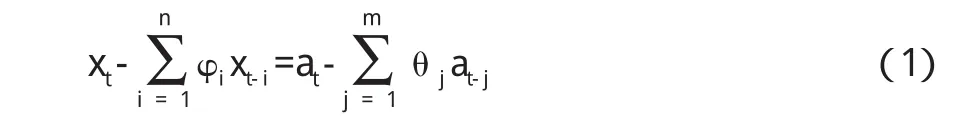
式中,xt為Σ在t時刻的取值;為自回歸(Auto-Regressive)參數;θ1=(1,2,……m)為移動平均(Moving Average)參數;at是均值為0,方差為的獨立正態分布序列(白噪聲)。當n=0時,模型稱為純滑動平均模型MA(m);當m=0時,模型成為純自回歸模型AR(n)。
由于水電機組的振動復雜性,振動信號一般是非平穩的時間序列,需要經過適當的變換得到平穩的時間序列ARMA(n,m),為此提出了ARIMA模型:將一個非平穩序列進行差分處理得到平穩時間序列。設Σ為非平穩序列,存在正整數d,使得,t>d,其中稱為d階差分算子。ARIMA模型實質上是平穩時間序列分析在非平穩情況下的拓展,但其仍基于ARMA分析。
對于ARMA模型和AR模型之間的關系有wold分解定理:任何一個方差有限的平穩ARMA過程都可以表示為唯一的階數可能無窮大的AR過程。ARMA模型的隨機信號總可以化為一定階數的AR模型,因此AR模型的參數估計在實際問題中應用較廣。
2 AR模型的建模
AR模型的建模包括模型的定階和模型的參數估計,即要估計出自回歸參數φi和模型的階數n。
模型階數估計的一個常用準則為AIC準則,計算公式如下:

AR模型模型參數估計的方法有很多,如:最小二乘估計法、加權算法和Burg算法等等,文章采用Burg算法。Burg算法的基本思想是對信號進行前向和后向的預測,令前后向預測誤差功率之和為最小。MATLAB中有可以實現Burg算法的AR模型參數估計函數[ae]=arburg(xn),其中a為函數返回的模型系數向量,e為最小預測誤差。
參數估計需要預先知道模型階次,因此建模過程中應先給定模型階次,按照Burg算法估計模型參數,可以得到各階模型,最后取最小AIC(n)值對應的階次來確定模型的最佳階此,同時也可以確定AR模型。
3 水電機組振動信號的AR建模
取某電站上機架+X向的2000個振動數據進行建模,其序列圖見圖1所示,可以看出該序列不是平穩序列。對其進行2階差分,差分后數據自相關系數見表1,自相關系數隨著k的增大而逐漸趨向0,證明差分后的序列為平穩時間序列,序列圖見圖2所示。
按照AR模型的建模方法對差分后的振動數據進行建模,使用Burg算法估計出各階參數,然后計算相應的AIC值,不同階數對應的AIC值如圖3所示,從圖中可知,當n=48時AIC值最小,即最佳模型階次為48階。

圖1 上機架+X向振動信號序列圖
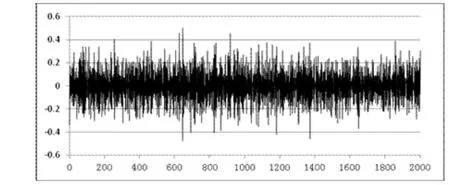
圖2 上機架+X向振動信號差分后的平穩序列

圖3 AR模型在不同階次下的AIC值
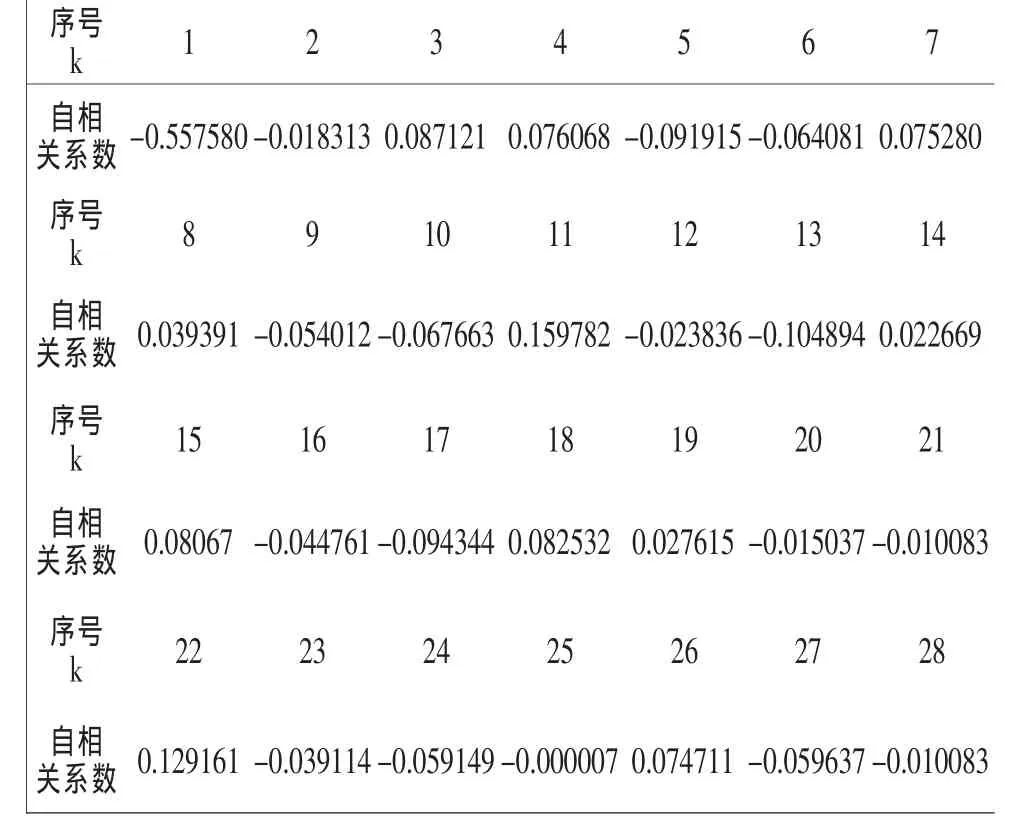
表1 差分后的振動信號自相關系數估計值
以差分后的振動信號數據做AR模型擬合,估算出該平穩信號的估計值,經過相應的反變換得到原始振動信號的擬合模型,并以100個數據作樣本預測,預測結果見圖4所示。由圖4可以看出利用AR模型對水電機組振動信號預測的數據與實際采集到的數據基本一致。
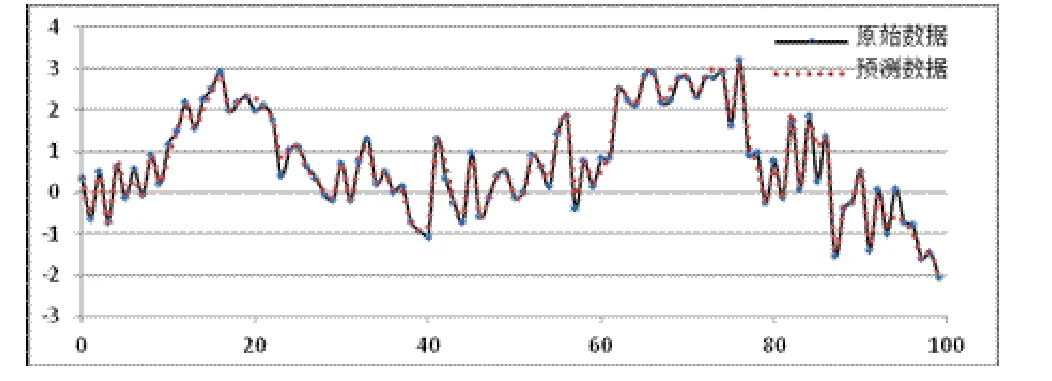
圖4 預測值與實際值的比較
4 結語
上述分析說明采用AR模型對水電機組的振動信號進行趨勢預測是科學的。但是,該方法在計算過程中存在下列問題:由于水電機組的振動信號是隨機的非平穩時間序列,對于個別參數計算過程會經常出現矩陣奇異或近奇異的情形,矩陣求逆可能遇到困難,影響計算精度,因此后續需要對這些問題進行進一步的研究。

