一種基于轉(zhuǎn)矩可達集的操縱面組合分配設(shè)計方法

史靜平, 屈曉波, 畢可軍

(1.西北工業(yè)大學 自動化學院, 陜西 西安 710072; 2.飛行器一體化技術(shù)重點實驗室, 陜西 西安 710072)

先進飛機操縱面的分配設(shè)計[1-2]的含義有2個層面:①確定舵面在不同飛行任務(wù)下的組合方案;②在此基礎(chǔ)上確定匹配的舵面分配算法。目前的研究成果多集中于具體分配算法的研究上,如:早期的偽逆法[3]、加權(quán)偽逆法[4],在此基礎(chǔ)上改進的級聯(lián)廣義逆法[5]、再分配偽逆法[6],以及20世紀90年代中期提出的直接分配法[7]、面搜索法[8]、對邊搜索法[9]、基于數(shù)學規(guī)劃的分配法[10]等。在具體分配算法的研究上取得的理論成果可謂頗豐,但在操縱面組合分配的研究上,成果有限,現(xiàn)有的方法多采用基于數(shù)學規(guī)劃的分配方法,即:針對不同的飛行任務(wù)建立相應(yīng)的舵面分配優(yōu)化指標,采用線性規(guī)劃、二次規(guī)劃等數(shù)學方法進行尋優(yōu)求解,如:基于二次規(guī)劃的多目標分配方法[11]、基于基排序線性規(guī)劃的分配方法[12]等,這些方法雖然在數(shù)學上較好地解決了操縱面組合與分配求解,但工程應(yīng)用仍存在一些亟待解決的問題,例如:①數(shù)學規(guī)劃類方法需要在線尋優(yōu),由于實時性問題難以直接應(yīng)用;②數(shù)學規(guī)劃類方法將所有的舵面放在一起分配,沒有充分考慮舵面的實際物理特性,某些組合方式產(chǎn)生的分配解可能會導致相鄰舵面間產(chǎn)生復雜的氣動耦合效應(yīng),不利于實際控制;③數(shù)學規(guī)劃類方法需要根據(jù)各飛行階段進行模態(tài)切換,這極大地增加了控制系統(tǒng)設(shè)計的復雜度。

針對上述問題,本文提出了一種基于轉(zhuǎn)矩可達集(AMS: Attainable Moment Subset)設(shè)計的操縱面組合分配方法,該方法首先計算出各個基控制組的轉(zhuǎn)矩可達集,在此基礎(chǔ)上綜合分析各個基控制組轉(zhuǎn)矩可達集構(gòu)造特點,結(jié)合雷達反射特性和阻力特性確立一組主控舵面,以使現(xiàn)有常規(guī)布局飛機的控制律設(shè)計方法和經(jīng)驗得以沿用。當主控舵面不能滿足機動飛行對于可用力矩的需求時,啟用其他輔助操縱面及推力矢量操縱面,輔助操縱面的管理按照舵面偏轉(zhuǎn)對于雷達反射的優(yōu)先級進行。隨后的仿真驗證了該方法的有效性。

1 問題的描述

設(shè)飛機期望的力矩向量是v(t)∈R3,操縱面的偏轉(zhuǎn)量為u(t)∈Rm,控制分配就是在給定v(t),及控制效率矩陣B:Rm→R3(m>3)的情況下,求解不定方程:

Bu(t)=v(t)

(1)

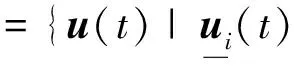
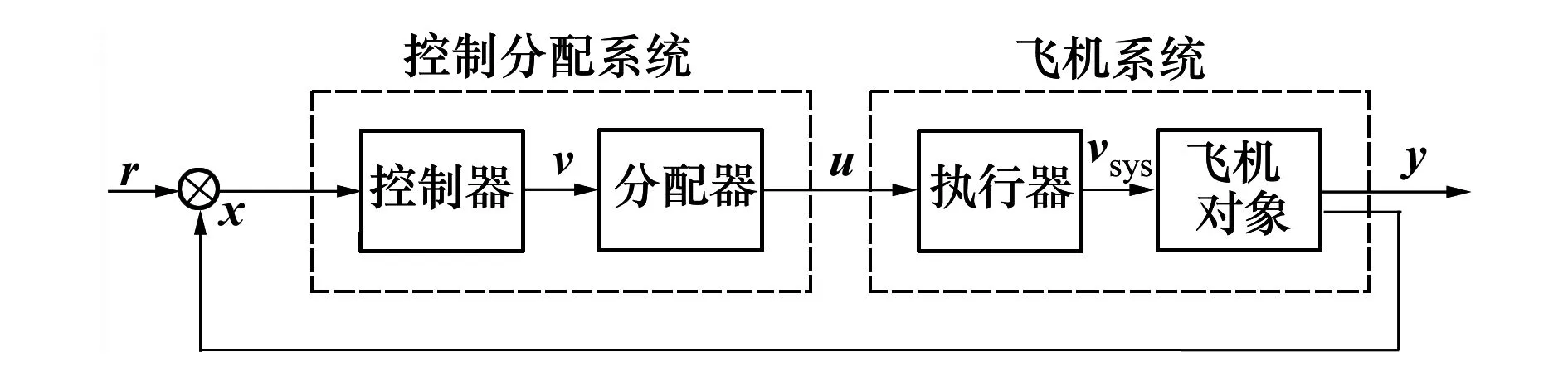
圖1 多操縱面控制系統(tǒng)結(jié)構(gòu)圖

操縱面的控制分配應(yīng)與飛機的飛行任務(wù)相結(jié)合,一般來說,飛機的飛行由起飛/爬升、巡航、突防、大機動飛行、下降/著陸等幾個階段構(gòu)成。在操縱面組合方案設(shè)計時,應(yīng)根據(jù)不同的飛行任務(wù)建立起相應(yīng)的操縱面分配指標。現(xiàn)有的基于數(shù)學規(guī)劃的方法在解決該問題時,所采用的研究思路可概括為如下2個優(yōu)化過程:

,u∈Θ

Θ=argmin‖W(Bu-v)‖p,u∈Ω

這種方法在分配時將所有可用的控制面同時調(diào)動起來,根據(jù)各階段的優(yōu)化指標輸出操縱面偏轉(zhuǎn)量。這種方法在解決多目標分配問題的同時,也帶來了新的問題,即:如何根據(jù)飛機各階段的飛行特點辨識出當下的分配指標。是通過飛行員手動切換,還是通過態(tài)勢感知的原理智能地決策出分配指標,抑或是簡單地將多目標分配問題轉(zhuǎn)化為單目標分配問題取得一個次優(yōu)解。客觀地講,不論是采用哪種方式,對控制系統(tǒng)設(shè)計都帶來了極大的挑戰(zhàn),即便是人工手動切換也增加了操控系統(tǒng)設(shè)計的復雜度。從工程角度看,同時調(diào)用所有控制面參與分配不利于系統(tǒng)的可靠性,各模態(tài)自動切換帶來的難度也增加了控制系統(tǒng)設(shè)計的負擔。此外,不同舵機的速率并不相同,不加以區(qū)別同時調(diào)用也不合理,特別是對于推力矢量等異構(gòu)操縱面更應(yīng)區(qū)別對待。

本質(zhì)上,不論是何種舵面組合方式,都應(yīng)該首先滿足飛機運動對于力矩的需求,在此基礎(chǔ)上使分配解滿足各階段的分配指標。基于這種考慮,本文提出了一種基于轉(zhuǎn)矩可達集設(shè)計的操縱面組合分配方案:首先將操縱面分成若干可行的基控制組,并計算各個基控制組的轉(zhuǎn)矩可達集;然后結(jié)合工程經(jīng)驗選擇具有較大轉(zhuǎn)矩可達集的基控制組作為主控制組,其他舵面作為輔助操縱面,并根據(jù)雷達反射特性對輔助操縱面進行優(yōu)先級排序;在實際飛行時,若主控制組不能滿足飛機對于可用力矩的需求,根據(jù)優(yōu)先級啟用輔助操縱面。

本文的行文流程如下:首先對轉(zhuǎn)矩可達集的求解方法進行研究,然后給出基于轉(zhuǎn)矩可達集設(shè)計的操縱面組合分配方法。

2 轉(zhuǎn)矩可達集的求解

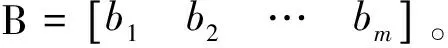
(2)

式中:k≠a,b,c,i,j,分析(2)式的結(jié)構(gòu)可得到如下結(jié)論:

1) 當ui、uj、uk為常值,ua、ub、uc在定義域內(nèi)自由變化時,映射后所形成凸體Φ3為一盒體。

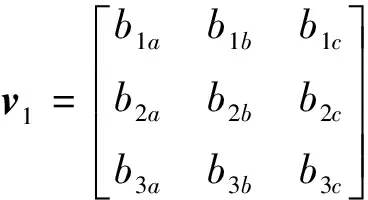
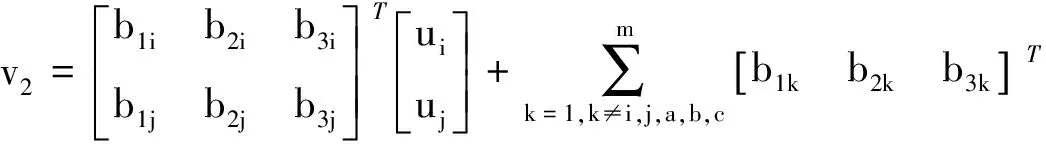
通過上面討論可知:若B的任意3×3子矩陣滿秩,只要允許3個控制變量自由變化,則其形成的集合v1必為凸體。因此在B的任意3×3子矩陣滿秩的情況下,Φ3的平面P只可能是控制向量u的N(N<3)個元素自由變化,其他(m-N)個元素處于常值狀態(tài),具體的:

當N=1,即1個變量自由變化時,rank(v)=1,因此映射v=Bu形成的集合為直線段;

當N=2,即2個變量自由變化時,rank(v)=2,因此映射v=Bu形成的集合為有限的平面。

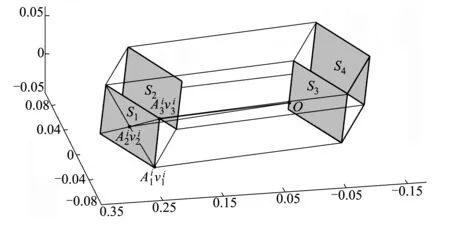
圖2 Φ3的幾何構(gòu)造(m=4)

設(shè)集合ξi,j是u中的元素ui和uj在定義域內(nèi)自由變化,其它元素處于常值時所確定的一組平行平面:

(3)

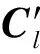
B′(1,i)=0

B′(1,j)=0

(4)

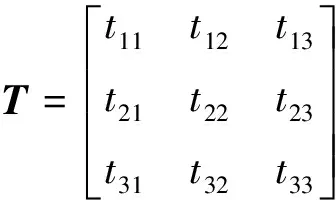
(5)

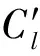
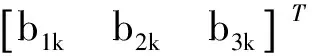
(6)

式中:η為平面ξi,j的法向量:η=bi×bj。設(shè)?(Φ3)的2個外表面為fi,j。當控制量uk取值使Clk極大或極小時所對應(yīng)的平面ξi,j即為Φ3的表面fi,j,因此根據(jù)ηT·bk符號與Clk的取值關(guān)系便可以確定(m-2)個控制量的取值。例如:正向表面fi,j的4個頂點為:

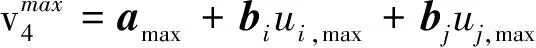
(7)

式中:

μk,max

(8)

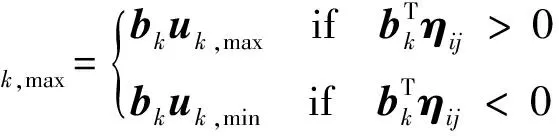
(9)

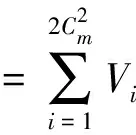
(10)

通過求解Cl、Cm、Cn軸與邊界?(Φ3)的交點,可以獲取飛機在三軸力矩上的跨度。

當控制效率矩陣不滿足任意3×3子矩陣滿秩時,會出現(xiàn)ηT·bk=0的情況。對于此種情況,可通過“小擾動破壞其相關(guān)性”使問題得以求解。

3 基于轉(zhuǎn)矩可達集的操縱面組合分配設(shè)計

戰(zhàn)斗機的飛行一般由起飛/爬升、巡航、突防、大機動飛行、下降/著陸等幾個階段構(gòu)成。為了提高飛機的性能,在控制系統(tǒng)設(shè)計時通常期望操縱面的控制與分配能夠滿足:在超聲速巡航階段,操縱面偏轉(zhuǎn)產(chǎn)生的阻力最小,以減小燃油;在突防階段,操縱面偏轉(zhuǎn)產(chǎn)生的雷達反射最小,以減小威脅;在大機動階段,飛機可用力矩最大,以增加飛機敏捷性。如前文所述,如果對于各飛行階段均建立相應(yīng)的分配模態(tài)進行操縱面分配設(shè)計,將大大增加控制系統(tǒng)設(shè)計的復雜度,并不利于工程實際的應(yīng)用。

事實上,目前歐美先進戰(zhàn)斗機的主控舵面與輔助操縱面的區(qū)別依然是較為明顯的。例如:美國第四代戰(zhàn)斗機F-22雖然擁有12個可控舵面,但通常情況下仍然僅利用升降舵、方向舵和副翼3個主操縱面控制飛機運動,其他舵面僅在主控舵面氣動效能不足時使用,如:過失速機動、主控舵面損傷時,而對于舵面雷達反射特性和超巡阻力特性的考慮,主要是在翼型設(shè)計、氣動布局設(shè)計時完成的;俄羅斯的三翼面布局飛機Su-30MKI和Su-33,它的主控舵面也由升降舵、副翼和方向舵構(gòu)成,鴨翼(小翼)主要起到增升和增大可用迎角的作用。就目前飛行器發(fā)展的現(xiàn)狀而言,操縱面的控制分配設(shè)計不能忽略舵面間的區(qū)別而簡單地進行純粹數(shù)學意義上的組合與分配。在對多操縱面布局飛機的控制系統(tǒng)進行設(shè)計時,仍應(yīng)首先確定一組主控舵面,以使現(xiàn)有常規(guī)布局飛機的控制律設(shè)計方法和經(jīng)驗仍然得以沿用。當主控操縱面不能滿足飛機機動飛行對于力矩的需求時,啟用輔助操縱面或推力矢量操縱面;對于輔助操縱面的調(diào)度與管理可按照舵面對于雷達的反射特性和阻力特性進行。

根據(jù)上述思想,本文給出了一種基于轉(zhuǎn)矩可達集的操縱面分配設(shè)計方法。由于多操縱面控制分配有2個主要的任務(wù)：①合理的組合多種控制面,使飛機能夠適應(yīng)不同的飛行任務(wù)和飛行條件;②在控制面發(fā)生故障的情況下仍然能通過剩余控制面的重新組合[13]來協(xié)同控制飛機運動,從而提高飛機對故障及損傷的魯棒性。因此,本文提出的方法也兼顧考慮了操縱面故障時的分配情況。為了描述該過程,首先引入基控制組和控制效率基的概念[12]。

定義對于某個分配系統(tǒng),若其任意n(m≥n≥3)個操縱面ui=[u1,u2,…,un]的控制效率向量(b1,b2,…,bn)之間線性無關(guān),則稱該組操縱面ui為分配系統(tǒng)的一個基控制組,將其效率向量構(gòu)成的組合Bbase=[b1,b2,…,bn]稱為該基控制組的效率基。

根據(jù)該定義,對于任意3×3子矩陣滿秩的分配系統(tǒng),它的任意3個操縱面都可構(gòu)成一個基控制組,每個基控制組均能夠為飛機提供三軸力矩。多操縱面布局飛機的基控制組是不唯一的,我們可以通過計算基控制組的轉(zhuǎn)矩可達集對基控制組的效能進行評價。基控制組的轉(zhuǎn)矩可達集體積越大,則其可提供的力矩效能越高。

主操縱面應(yīng)具備控制飛機完成大部分機動飛行的能力,因此主操縱面應(yīng)具備較好的氣動特性,其控制效率向量構(gòu)成的效率基應(yīng)具有較大的轉(zhuǎn)矩可達集,這樣也可以避免輔助操縱面、推力矢量操縱面頻繁的調(diào)度,進而降低發(fā)動機的維護費用。本文提出的基于轉(zhuǎn)矩可達集的操縱面組合分配方法具體設(shè)計步驟如下:

1) 首先將推力矢量操縱面之外的(m-3)個操縱面進行組合,選出線性無關(guān)的多個基控制組。

2) 分別計算各個基控制組對應(yīng)的轉(zhuǎn)矩可達集體積,并將其按大小排序。

3) 對排好序的各個基控制組進行比較,綜合考察各組舵面的阻力、升力和雷達反射特性,結(jié)合工程經(jīng)驗選擇具有較大轉(zhuǎn)矩可達集的基控制組作為主控操縱面。其余的基控制組按轉(zhuǎn)矩可達集體積大小進行優(yōu)先級排序,作為備用控制組,當主控制組發(fā)生故障時使用。

4) 將主操縱面列表之外的操縱面作為輔助操縱面,當主操縱面控制組不能滿足飛機大機動飛行對于力矩的需求時,啟用輔助操縱面;當輔助操縱面也不能滿足需求時,啟用推力矢量操縱面。

5) 啟用輔助操縱面時,飛機通常處于突防或大機動狀態(tài),因此對于輔助操縱面的調(diào)度與管理按照舵面對于雷達反射的優(yōu)先級進行。

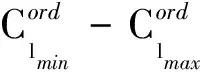
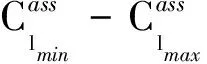
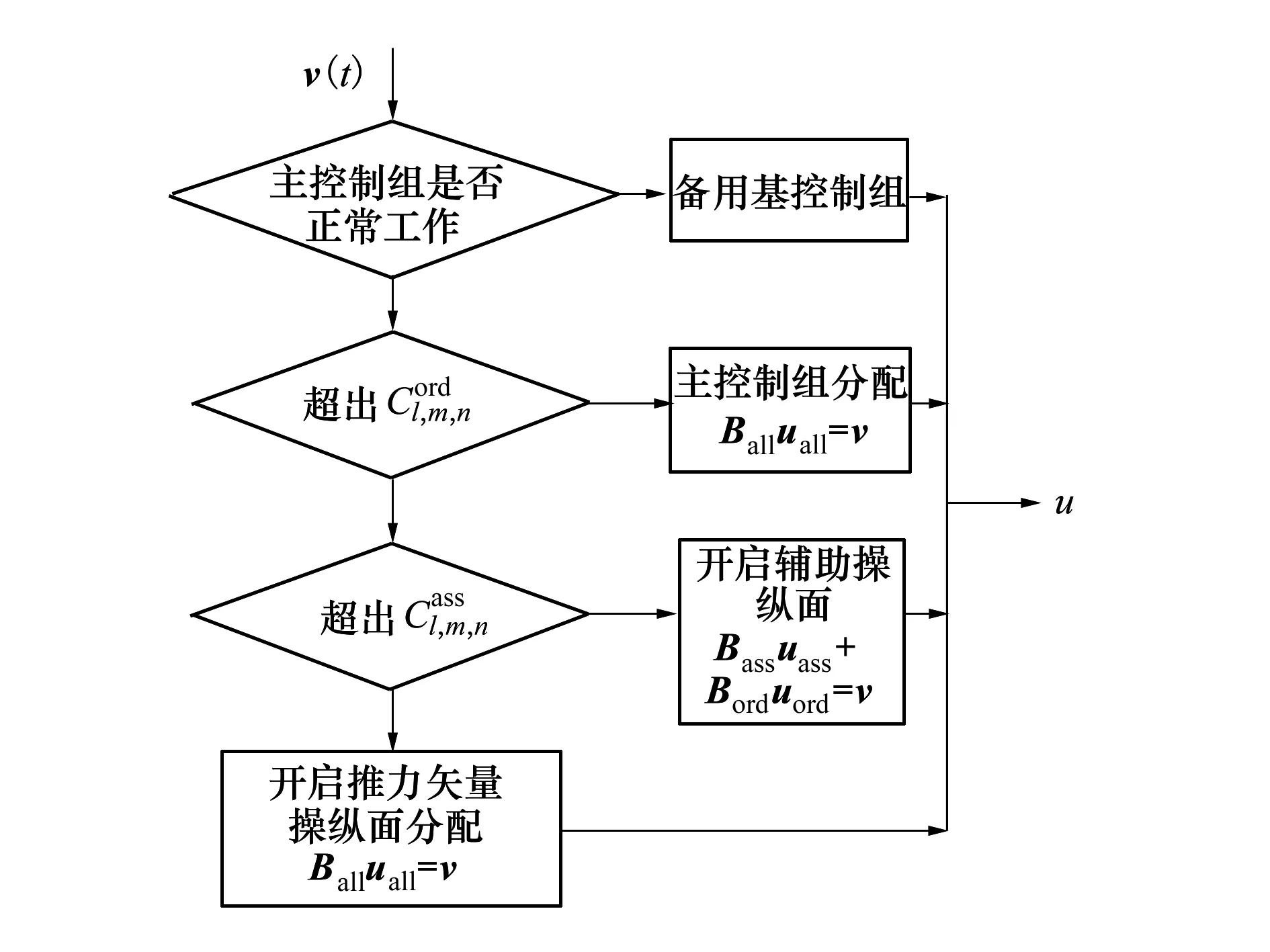
圖3 操縱面分配結(jié)構(gòu)示意圖

通過對三軸可用力矩的監(jiān)測,該方法實現(xiàn)了對于舵面調(diào)度的分配與管理,同時也兼顧考慮了舵面分配對于隱身能力的影響,并實現(xiàn)了舵面故障情況下的重構(gòu)控制。

此外,飛機在起飛/著陸階段要求具備較好的升力特性,這一階段目前主要依賴飛行員手動操縱襟翼來提高飛機的升力。文獻[13]中介紹了一種先進布局飛機的分配方案,其分配方案的切換與飛行任務(wù)的內(nèi)容、迎角的大小等因素相關(guān)聯(lián)。如何根據(jù)飛機的飛行狀態(tài)和任務(wù)自動切換分配模式仍然有待進一步的深入研究。

4 仿真驗證

某飛機在30 000 ft,0.3Ma,a=12.5°時的控制效率矩陣B為:

B陣的3行分別為各操縱面的滾轉(zhuǎn)操縱效率值、俯仰操縱效率值、偏航操縱效率值。三軸力矩與操縱面偏轉(zhuǎn)角的關(guān)系滿足線性假設(shè):

Bu=v

各操縱面的位置限制如表1所示。其中,操縱面u1、u2為右、左升降舵的偏轉(zhuǎn)角,u3、u4為右、左副翼的偏轉(zhuǎn)角,u5為方向舵的偏轉(zhuǎn)角,u6、u7為右、左前緣襟翼,u8、u9、u10分別為矢量發(fā)動機在滾轉(zhuǎn)、俯仰、偏航方向的偏轉(zhuǎn)角。

表1 操縱面位置限制

為了對該飛機進行操縱面分配設(shè)計,首先確定其主控制組,將可能的基控制組列表如下:

表2 基控制組構(gòu)成

計算上述基控制組轉(zhuǎn)矩可達集的體積,以及三軸力矩與轉(zhuǎn)矩可達集的交點,列表如下:

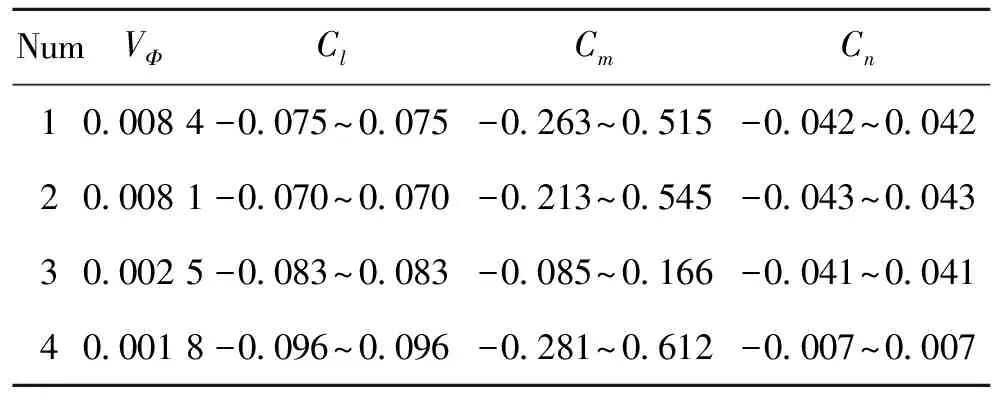
表3 基控制組可達力矩集構(gòu)成

從表3可以看出,1號、2號基控制組均取得了較大的轉(zhuǎn)矩可達集,1號基控制組與2號基控制組的區(qū)別在于:1號基控制組能夠取得更大的低頭力矩,而2號基控制組能夠取得更大的抬頭力矩。3號、4號基控制組的轉(zhuǎn)矩可達集雖然較小,但能夠獲得較大的滾轉(zhuǎn)力矩。

從隱身能力上來看,飛機的前緣襟翼橫跨整個機翼前緣,當其發(fā)生角度變化時,與機翼產(chǎn)生的凹腔結(jié)構(gòu),將導致雷達反射大大增強,因此前緣襟翼作為常規(guī)控制面不利于隱身。綜合考慮各個基控制組的優(yōu)缺點,選擇具有最大轉(zhuǎn)矩可達集體積的1號基控制組(升降舵+副翼+方向舵)作為主控制組,2號、3號和4號控制組按優(yōu)先級排序作為備用控制組。當副翼發(fā)生故障時,采用2號控制組;當升降舵發(fā)生故障時采用3號控制組;當方向舵發(fā)生故障時采用4號控制組。從表3還可以看出,方向舵對飛機航向的作用非常顯著,沒有方向舵參與航向控制時,僅能取得0.001 8的轉(zhuǎn)矩可達集,此時Cn跨度僅為-0.007～0.007。

圖4 包含輔助操縱面的轉(zhuǎn)矩可達集結(jié)構(gòu)圖

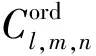
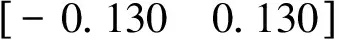
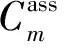
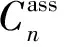
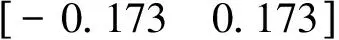
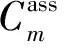
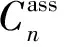
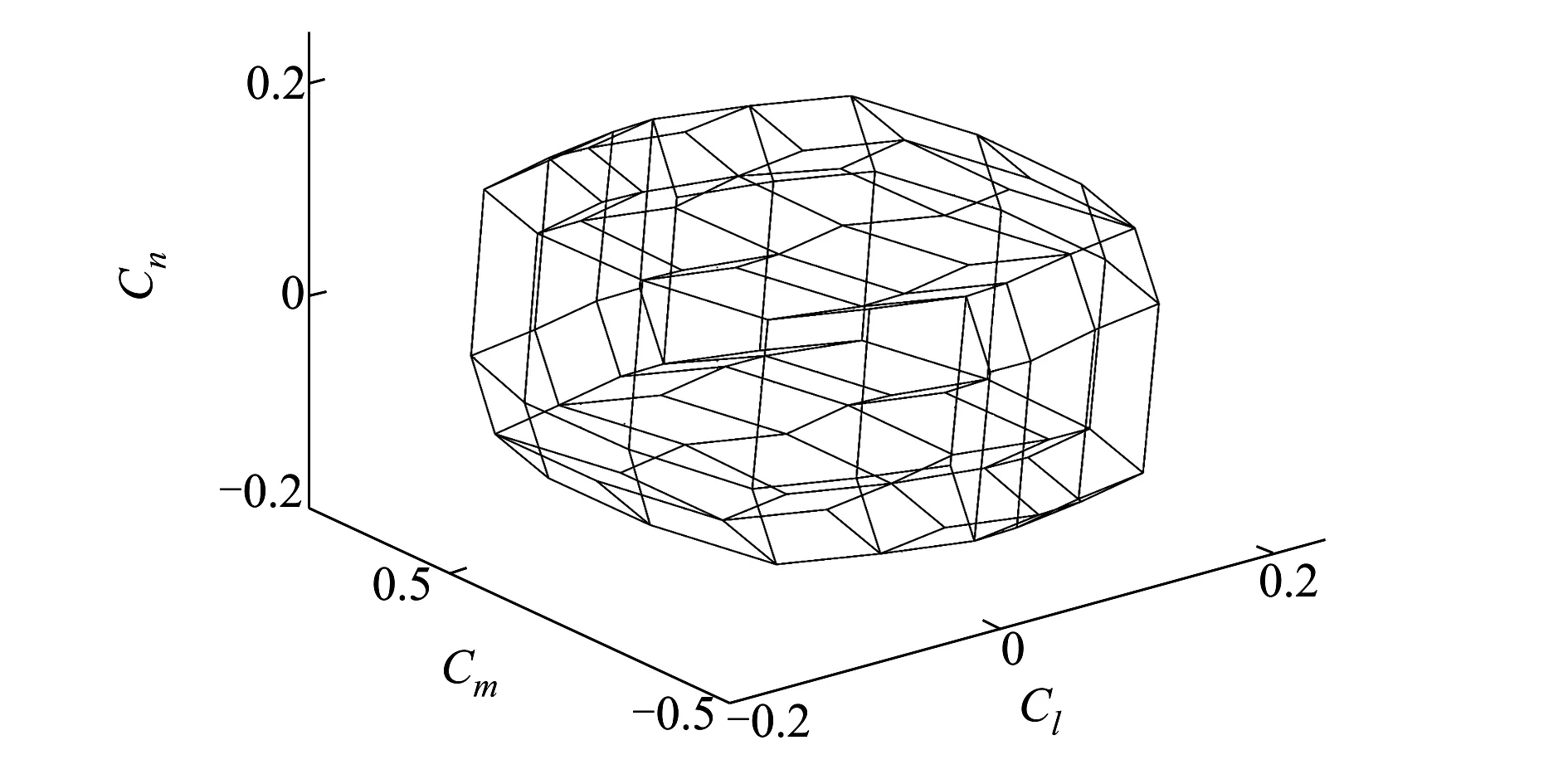
圖5 分配系統(tǒng)AMS幾何構(gòu)造

根據(jù)AMS的幾何構(gòu)造,我們可以計算出在給定期望力矩時,操縱面的的分配情況。例如當期望力矩v=[0.164 5,-0.020 2,-0.127 2]T時:

1) 若僅使用主控制組,在該矢量方向所能取得的最大力矩為:v=[0.059 3,0.007 3,-0.045 8]T,對應(yīng)的控制量為

2) 若加入襟翼,則在該矢量方向所能取得的最大力矩為v=[0.060 8,0.007 5,-0.047 0]T,對應(yīng)的控制量為

3) 若加入推力矢量操縱面,則可實現(xiàn)對期望力矩的完全分配,此時對應(yīng)的控制量為:

5 結(jié) 論

本文首先對轉(zhuǎn)矩可達集的求解進行了研究,通過分析轉(zhuǎn)矩可達集的幾何構(gòu)造,對求解中的幾個難點進行了詳細解釋,并推導了轉(zhuǎn)矩可達集的計算公式。通過探討先進戰(zhàn)斗機各飛行階段對于操縱面分配的要求,以及歐美先進戰(zhàn)斗機對于操縱面的實際使用和分配情況,給出了“確立主控舵面,其它舵面為輔”的操縱面組合分配設(shè)計思路。在具體實施時,首先根據(jù)各個基控制組轉(zhuǎn)矩可達集的大小及其偏轉(zhuǎn)的阻力特性、雷達反射特性確立主控舵面,當主控舵面不能滿足飛行對于可用力矩的需求時,啟用其他輔助操縱面及推力矢量操縱面。隨后的仿真算例驗證了本文提出的方法對于多操縱面分配方案設(shè)計及轉(zhuǎn)矩可達集求解的有效性。

參考文獻：

[1] 楊恩泉, 高金源. 先進戰(zhàn)斗機控制分配方法研究進展[J]. 飛行力學, 2005, 23(3):1-4

Yang Enquan, Gao Jingyuan. Research and Development on Advanced Fighter Control Allcoation Methods[J]. Flight Dynamics, 2005, 23(3):17-19 (in Chinese)

[2] 王美仙, 李明. 先進戰(zhàn)斗機控制分配方法研究綜述[J]. 飛機設(shè)計, 2006(3): 17-19

Wang Meixian, Li Ming. Development of Advanced Fighter Control Allocation Methods[J]. Aircraft Design, 2006(3): 17-19 (in Chinese)

[3] William C Reigelsperger, Siva S Banda. Nonlinear Simulation of a Modified F-16 with Full-Envelope Control Laws. Control Engineering Practice, 1998(6): 309-320

[4] 史靜平, 章衛(wèi)國, 李廣文, 劉小雄. 小生境遺傳算法在廣義逆控制分配法中的應(yīng)用[J]. 系統(tǒng)仿真學報, 2009, 21(20): 6593-6596

Shi Jingping, Zhang Weiguo, Li Guangwen, Liu Xiaoxiong. Application of Niche Genetic Algorithm in Optimization of Generalized Inverse Control Allocation Method[J]. Journal of System Simulation, 2009, 21(20): 6593-6596 (in Chinese)

[5] Bordignon K A. Constrained Control Allocation for Systems with Redundant Control Effectors[D]. Virginia Polytechnic Institute and State University, 1996

[6] 史靜平, 章衛(wèi)國, 李廣文, 劉小雄. 再分配偽逆法分配效率研究[J]. 中國科學:信息科學, 2010, 53(2): 271-277

Shi Jingping, Zhang Weiguo, Li Guangwen, Liu Xiaoxiong. Research on Allocation Efficiency of the Redistributed Pseudo Inverse Algorithm[J]. Science China Information Sciences, 2010, 53(2):271-277 (in Chinese)

[7] Durham W C. Constrained Control Allocation: Three Moment Problem[J]. Journal of Guidance, Control, and Dynamics, 1994,17(2): 330-336

[8] Durham W C. Attainable Moments for the Constrained Control Allocation Problem[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(6): 1371-1373

[9] Durham W C. Computationally Efficient Control Allocation[J]. Journal of Guidance. Control and Dynamics, 2001, 24(3):519-524

[10] Petersen John A M, Bodson Marc. Constrained Quadratic Programming Techniques for Control Allocation[J]. IEEE Transactions on Control Systems Technology. 2006, 14(1):91-98

[11] 楊恩泉, 高金源, 李衛(wèi)琪. 多目標非線性控制分配方法研究[J]. 航空學報, 2008, 29(4):995-1001

Yang Enquan, Gao Jinyuan, Li Weiqi. Research on Multi-Object Nonlinear Control Allocation Method[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(4):995-1001 (in Chinese)

[12] 楊凌宇, 范彥銘, 邵山,等. 基于基排序法的冗余操縱面控制分配與管理[J]. 中國科學:技術(shù)科學, 2010, 40(4):399-406

Yang Linyu, Fan Yanming, Shao Shan, et al. Control Allocation and Management of Redundant Control Effectors Based on Bases Sequenced Method[J]. Science China Technological Sciences, 2010, 40(4): 399-406 (in Chinese)

[13] Addington G A, Myatt J H. Control Surface Deflection Effects on the Innovative Control Effectors Design[R]. AFRL-VA-WP-TR-2000-3027