一種改進的矩陣束模態參數估計方法

譚博, 侯玉, 鄭華, 裴承鳴

(1.西北工業大學 數據處理中心, 陜西 西安 710072; 2.中航工業西安飛機集團有限責任公司, 陜西 西安 710089)

結構模態參數是結構動力學的主要參數之一,具有簡明、直觀、物理概念清晰等優點。通過系統的結構模態參數可以建立相應的數學模型,進而根據載荷下的響應對設計進行必要的調整和修改。在工程應用中,實際觀測到的信號一般是隨機過程,且具有信噪比低、模態密集、有效樣本短等特征,這樣一來,對基于觀測的模態參數估計方法就提出了近乎苛刻的要求。

矩陣束方法是20世紀80年代末、90年代初由Hua和Sarkar提出的一種模態參數估計方法,已經在飛行器、汽車、橋梁以及建筑物的設計中有了廣泛的應用。但是,在實際應用當中發現,該方法的參數估計質量經常會受到諸如樣本長度、信噪比等的影響。為此,本文結合隨機減量技術對矩陣束方法進行了改進,并應用蒙特卡羅方法對改進后方法的數值性能進行了分析研究。

1 改進的矩陣束方法

單模態自由度線性系統運動微分方程為:

(1)

其位移響應x(t)為:

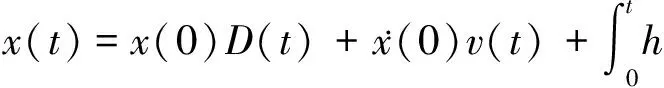
(2)

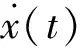
選取適當的A,選取響應中x(ti)=A的點,其中交點對應的時刻為ti(i=1,2,…)。由于是線性系統，對于自ti時刻起的響應x(t-ti)可以看成是由ti時刻的初位移、初速度和隨機激勵引起的強迫響應的三者線性疊加。可以由(3)式表達:

(3)

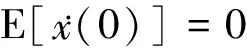
E[X(t)]=E[(x(0)|x(0)=A)]D(t)=AD(t)

(4)

上式表明子響應過程X(t)可以看做一個初位移為A,初速度為零的自由振動響應。對于多模態振動系統,若其系統是線性非時變的,可看做是2個或多個單模態自由度系統的線性疊加。

所得子響應過程X(t)可以表示為如下M個模態的指數函數的線性組合:

(5)

式中:s(t)為系統響應,n(t)為殘留的系統噪聲,t∈[0,T],T為最大觀測時間。對第i個模態,算子si=-αi+jωi可用于表示模態的頻率和阻尼比系數,其中ωi為角頻率,αi為阻尼比系數。

(5)式的離散時間形式為:

(6)

式中：zi=exp(siTs)為系統響應的極點,Ts為采樣周期,k=0,1,2,…N,N為最大采樣點數。

由X(t)可以構造如下的Hankel矩陣:

(7)

式中：L為矩陣束參數,通常取值位于N/4～N/3之間。

對矩陣Y進行奇異值分解,得到:

X=UDVT

(8)

式中：U為(N-L)×(N-L)的正交矩陣;V為(L+1)×(L+1)的正交矩陣;D為(N-L)×(L+1)的對角陣,主對角線上的元素為Y的奇異值。

在已知模態個數M的情況下由D的前M個較大的非零奇異值形成如下新的矩陣D′:

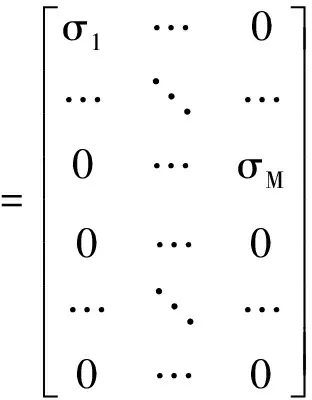
(9)

D′的前M行為一個由σ1…σM構成的M×M維的對角陣,其余行均為0。

(10)

(11)

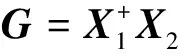
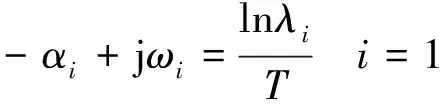
(12)

2 計算機仿真結果及分析

工程中采集得到的信號總是存在噪聲影響,信噪比的大小會直接影響矩陣束方法的計算精度。本節將通過仿真信號對矩陣束方法在噪聲環境下的數值性能進行研究。設置一個雙模態自由度系統,模態參數分別設置為:f1=11 Hz,f2=17 Hz,d1=0.05,d2=0.03。使用矩陣束方法對加噪后的信號進行模態參數估計運算,并對計算結果進行統計,表1顯示的是1 000次計算的最終統計結果。

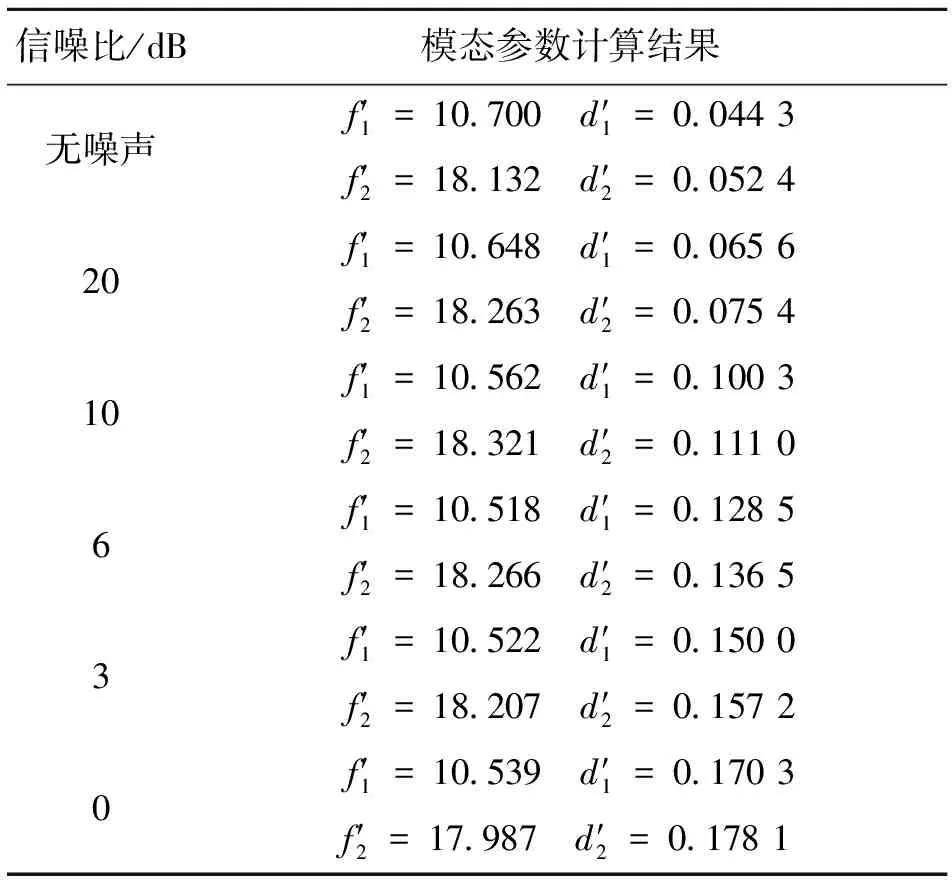
表1 不同信噪比下矩陣束方法的計算結果

由表1可以明顯看出,矩陣束方法估計所得頻率受噪聲影響較小,隨著信噪比下降沒有發生明顯變化,而估計所得阻尼比系數隨著信噪比下降有較大幅度變化,在噪聲能量和加噪前的原始信號能量相等的情況下,估計值的誤差甚至達到了真實值的2～3倍,這會影響矩陣束方法的工程應用。

通過仿真實驗結果可以看出,在其余條件均保持不變,僅改變信噪比的情況下,矩陣束方法所得的阻尼估計結果會產生較大的波動。

為減輕噪聲對矩陣束方法阻尼比估計結果的不良影響,下面將使用引進的矩陣束方法對含有噪聲的信號進行處理。同時加入常用的帶通濾波器降噪方法的計算結果以便于和本文方法進行橫向比較,其統計結果分別如表2和表3所示。

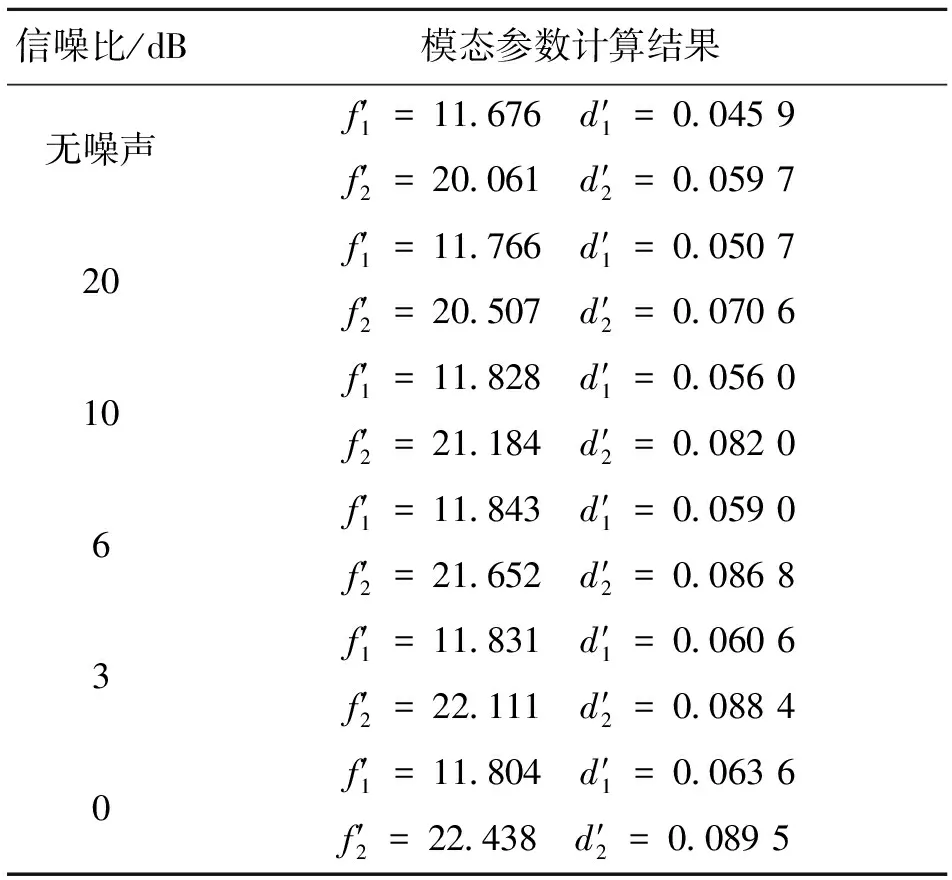
表2 通過帶通濾波器處理后的計算結果

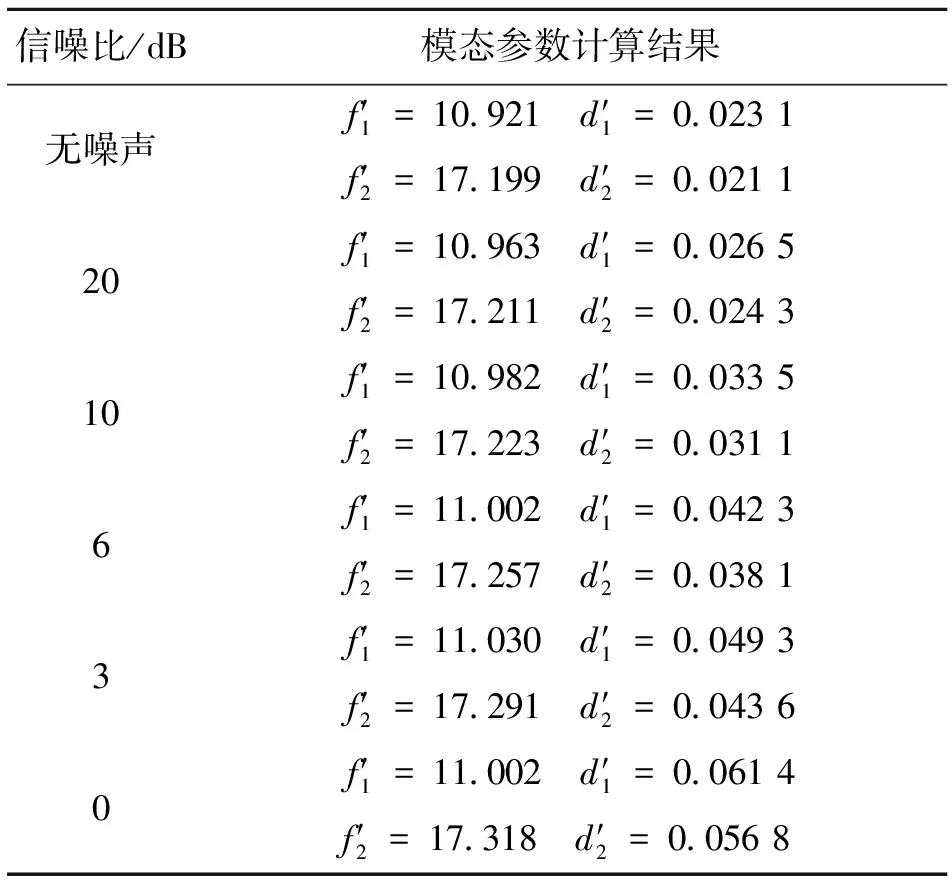
表3 改進的矩陣束方法的計算結果

由表1和表2的對比可以看出,通過帶通濾波器以后,信號中噪聲的能量受到抑制,盡管計算所得的阻尼比隨著噪聲能量的增大依然有所增加,但是增加幅度明顯比未經處理的信號得到的結果要小,在噪聲能量和加噪前原始信號能量相等的情況下,計算結果的誤差約為真實值的一半,計算精度已經有所改善。但可以注意到,盡管阻尼比的計算精度有了明顯提高,但是計算所得的頻率同真值相比的差距反而增大,因此僅通過帶通濾波器不能很好地改善矩陣束方法的數值性能。

下面將使用本文方法對數據進行處理,并對計算結果進行統計。

由表3可以看出,本文方法的計算精度與傳統的矩陣束方法相比有大幅的提高,其計算頻率的最大誤差不到2%;當原始信號能量與噪聲能量相等的時候,其計算阻尼的誤差約為20%,與帶通濾波器處理后的計算結果相比,精度有進一步的提高。

為了進一步研究3種方法的數值性能,下面將以阻尼比為0 dB,即噪聲和原始信號能量相等的情況為例,研究3種方法在此信噪比下1 000次計算結果的分布情況。

圖1和圖2展示的為1 000次計算結果的統計分布,真實頻率為11 Hz,真實阻尼比系數為0.05。圖中,梗狀圖為計算結果(阻尼或頻率)分布,實線為高斯擬合曲線,橫軸中點均為真實值;由圖a)至圖c)依次對應矩陣方法、帶有濾波器的矩陣束方法以及本文方法的計算結果。

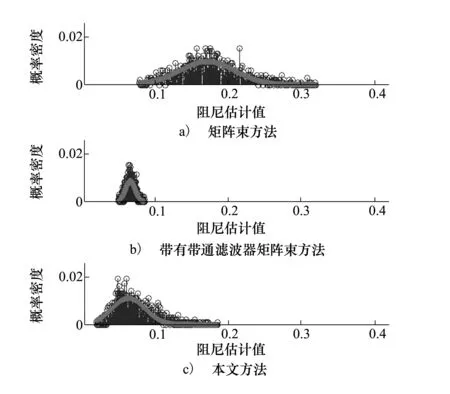
圖1 計算阻尼分布

由圖1中3種方法結果的對比可以看出,矩陣束法的計算結果整體偏離真實值較遠,而且分布較散,這表明每次的計算值會在一個較大的范圍內波動,不利于通過計算確定模態的參數。而引入通濾波器后信號的計算結果分布集中,且計算的阻尼比系數與真值的差明顯縮小,矩陣束方法的數值性能得到了改善。本文方法的結算結果盡管不如第二種方法所得結果理想,但是其也較為集中分布在真實值附近,相比傳統的矩陣束方法,其具有更好的數值性能。

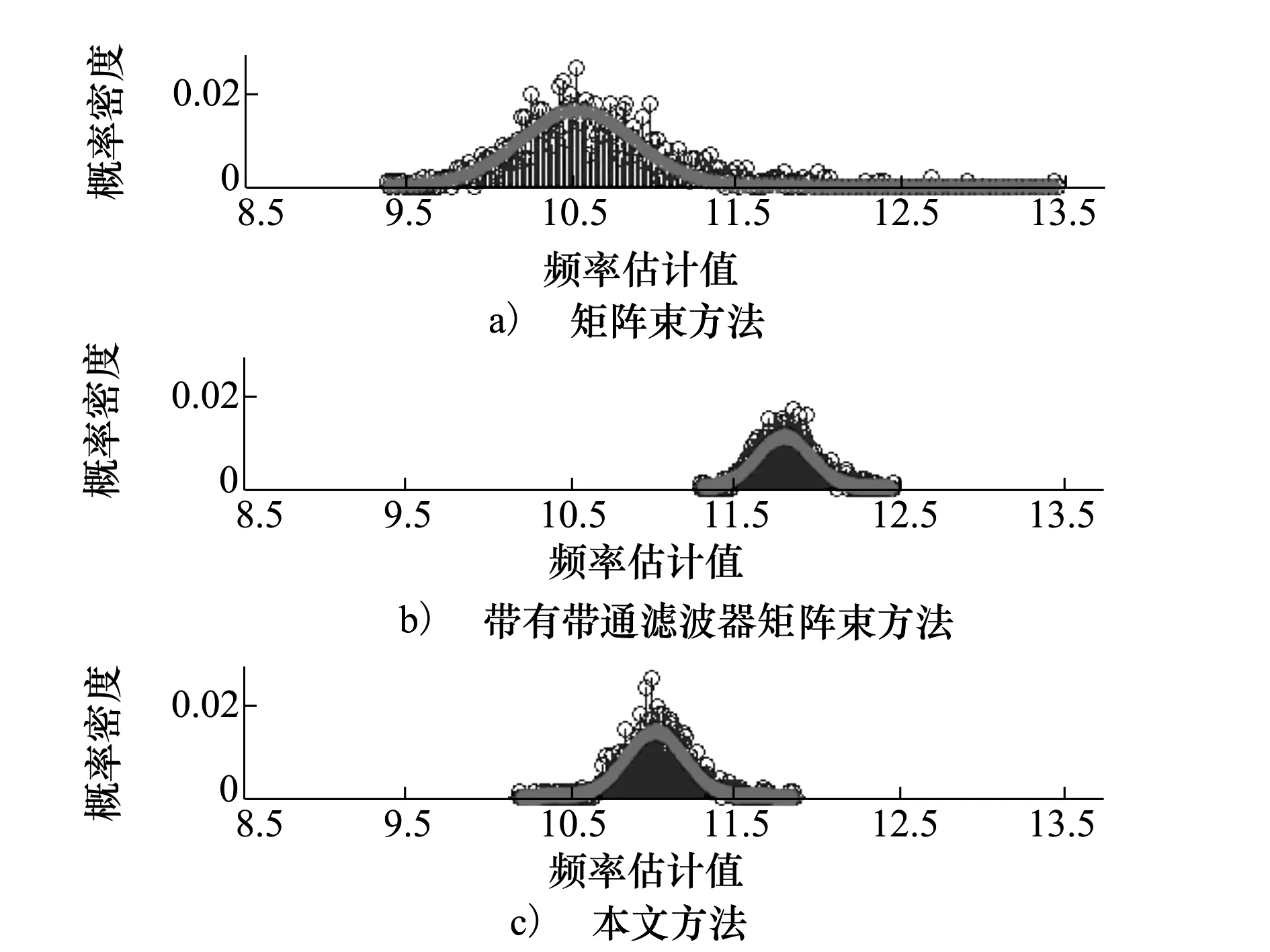
圖2 計算頻率分布

由圖2可以看出,在頻率的估計方面。矩陣束方法和引入濾波器的矩陣束方法的計算結果均與真實值有一定的差異,相比之下,帶有濾波器矩陣束方法的結果分布更加集中,略微地改善了矩陣束方法的估計頻率結果精度,但是仍然和真實值相差較大,而本文方法所得結果更為理想,其頻率的精度較前兩種方法的結果有明顯提高。

綜上所述,本文方法可以有效的提升矩陣束方法的參數估計結果的精度,與帶通濾波器這種傳統的降噪方法相比也具有一定的優勢。

3 結 論

借助隨機減量技術,本文提出了一種改進的矩陣束方法,經計算機仿真及蒙特卡羅統計分析,驗證了本文方法在模態參數估計方面的合理性和有效性。通過提高矩陣束方法的計算結果精度,還可進一步用于解決模態參數估計中的一些其他常見問題,如密集模態等。可以預見,該方法對于包括結構顫振在內的航空航天領域有著重要的工程實用意義。

參考文獻：

[1] Thomas A J, Chard J, John E, Davies A, Francis M. Defining a Bearing Replacement Strategy Using Monte Carlo Methods[J]. International Journal of Quality & Reliability Management, 2011, 28(2): 155-167

[2] Daniel Potts, Manfred Tasche. Parameter Estimation for Nonincreasing Exponential Sums by Prony-like Methods[C]∥17thConference of the international Linear Algebra Society,Braunschweig,Germany, 2013: 1024-1039

[3] Chiu Jen Ku. Random Decrement Based Method for Modal Parameter Identification of a Dynamic System Using Acceleration Responses[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95: 389-410

[4] 朱瑞可,李興源,王渝紅,趙睿,胡楠,李寬. 基于矩陣束算法的諧波和間諧波參數估計[J]. 華東電力, 2012, 40(3): 388-391

Zhu Ruike, Li Xingyuan, Wang Yuhong, Zhao Rui, Hu Nan, Li Kuan. Parameter Identification of Harmonics and Interharmonics Based on Matrix Pencil Algorithm[J]. East China Electric Power, 2012, 40(3): 388-391 (in Chinese)

[5] 莊銘杰. 蒙特卡洛仿真在移動通信中的應用研究[J]. 計算機仿真, 2004, 21(11): 116-120

Zhuang Mingjie. Application of Monte-Carlo Simulation in Mobile Communications[J]. Computer Simulation, 2004, 21(11): 116-120 (in Chinese)

[6] 張敏,黃俐,李文雄,鐘學賦. 大型結構模態參數識別研究[J]. 建筑科學與工程學報, 2013, 30(2): 49-54

Zhang Min, Huang Li, Li Wenxiong, Zhong Xuefu. Research on Modal Parameter Identification on Large-Scale Structure[J]. Journal of Architecture and Civil Engineering, 2013, 30(2): 49-54 (in Chinese)

[7] 徐利,鄒傳云,陳民,何毅. 基于矩陣束算法的極點提取分析[J]. 通信技術, 2012, 45(6): 58-60

Xu Li, Zou Chuanyun, Chen Min, He Yi. Analysis on Pole Extraction Based on Matrix Pencil Algorithm[J]. Communications Technology, 2012, 45(6): 58-60 (in Chinese)