一種改進的模型驅動PID的應用研究

(華北電力大學 自動化系，河北 保定 071000)

一種改進的模型驅動PID的應用研究

喬靜兵，何同祥

(華北電力大學 自動化系，河北 保定 071000)

對模型驅動PID(簡稱MD-PID)控制算法進行介紹，提出了一種改進的模型驅動PID (簡稱A-MD-PID) 控制算法，并應用于二階慣性加純遲延對象，用MATLAB進行仿真研究。結果表明，本文采用的改進模型驅動PID，能有效地克服被控對象的慣性和遲延，提高系統的控制品質。

模型驅動PID；改進算法；仿真研究

0 引言

PID控制[1]是應用比例、積分、微分環節對偏差進行運算的一種綜合控制。PID控制器[2]具有原理簡單、使用方便、魯棒性強、其控制品質對過程變化靈敏度低、控制器參數整定比較容易、無靜差調節等特點，一直是工業過程控制領域的主導控制器。但是在熱工控制過程中，大型單元機組大多都是大慣性、大遲延的特性，應用簡單的PID控制器控制很難達到理想的控制效果，而且參數整定也比較困難。

隨著計算機的飛速發展和控制理論的廣泛應用，已有的PID控制算法已經滿足不了當今社會的發展，人們開始對先進PID控制算法地研究。基于內模控制[3]的各種控制算法由于設計原理簡單，應用范圍廣，控制性能優越，而引起過程控制界的關注。模型驅動PID控制是2002年由Shibaura、Tokyo等人提出來的一種基于內模控制的較新型控制算法[4]。它將等效被控對象模型近似為一階慣性加純遲延。但在熱工過程控制系統中，這種一階近似模型與實際被控對象的動態特性差距較大，不易取得好的控制效果，所以沒有得到普遍應用。本文在原有模型驅動PID算法的基礎上，將等效被控對象模型近似為二階慣性加純遲延，推導出新的控制算法公式。文中通過MATLAB仿真對A-MDPID和原MD-PID進行比較，結果表明，A-MD-PID獲得了良好的控制品質。

1 模型驅動PID控制系統及改進

1.1模型驅動PID控制基本算法

模型驅動PID控制[4]，通過增加一個PD反饋補償環節，將等效被控對象近似為一階慣性加純遲延，然后以此等效被控對象作為參考模型，應用內模控制的設計方法來設計控制器。如圖1所示。

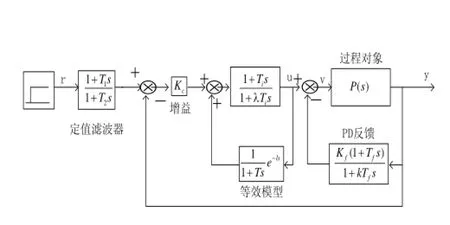
圖1 MD-PID控制系統原理圖Fig.1 MD - The principle diagram of the PID control system

根據圖1，MD-PID控制系統基本算法可用下式來描述：

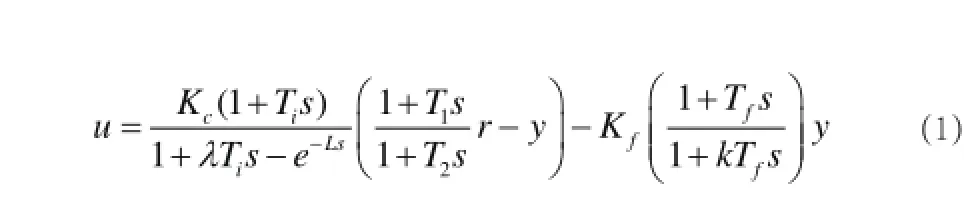
具體算法[4]如下：

通過麥克勞林展開公式可以將被控對象傳遞函數用下式展開：

PD反饋補償器為：

由式(2)、(3)得:

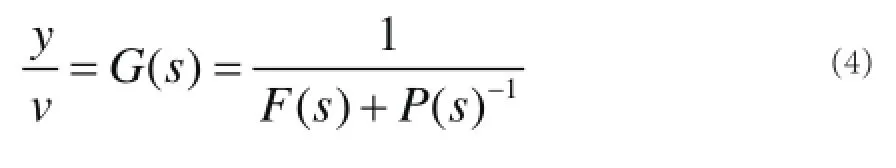
F(s)通過下式設計：

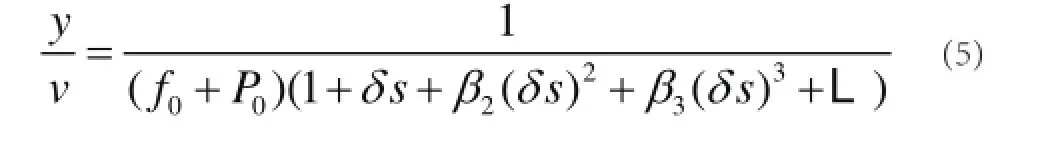
等效被控對象模型為：

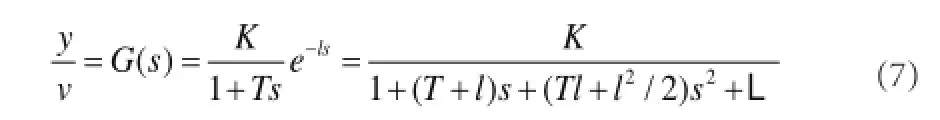
由式(5)～(7)得等效被控對象模型參數：

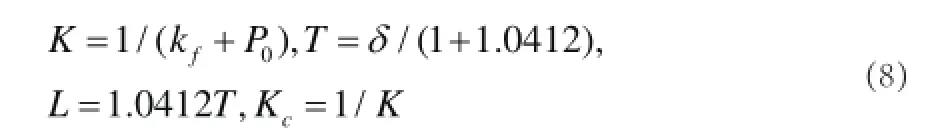
1.2模型驅動PID的改進

對模型驅動PID做如下兩點改進：

1）將等效被控對象模型由一階慣性加純遲延改進為二階慣性加純遲延。

2）對計算過程進行改進，推導出新的計算公式：原算法是由被控對象模型求取PD反饋參數，然后再求等效被控對象模型；改進算法為根據對等效被控對象模型的期望，來指定等效被控對象模型，然后再計算PD反饋中的參數。如圖2所示。

根據圖2，A-MD-PID控制系統可用下式來描述：

通過麥克勞林展開公式將被控對象傳遞函數展開為：

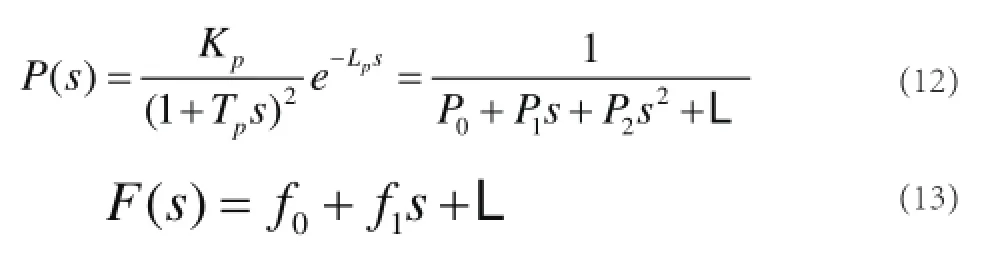
由式(12)、(13)得：

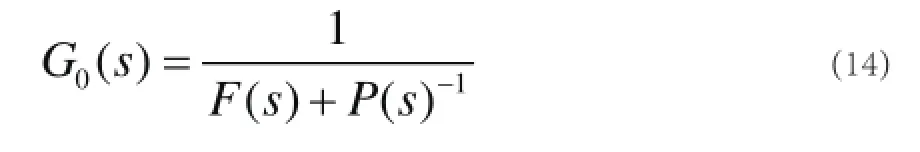
期望的等效被控對象模型為：

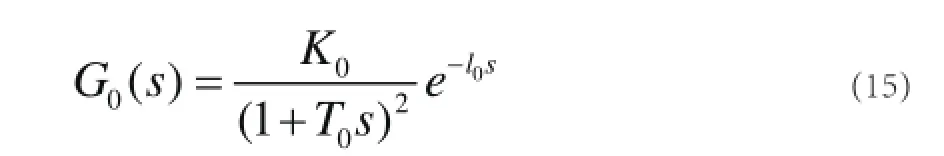
通過麥克勞林展開公式將式(15)展開得：

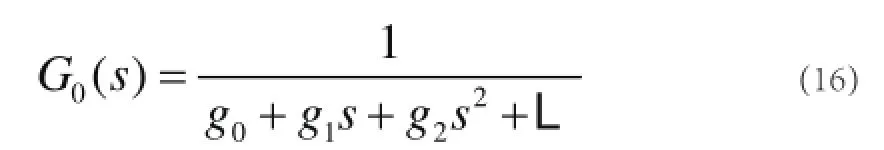
指定T0，l0，由式(17)得K0

最后得出PD反饋補償器F(s)中參數：

圖2中定值濾波器是一個超前滯后環節，用于對設定值做處理，主要在設定值變化時對設定值做調理。

2 MATLAB仿真

為了檢驗A-MD-PID算法的控制效果，本文采用MATLAB中的SIMULINK工具，對A-MD-PID和原MD-PID控制算法進行仿真研究。

選取被控對象[5]傳遞函數為：

等效被控對象模型為：

PD反饋補償器為（k=0.1）：

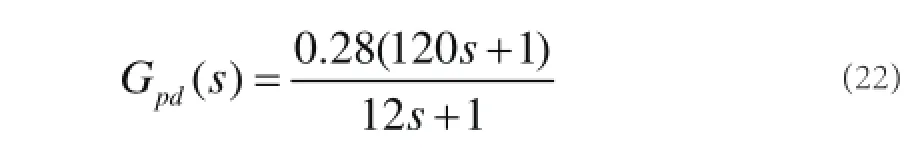
采用A-MD-PID控制、原MD-PID控制和PID控制，在定值階躍擾動下的系統輸出響應曲線如圖3所示。仿真結果表明，A-MD-PID控制效果較好。

圖3 模型匹配時階躍響應曲線圖Fig.3 Model matching step response curve

大型單元機組在工業現場總是存在各種各樣的噪聲和擾動，而且用模型代替實際被控對象總會有誤差，因而控制系統需要有一定的魯棒性。憑經驗所知，一般在工程中，當K增大、T減小、l增大時模型失配的情況是最難控制的。假設被控對象的K、l各增加10%，T減小5%，即K=3.96，T=142.5，l=71.5s。在定值階躍擾動下的系統輸出響應曲線如圖4所示。仿真結果表明，A-MD-PID算法具有良好的魯棒性。

3 結束語

圖4 模型失配時階躍響應曲線圖Fig.4 Step response curves of model mismatch

本文在由Shibaura、Tokyo等人提出來的模型驅動PID控制的基礎上，提出了改進模型驅動PID控制算法。通過MATLAB仿真驗證了改進模型驅動PID控制的優越性。相比模型驅動PID基本算法，改進模型驅動PID不僅能有效地克服被控對象的大慣性和大遲延，抑制了超調量，而且兼顧了系統的快速性，從而提高了系統的控制品質。文中提出的改進模型驅動PID控制算法，經過簡單地轉換、組合，可以采用DCS常規功能塊組態實現，也可以通過DCS用戶自定義模塊編程實現，是一種有推廣價值的新型控制算法。

[1]楊智,朱海峰,黃以華． PID控制器設計與參數整定綜述 [J]．化工自動化及儀表, 2005 , 32( 5 )： 1- 7．

[2]韓璞,智能控制理論及應用[M]．北京：中國電力出版社,2012：141-144．

[3]靳其兵,黃文兵． 兩種 IMC-PID整定方法的比較[J]化工自動化及儀表, 2010 , 37( 4)： 10-12．

[4]Toshiba-Cho, Fuchu-shi, Toky． A Model-Driven PID Control System and its Case Studies [J]．2002：18-20．

[5]張艷娟． 超臨界鍋爐再熱汽溫控制系統研究[D]． 保定：華北電力大學, 2008．

The Application of an Improved Model Driven PID

Qiao Jingbing, He Tongxiang
（Automation Department, North China Electric Power University, Baoding 071000,China）

A brief introduction to model driven PID (MD-PID) control algorithm. An improved model driven PID (A-MDPID) control algorithm is put forward, and applied to the control system with two order lag and delay process, and studied by MATLAB. The simulation results show that A-MD-PID can effectively overcome the lag and delay of controlled object, so improve the performance of control system.

model-driven PID; algorithm improvement; simulation research

TP273+.3

A

Doi：10.3969/j.issn.1671-1041.2014.03.025

2014-03-20

喬靜兵，女，碩士研究生，從事智能控制、協調控制系統優化等研究。