三相PWM 整流器的魯棒反演控制器設計

吳桂良，田永貴，李小明，程穎菲

(1．西南交通大學 電氣工程學院，四川 成都610031;2．西安鐵路職業技術學院，陜西 西安710014)

0 引言

以脈寬調制(PWM)控制為基礎的各類變流裝置在國民經濟各個領域中已取得廣泛應用。其在高壓直流輸電、有源電力濾波器、超導儲能、交流傳動等領域的研究應用一直是學術界關注的熱點［1～6］。對其合理建模與深入研究控制策略具有重要意義。

反演法又稱后退法、回退法，因其獨特的構造性設計過程和對非匹配不確定性的處理能力，在控制系統設計中得到了成功應用［7］。反演控制的基本思想是將復雜的非線性系統分解成不超過系統階數的子系統，然后為每個子系統設計部分Lyapunov 函數和空間虛擬控制量，一直后退到整個系統。反演法適用于可以狀態線性化或具有嚴格參數反饋的不確定非線性系統。

對實際對象的數學建模不可避免帶有未建模態、近似參數等不確定因素。不確定性的存在使實際對象與所用數學模型之前存在差別，僅根據標稱系統設計控制器，會使大量工程控制問題無法獲得滿意結果，甚至嚴重影響系統性能［8］。魯棒控制理論就是針對系統的不確定性的存在而提出的，它的優點在于抑制干擾和補償未建模動態。

本文考慮到PWM 整流器在實際運行中存在的參數不精確的情況，建立包含不確定性的數學模型。采用反演設計法設計該系統的控制器，同時考慮到不確定性對系統性能的影響，引入魯棒控制項對該影響進行補償，增強系統的魯棒性。應用Lyapunov 穩定性定理證明該系統為漸進穩定。在Matlab 中搭建仿真模型，驗證所設計控制器的有效性。

1 三相VSR 暫態數學建模

三相VSR 拓撲結構如圖1 所示。

圖1 三相PWM 整流器拓撲結構

根據電路關系列寫電流微分方程，并經Park變換后可得到下式［9］:

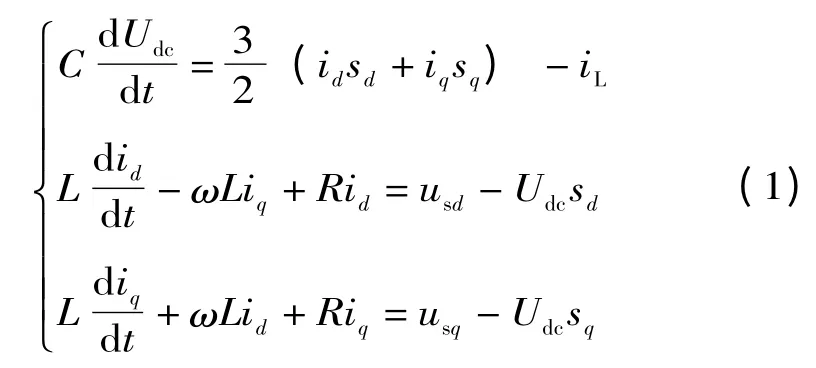
式中:id，iq為交流側電流的d，q 分量;sd，sq為單極性二值邏輯開關函數;usd，usq為電網電壓的d，q 分量;RL為負載等效阻抗，其余符號含義見圖1。

交流側與直流側的有功功率分別為:

當忽略三相橋的自身損耗時，交流側與直流側的有功功率相等，聯立式(2)、(3)并化簡，可得:

定義新變量u，并令

VSR 交流側輸出電壓的d，q 分量vd，vq為

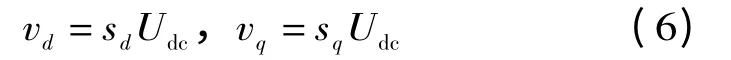
定義新變量ud，uq，并令

將式(5)、(7)代入(1)、(4)，可得三相VSR 在dq 坐標系中的數學模型

對于新變量u，ud，uq，式(8)為一組線型微分方程。

在實際系統中，受VSR 運行狀態改變等因素的影響，R，L，RL這些參數通常不能精確測定。考慮它們的偏差為ΔR，ΔL，ΔRL，從而將系統模型(8)改寫為(9)式。

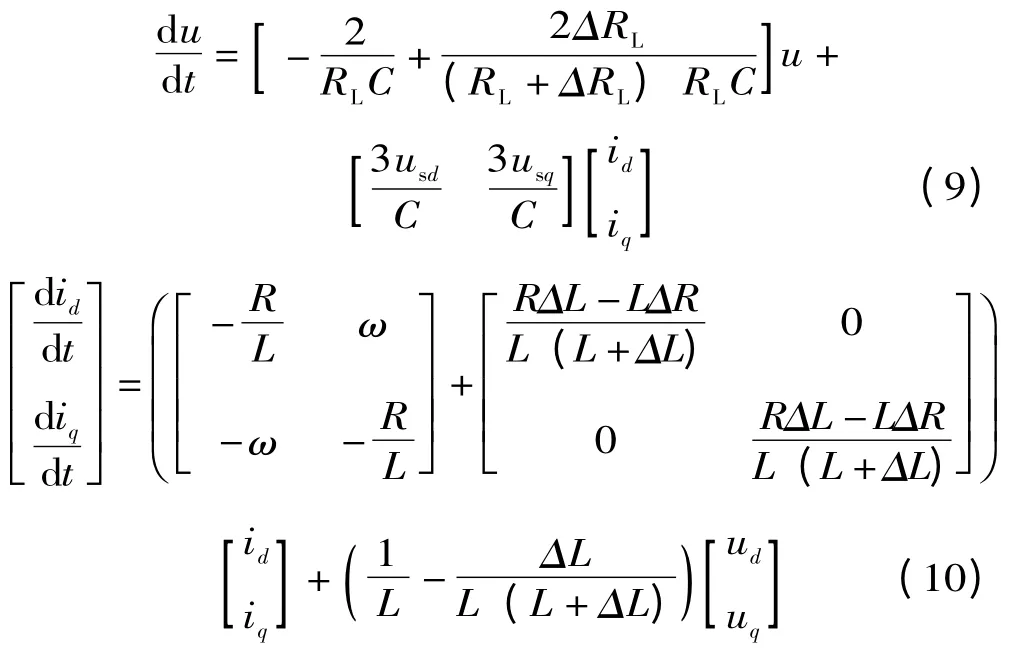
定義x1=u，x2=［idiq］T，μ=［uduq］T，則可得到VSR 的不確定模型:

2 控制器設計與穩定性分析

為消除不確定性對系統的影響，保證在所有信號有界的前提下，系統狀態指數收斂至系統遠點的某一任意小的領域，對該系統設計一個魯棒反演控制率。按照反演控制的設計方法，定義虛擬狀態和虛擬控制，并在虛擬控制和實際控制中引入一個魯棒項，以克服不確定的影響。

引入新的誤差狀態向量z1，z2［10］，

式中:x1d，x2d為系統期望的狀態軌跡。對z1，z2求導可得狀態誤差的動態方程為

以下分兩步進行控制器設計。

第一步:將系統式(14)重寫為以下形式

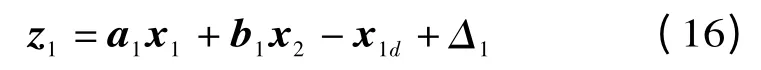
式中:Δ1為因參數不精確的影響而引入的不確定項，將通過引入一類魯棒函數來補償這種不確定性的影響。

假設1 存在一個未知的正數ρ1，使得

其中，δ1(x1，x2)為已知的非負光滑函數。

將x2看做子系統(16)的虛擬控制量，并在x2d中引入魯棒控制項v1［11］來消除不確定性的影響，選取期望的虛擬控制量為

其中，k ＞0，ε1，a ＞0 為設計參數，為b1的廣義逆。

選取Lyaponuv 函數

沿(16)式的方向對其求導可得:

第二步:重寫(15)為

假設2 存在一個未知的正數ρ2，使得

其中，δ2(x1，x2)為已知的非負光滑函數。

同理，取

其中，K2=diag(k21，k22)，k21，k22＞0，ε1，a ＞0 為設計參數。

式(24)即為控制器的輸出方程。

選取Lyaponuv 函數

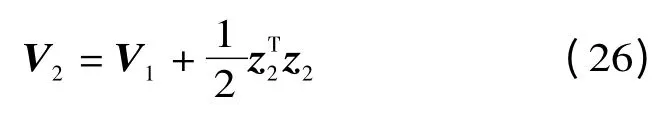
對(26)式求導可得:

由Lyaponov 穩定性分析可知該系統為漸進穩定［13］。由此可設計魯棒反演控制器如圖2 所示。

圖2 魯棒反演控制器結構

3 仿真

為驗證控制器性能，在Matlab/Simulink 中搭建如圖3 所示的仿真模型。選取系統參數為RL=50 Ω，R=0．1 Ω，L=0．01 H，C=3 mF，交流側電壓usa，b，c=240 V，直流側電壓Udc=500 V，并假設參數誤差＜30%。選取設計參數k1=45，k2=diag［93，93］，ε1=0．3，ε2=0．5，ρ1=3，ρ2=5，a=0．01。

圖3 三相整流器仿真模型

在0．3 s 時，系統交流側發生A 相單相接地短路，接地阻抗為1 mΩ，0．35 s 時故障切除，系統恢復正常運行。仿真結果如圖4 所示。

圖4 仿真波形圖

由圖4 可見，0．3 s 時系統發生短路故障，各變量發生小幅震蕩，在0．35 s 時短路故障解除，各狀態量可在短時間內恢復至正常運行狀態，表明控制器可有效跟蹤基準值，跟蹤速度較快，跟蹤誤差較小。仿真結果表明，當選取合適的設計參數時，系統可正常運行并具有良好的動態性能。證明控制器具備良好的動態品質與跟蹤性能。

4 結論

本文采用反演的控制方法對含有不精確參數的PWM 整流器設計非線性控制器，并在控制項中引入魯棒控制項以補償系統不確定性的影響。在Matlab/Simulink 平臺下搭建仿真模型對所設計控制器性能進行驗證。仿真結果表明，在正確選擇設計參數下該系統具備良好的動態性能與跟蹤性能。

［1］李正熙，王久和，李華德．電壓型PWM 整流器非線性控制策略綜述［J］．電氣傳動，2006，36(1):9-13，27．

［2］馮陽，王奔，王亞芳，等．有源濾波技術在串級調速中的應用［J］．電力科學與工程，2013，29(12):23-30．

［3］Sharma S，Singh B．An enhanced phase locked loop technique for voltage and frequency control of stand-alone wind energy conversion system［C］．New Delhi:2010 India International conference on Power Electronics(IICPE)，2011:1-6．

［4］燕躍豪，鮑薇，李光輝，等．基于混合儲能的可調度型分布式電源控制策略［J］．華北電力大學學報(自然科學版)，2014，41(2):28-35．

［5］郭文勇，趙彩宏，張志豐，等．電壓型超導儲能系統的統一直接功率控制方法［J］．電網技術，2007，31(9):58-63．

［6］Marcos C，Sanchez-pena J M，Towes J C，et al．Note:Phase-locked loop with a voltage controlled oscillator based on a liquid crystal cell as variable capacitance［J］．Review of Scientific Instruments，2011，82(12):126101-126103．

［7］Kokotovic P．Constructive nonlinear control:Progress in the 90's［C］．Beijing，China:Proceedings of IFAC 14nd World Congress，1999，1:49-77．

［8］喬繼紅．反演控制方法與實現［M］．北京:機械工業出版社，2012．

［9］張興，張崇巍．PWM 整流器及其控制［M］．北京:機械工業出版社，2013．

［10］胡云安，晉玉強，李海燕．非線性系統魯棒自適應反演控制［M］．北京:電子工業出版社，2010．

［11］Yeong-Jeu，S．，L．Chang-Hua and H．Jer-Guang，Global exponential stabilization for a class of uncertain nonlinear systems with control constraint．Automatic Control，IEEE Transactions on，1998．43(5):674-677．

［12］伊西多．非線性控制系統(第三版)［M］．王奔，莊圣賢．北京:電子工業出版社，2012．

［13］過希文，王群京，李國麗，等．永磁球形電機的自適應反演滑模控制［J］．南京航空航天大學學報，2014，46(1):59-64．