非對稱結構振型向量的海森陣算法
張 淼
(長春工程學院理學院,吉林長春 130012)
0 引 言
目前在最優化領域中,多元函數的海森陣及多元函數的二階泰勒展開式已經得到廣泛應用,但關于多元向量值函數的海森陣問題的討論,一直很少有文獻提及,實際上海森陣問題構成需要計算向量值函數的二階導數。自1965年發展至今,有關對稱系統振型向量一階導數的計算無論從算法到應用都已相當成熟[1-2],相關的一階泰勒展開式也隨之發展應用。但非對稱系統的振型向量二階導數問題一直沒有很好的解決方案。導數問題在工程中也稱為靈敏度問題,文獻[3]提出了針對非保守系統的靈敏度分析方法,文獻[4]綜述了計算各種振系模態靈敏度的統一算法,文中在此基礎上,首先給出了多元向量值函數的海森陣定義,然后提出了非對稱系統振型向量的海森陣算法,并形成了非對稱系統正則固有振型在設計參數發生擾動后的二階泰勒近似算法,為工程應用提供可靠且高效的算法基礎。
1 多元函數的海森陣
對于多元函數f(x),其中,x=(x1x2…xn)T,f(x)的一階導數稱為它的梯度
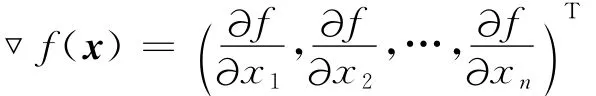
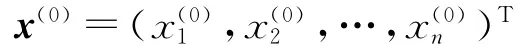

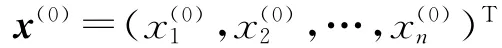
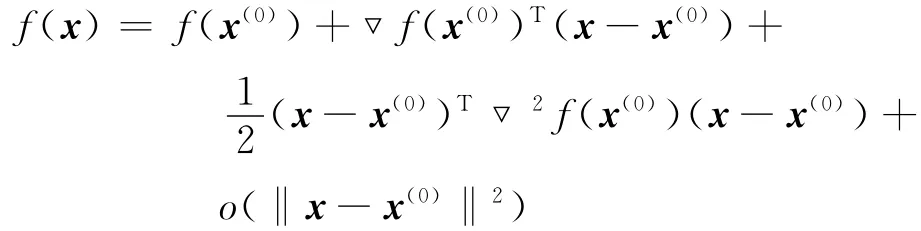
式中:o(‖x-x(0)‖2)——高階無窮小。
仿此,下面給出多元向量值函數的海森陣概念及算法。
2 多元向量值函數的海森陣
若u=(u1(b),u2(b),…,uN(b))T每一維分量均為向量b=(b1,b2,…,bq)T的函數,因此,u=(u1(b),u2(b),…,uN(b))T是多元向量值函數,下面考慮它的二階導數及海森陣算法。
定義1 設多元向量值函數u=(u1(b),u2(b),…,uN(b))T的二階偏導數為:
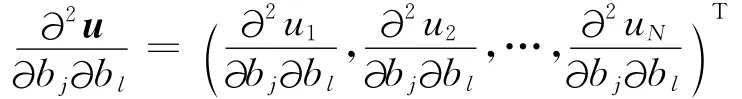
則u=(u1(b),u2(b),…,uN(b))T的海森陣為:
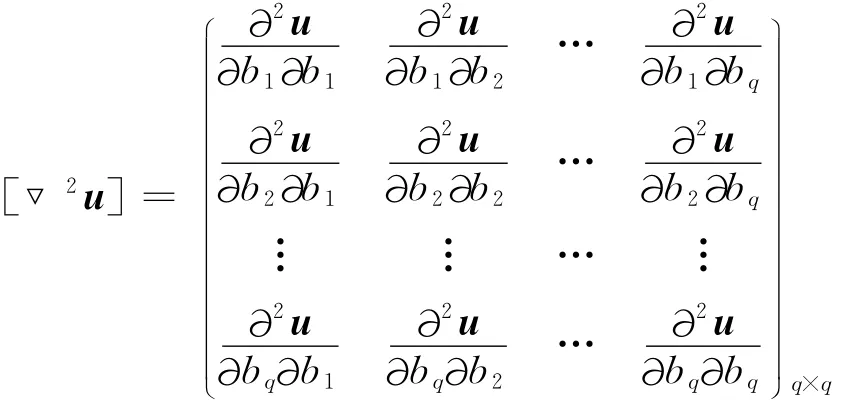
若記

那么海森陣還可改寫為

事實上,多元向量值函數的海森陣只是一個矩陣形式而已,而并不能構成通常意義上的矩陣,因它的每個元素仍是向量,但它可方便用于向量值函數的二階泰勒展開,因此仍可沿用海森陣的名稱。
3 振型向量的海森陣算法及應用
對N自由度的線性離散振動系統的運動方程為:
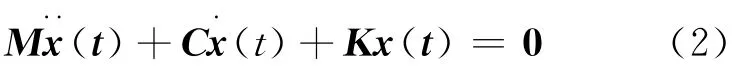
式中:M——對稱系統的質量矩陣,M∈RN×N;
C——對稱系統的阻尼矩陣,C∈RN×N;
K——對稱系統的剛度矩陣,K∈RN×N。
結構有限元分析時,作拉普拉斯變換x(t)=u ewt=u eiωt(w=iω)代入式(2)可得(w2Mu+w Cu+Ku)ewt=0。令C=0,則無阻尼固有頻率(i=1,2,…,N,w2=-ω2)與振型向量為ui(i=1,2,…,N),滿足無阻尼特征方程
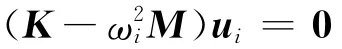
為表達方便,記λi=-(i=1,2,…,N),上式可寫成
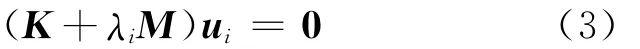
實際上,方程(3)是關于矩陣M和K的廣義特征問題。
研究在設計參數變化時所引起的振型的變化具有廣泛的應用。由于在設計參數發生微小變化時,結構動力特性和動力響應可能會引起很大的變化,在工程中用導數來反映這種變化的程度,有時也稱為靈敏度分析。因此,這一領域的研究在結構動力分析、識別、修改、模態分區及振動控制和優化設計等工程問題中扮演了重要的角色。例如現實工況中設計參數不得不面對損傷,探測及銹蝕等變化,所以人們若不正視在特定環境下的這種變化所引起的嚴重反映,就可能直接影響著結構系統的穩定性[5]。另一方面,由于泰勒展開式在設計參數發生擾動后結構參數隨之發生擾動的幅度的計算中具有良好的應用性,因此,計算結構參數及模態參數的各階導數更加成為一個關鍵環節,但目前靈敏度計算所能達到的應用水平卻很低,許多有限元程序分析軟件中關于導數的使用最多的表達式仍然是差分格式,Ansys中的靈敏度分析實際上是將變量變動1%,然后重新計算變動后的函數值,再用一階和二階差分來作為近似導數,這需要多次重復地計算,因此,文中的研究具有較好的應用價值。
對于N自由度的線性離散振動系統(2),若其在設計、修正和動力分析過程中可以被設計參數向量b=(b1,b2,…,bq)T所描繪,系統的性質矩陣乃至振型向量均可看成是設計向量的函數,相應地特征方程(3)應為(b)u(b)+λ(b)M(b)u(b)=0,為了討論方便,以下仍記為如式(3)的形式。考慮系統的初始狀態,即設計參數取值為b(0)=時,若取得設計參數的微小擾動Δb=(Δb1,Δb2,…,Δbq)T時,那么振型會產生多大的擾動呢?與有關多元函數的泰勒展開方法類似,工程中也考慮在設計參數的初始位置處對振型作二階泰勒近似
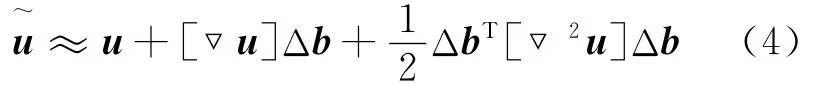
首先規范化每個振型,規范化后的振型向量在應用中常稱為無阻尼正則固有振型。設每個正則化系數為ai,即
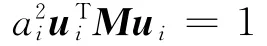
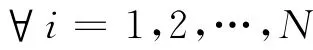
記aiui=φi,則Φ=[φ1,φ2,…,φN]為無阻尼正則固有振型矩陣,對單頻對稱系統而言,不同頻率所對應的振型關于矩陣M和K是加權正交的,即有
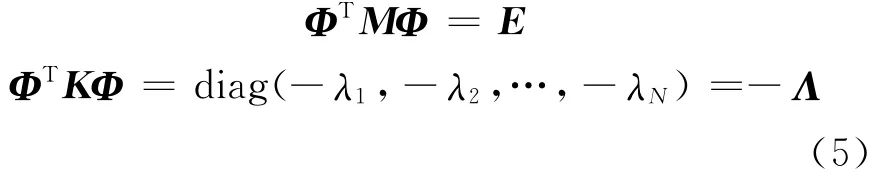
但如果系統為非對稱系統,無法證明不同頻率所對應的實模態是關于質量和剛度陣加權正交[6],因此,需引入新的向量來實現類似式(5)的規范正交化。先將特征方程轉化為一般特征問題
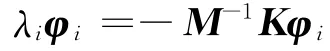
令
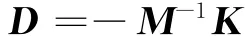
則上式寫成

φi(下文中也稱為D的右特征向量)并不能對角化D,因為D一般為非對稱矩陣,因此引入左特征向量。
定義2 對向量Ψk∈RN,如果有
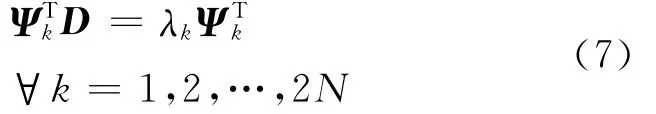
則稱Ψk∈RN為矩陣D的左特征向量。
對式(7)右乘φi,對式(6)左乘,然后相減,顯然對于λk≠λi,有

并由式(8)可知

上式說明,對不同的特征值,矩陣D的左、右特征向量不僅滿足正交性,而且滿足關于D的加權正交性。適當規范化這些左右特征向量,令

則根據式(7)有

且為了后文需要補充一個規范化要求:令Ψi,φi第ni個分量元素是相等的[3],即
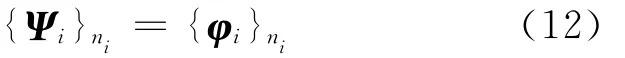
{·}i代表向量的第i個分量,其次ni的選取是依據下列原則
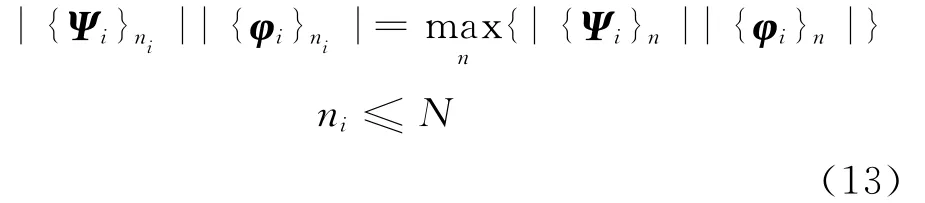
記Ψ=[Ψ1,Ψ2,…,ΨN]為左特征向量矩陣,那么由式(8)~式(11)構成下面規范正交化條件

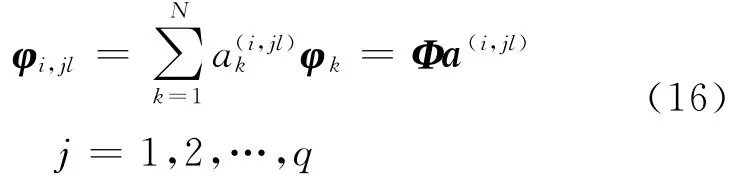

然后是對第l個設計參數bl求二階導數得
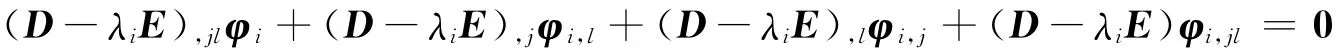
整理得
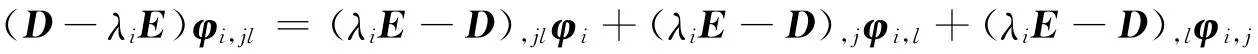
將式(11)代入上式,并左乘ΨT得
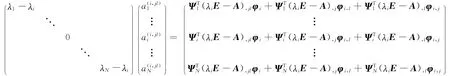
可見除了方程組中的第i個方程外,均可解得
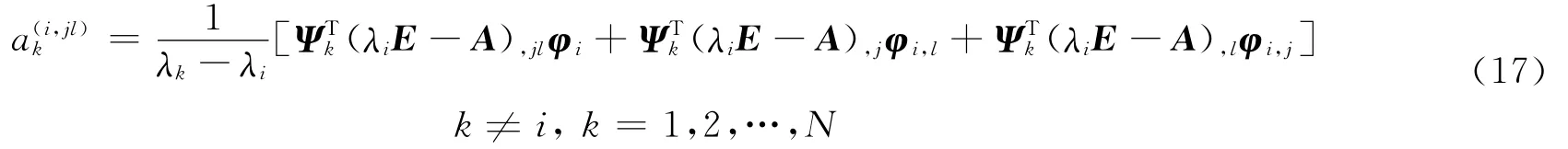
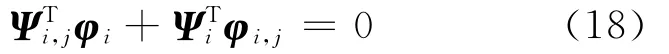
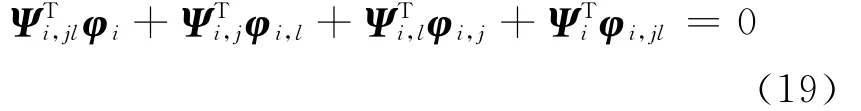
然后是關于第l個設計參數bl求導得做與式(16)類似的假定,將Ψi,jl在其完備的左特征空間中展開為
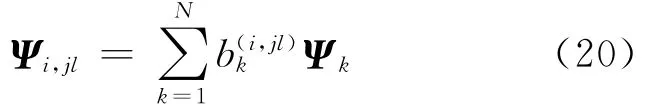
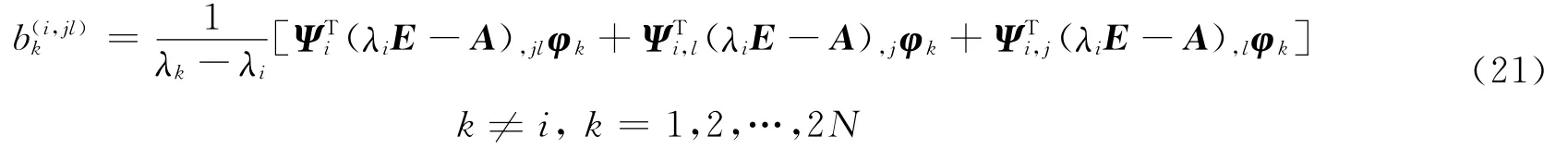
將式(16)與式(20)代入式(19),并使用正交性(見式(8))得

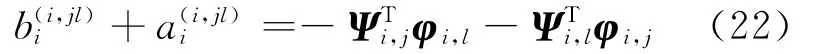
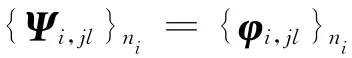
把式(16)與式(20)代入上式得
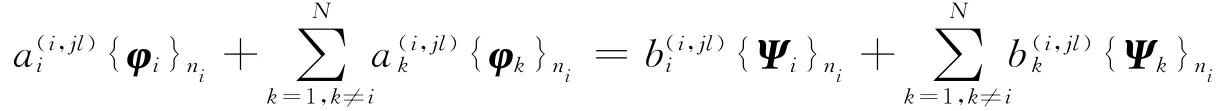
依據式(12),即
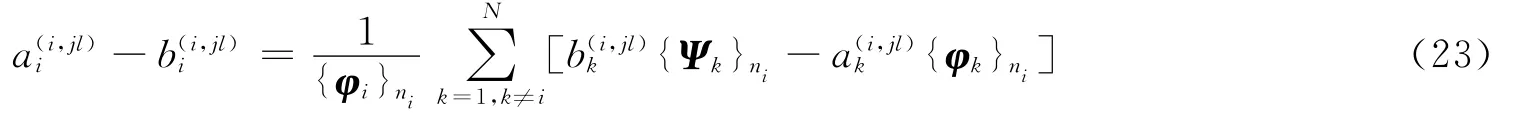
由式(22)和式(23)兩個方程可解得
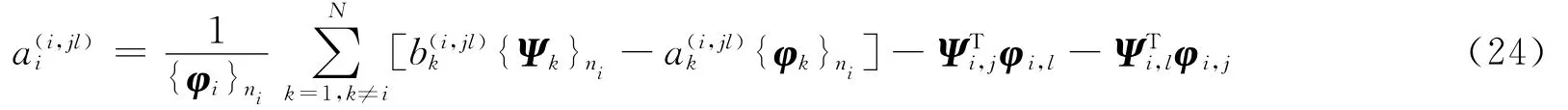
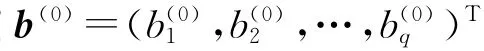
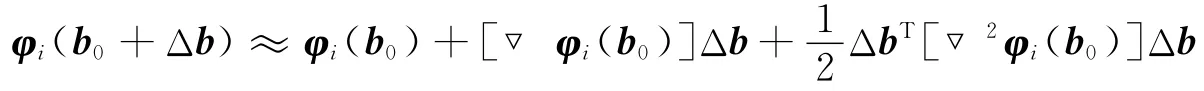
上述公式中所需要的一階導數公式及梯度公式見文獻[7]。
4 結 語
克服了系統的非對稱性的影響,給出了左特征向量的定義,用左特征向量與振型向量的正交性來實現解耦功能。提出了多元向量值函數的海森矩陣的概念及計算非對稱系統的振型向量的海森陣算法,從而構成了系統無阻尼固有振型在設計參數發生擾動后的二階泰勒近似式,為工程應用打下了良好的基礎。
[1] 張淼,于瀾,鞠偉.虧損振系廣義狀態向量靈敏度的移頻算法[J].計算力學學報,2013,30(6):872-878.
[2] 張淼.基于松馳技術的重頻密頻結構模態靈敏度分析[J].合肥工業大學學報:自然科學版,2012,35(12):1605-1609.
[3] 于瀾,張淼,鞠偉,等.非保守系統復模態的規范正交性及其應用[J].華南師范大學學報:自然科學版,2013,45(4):21-24.
[4] 張淼,鞠偉.計算各種振系模態靈敏度的統一算法[J].長春工程學院學報:自然科學版,2012,13(4):119-122.
[5] 于瀾.模態參數的靈敏度分析在結構工程領域中的應用[J].長春工程學院學報:自然科學版,2012,13(3):1-3.
[6] 李德葆,陸秋海.實驗模態分析及其應用[M].北京:科學出版社,2001:79-81.
[7] 張淼.實模態的梯度矩陣算法[J].長春工業大學學報:自然科學版,2013,34(5):551-554.

