兩類Witten-Laplacian算子Dirichlet邊值問題的第一特征值*

鄧義華，肖 娟，李元旦

(衡陽師范學院數學與計算科學系，湖南 衡陽 421008)

假設(M,g)是Rieman流形，f是(M,g)上的光滑函數，那么在(M,g)上有一類重要的Witten-Laplacian算子, 其定義為

Δf=Δ-▽f▽

Witten-Laplacian算子有時也被稱為帶權Laplacian 算子或f-Laplacian算子。目前，這類算子已經得到了許多方面的研究。比如，Chen和Brighton等[1-2]討論了f調和函數的性質，得到了這類調和函數的一些梯度估計。Dung等[3-4]利用f-Laplacian 算子的第一特征值λ1刻畫了f調和函數的性質以及流形(M,g)的度量性質。Chen等[5-6]得到了Witten-Laplacian算子特征值的一個比較定理。利用該比較定理，Futaki等[7]討論了當Ric+Hessφ≥Kg時φ-Laplacian 算子第一特征值λ1的下界估計問題，在此基礎上得到了一類緊致Rieman流形直徑下界的一個比較好的下界估計。

假設a，b，d，k都是常數并且d>0，k>0，Ω是Rn上的有界開區域，那么可以在Ω和區間(-d,d)上分別定義以下函數

v(x)=ax+b，x∈(-d,d)

顯然w和v都是光滑函數。由于開區域Ω和開區間(-d,d)都可以看成是Rieman流形，所以我們可以分別在Ω和(-d,d)上考慮w-Laplacian算子Δw=Δ-kx▽和v-Laplacian算子Δv=Δ-a▽。受前面所提這些參考文獻的啟發，本文將進一步討論以上兩類Witten-Laplacian算子Dirichlet邊值問題的第一特征值。通過直接計算不難得到Ric+Hessw=-kg以及Ric+Hessv=0，所以本文相當于針對兩種特殊情況K=-k<0和K=0討論文[7]中的一些問題。這時，我們認為本文的結論應該比文[7]中的定理1.1更好。

1 w-Laplacian 算子Dirichlet邊值問題第一特征值的下界估計

假設Ω是Rn上的有界開區域，在Ω上定義如下光滑函數

在本節，我們將討論w-Laplacian算子Δw=Δ-kx▽的如下Dirichlet邊值問題的第一特征值的估計問題

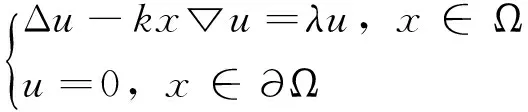
(1)

如果k=0, 那么問題(1)就是通常的Laplacian算子Δ的特征值問題。對Laplacian算子的第一特征值進行估計已經有了很長的歷史，目前在這方面已經取得了很多好的研究成果[8-10]。特別是，在文[8]中已經得到了當流形的Ricci曲率Ric≥0時Laplacian算子第一特征值λ1(Δ)的如下最佳下界估計

(2)

其中d為Ω的直徑。當k≠0時，研究問題(1)的特征值一般是用所謂的加權體積測度e-wdx, 如引言中的大部分參考文獻都是這樣。但是，運用通常的體積測度dx研究(1)的特征值目前似乎還很少有這方面的工作。根據文[3-4]，我們知道f-Laplacian 算子Dirichlet邊值問題的第一特征值可以用下面的式子來刻畫

因此，考慮問題(1)的第一特征值λ1時，我們不妨假設u是Ω上的正函數。為了得到問題(1)的第一特征值下界的更好估計，我們將借用文[7]中的一些方法。為此，我們任取常數α>1，然后將問題(1)中的方程兩邊同時乘以uα-1并進行積分得

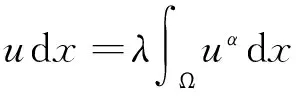
(3)

根據散度定理以及問題(1)中的邊界條件得到

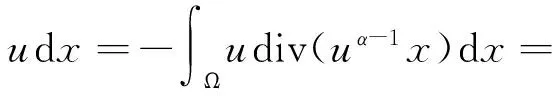
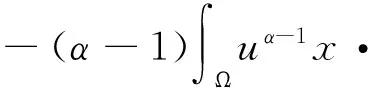
從而有

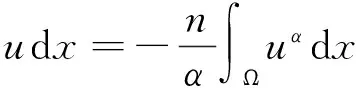
(4)

將式(4)代入式(3), 然后運用分部積分法，可以得到

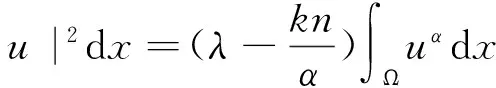
(5)

假設uα=h2，那么4|▽h|2=α2uα-2|▽u|2, 所以根據式(5)不難得到

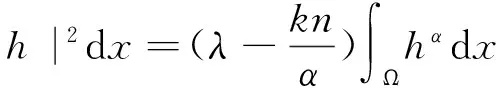
于是

(6)

根據式(2)以及式(5)可得

(7)

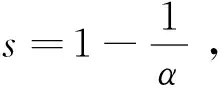
定理1 特征值問題(1)的第一特征值λ1滿足下面的不等式

2 v-Laplacian算子Dirichlet邊值問題第一特征值的準確值

假設a，b，d都是常數并且d>0，v(x)=ax+b，x∈(-d,d)。在本節，我們主要討論v-Laplacian算子Δv=Δ-a▽的Dirichlet邊值問題第一特征值的準確值。為此，我們假設該邊值問題的第一特征值為λ1，相應的特征函數為u。那么，我們有

(8)

證明由二階常系數線性齊次常微分方程的理論可知，當a2>4λ1時問題(8)中的方程的通解為

u=C1ek1x+C2ek2x

(9)

其中

將問題(8)中的邊界條件代入式(9), 我們不難發現C1=C2=0。所以在這種情況下問題(8)沒有非零解。同理可得，當a2=4λ1時問題(8)也沒有非零解。所以只有當a2<4λ1時問題(8)才有非零解，這時問題(8)中的方程的通解為

(10)

將問題(8)中的邊界條件代入式(10)得

(11)

(12)

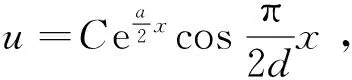
注定理2說明

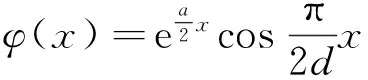
[1] CHEN L, CHEN W Y. Gradient estimates for positive smoothf-harmonic functions [J]. Acta Math Sci, 2010, 30B: 1614-1618.

[2] BRIGHTON K. A Liouville-type theorem for smooth metric measure spaces [J]. J Geom Anal, 2013, 23: 562-570.

[3] DUNG N T, SUNG C J A. Smooth metric measure spaces with weighted Poincaré inequality [J]. Math Z, 2013, 273: 613-632.

[4] DUNG N T. A splitting theorem on smooth metric measure spaces [J]. Arch Math, 2012, 99: 179-187.

[5] CHEN M F, WANG F Y. Application of coupling method to the first eigenvalue on manifolds [J]. Sci Sinica Ser A, 1984, 37: 1-14.

[6] CHEN M F, WANG F Y. General formula for lower bound of the first eigenvalue on Riemannian manifolds [J]. Sci Sinica Ser A, 1997, 40: 384-394.

[7] FUTAKI A, LI H Z, LI X D. On the first eigenvalue of the Witten-Laplacian and the diameter of compact shrinking solitons [J]. Ann Glob Anal Geom, 2013, 44: 105-114.

[8] ZHONG J Q, YANG H C. On the estimate of the first eigenvalue of a compact Riemannian manifold [J]. Sci Sinica Ser A, 1984, 27(12): 1265-1273.

[9] LI P, YAU S T. Estimates of eigenvalues of a compact Riemannian manifold [J]. Proc Symp Pure Math, 1980, 36: 205-239.

[10] WANG Q L, XIA C Y. Isoperimetric bounds for the first eigenvalue of the Laplacian [J]. Z Angew Math Phys, 2010, 61: 171-175.