單擺Duffing振子系統建模及其非線性特性數值仿真分析
劉 魁,李 欣,孫運其
(蘭州交通大學 機電工程學院,甘肅 蘭州 730070)
單擺是處理擺動問題的經典模型.李元杰[1]研究了單擺的自由、束縛及界軌運動,并闡明了單擺系統蘊含著隨機性,一定條件下可以產生混沌.劉延柱、陳立群[2]詳細介紹了非線性振動的研究對象和研究方法,并介紹了關于分岔理論和混沌振動的基礎知識.謝柏松[3]用Melnikov方法研究了具有弱阻尼與參數激勵的單擺及倒擺運動的同宿軌道分岔、次諧分岔和混沌現象.郎和[4]研究了受保守單擺系統中的KAM環面的變形、扭曲、破裂及混沌出現的過程.楊青勇[5]采用相圖方法和龐加萊截面法研究了單擺中分岔、混沌等非線性特征.曹剛等[6]利用雅克比橢圓函數法研究了單擺的線性與非線性運動.何松林等[7]利用平均法研究了弱阻尼條件下的單擺振動.鄧永菊等[8]利用Fortran語言編程,研究了大擺角單擺的非線性振動.但是有關單擺的Duffing振子的動力學問題研究較少,對單擺動力系統具體的分岔分析通向混沌道路的研究也較少,本文以單擺關于Duffing振子的動力學模型為研究對象,利用數值法研究振幅和Duffing振子恢復率對系統動態特性的影響.
1 單擺非線性動力學模型及其微分方程
在單擺模型實驗中,單擺在空氣中來回擺動時,總會受到空氣阻力和其他一些外界因素的作用,因此,在考慮實際的單擺模型時,往往需要考慮外界的作用,我們現在討論小阻尼運動和外加作用力時的情況,當小阻尼運動時,阻力大小和物體速度大小成正比.可以得到運動方程:
兩端同除以ml得到
(2)
(3)
討論非線性振子時,主要討論含有立方項恢復力的非線性振子,為了方便討論,稱之為Duffing振子.
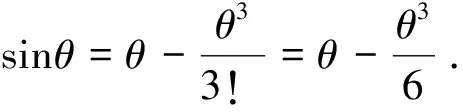
(4)
將式(4)代入式(3),可得:
(5)
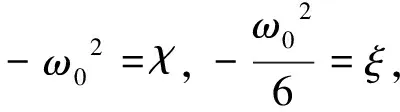
(6)
在任意大振幅下,方程(1)的解變得十分復雜,下面利用計算機模擬,分別討論單擺運動隨其參數變化的周期運動和其混沌運動.
2 非線性動力學特性的分析
將式(6)轉化為狀態方程如下:

(7)
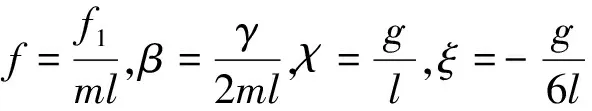
2.1 單擺的外激勵幅值的影響
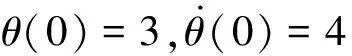
利用Matlab軟件對單擺的動力學狀態方程進行數值求解,系統量綱歸一化后轉角隨振幅f的分岔圖如圖1所示,其相應的Lyapunov指數如圖2所示,由圖2可以看出,當f∈[20,34.2]時,其Lyapunov指數小于0,所以單擺為穩定的的周期運動,當f=20時,系統運動為穩定的周期6運動,當f≥20.8時系統發生逆周期倍化分岔變為周期3運動,但是f≥24.3時系統又發生倍化分岔重又變為周期6運動,f≥26.4時發生逆倍周期分岔系統再次恢復為周期3運動,f=30時系統周期3運動的龐加萊截面圖如圖3(a)所示.當f≥31.5時,系統的周期運動失穩,經周期倍化分岔轉變為周期6運動,f=33時系統周期6運動的龐加萊截面圖如圖3(b)所示.f≥33.9時系統的周期6運動經周期倍化分岔轉變為周期12運動直至f=34.2,當f=34時,其龐加萊截面圖如圖3(c)所示.當f∈[34.2,38.4]時,其Lyapunov指數大于0,系統此時進入了混沌,f=37.5時系統混沌運動的龐加萊截面圖如圖3(d)所示.但是當f≥38.4時系統的Lyapunov指數小于0,結合分岔圖可知系統由混沌運動再次進入穩定的周期運動,f=40時的系統周期9運動的龐加萊截面圖如圖3(e)所示.總體來說,振幅f不斷增大時,系統經歷了6-3-6-3-6-12周期直至混沌響應的變化,說明由于受Duffing振子恢復率和阻尼的影響,當振幅變化時,系統由倍周期分岔通向混沌運動.
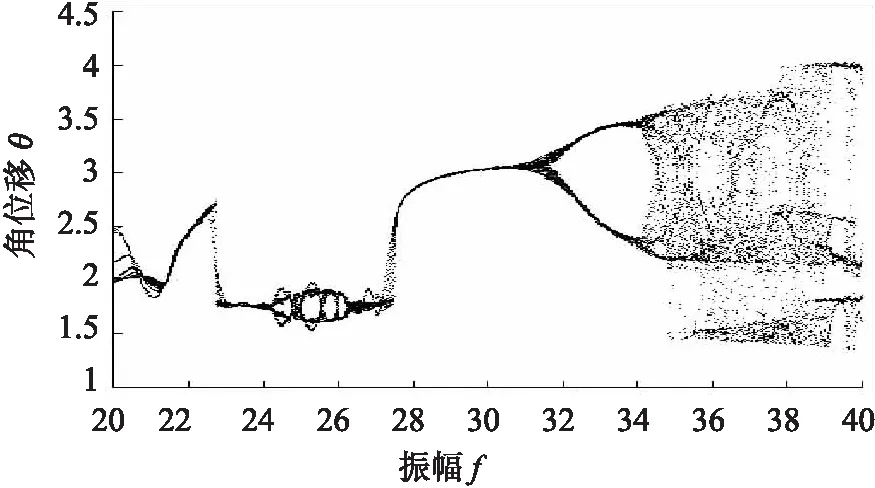
圖1 角位移隨振幅f的分岔圖

圖2 振幅f的Lyapunov指數

2.2 單擺的Duffing振子恢復率影響
其他參數與上節相同,保持參數f=37.5,改變Duffing振子恢復率ξ的值,分析系統動態響應的變化.
Duffing振子恢復率ξ的分岔圖和Lyapunov指數圖如圖4~5所示,從圖中可以看到,當ξ∈[0.2,0.83]時,系統的Lyapunov指數小于0,所以系統為穩定的周期運動,ξ=0.2時,系統為穩定的周期3簡諧運動,ξ=0.3時系統周期3運動龐加萊截面圖如圖6(a)所示,ξ>0.43時,系統由周期3運動變為周期6運動,圖6(b)為ξ=0.45時系統周期6運動的動態響應圖.ξ≥0.51系統發生逆倍周期分岔,系統又有周期6運動變為周期3運動.當ξ≥0.73時,系統又倍化分岔為周期6運動,但是當ξ∈[0.83,1.04]時,系統的Lyapunov指數大于0,系統進入混沌運動,圖6(c)是ξ=1時龐加萊截面圖.ξ≥1.04時,其Lyapunov指數再次小于0,系統又重新進入穩定的周期運動.如圖6(d)所示,當ξ=1.1時處于周期9運動.

圖4 Duffing振子恢復率ξ的分岔圖

圖5 Duffing振子恢復率ξ的Lyapunov指數
3 結論
本試驗利用Matlab對單擺關于Duffing振子的動力學模型進行了數值求解,給出了系統隨參數變化的分岔圖、Lyapunov指數圖,并結合龐加萊截面圖分析了振幅和Duffing振子恢復率變化時,單擺系統復雜的動力學行為.研究發現,隨著系統振幅或者是Duffing振子恢復率的逐漸增大,系統運動經Feigenbaum倍化序列進入混沌運動,然后其混沌運動又退化為周期運動,本試驗的研究結果對工程實際中選擇合理的振幅和Duffing振子恢復率有一定的指導意義.
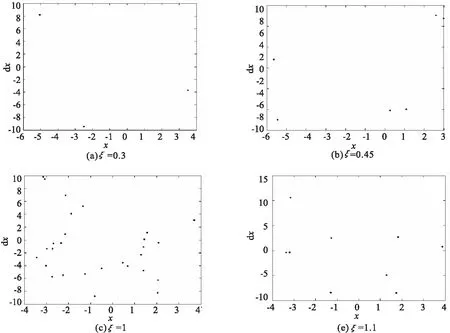
圖6 龐加萊截面圖
參考文獻:
[1] 李元杰.單擺的規則運動及混沌運動的研究[J].大學物理,1998,17(9):6.
[2] 劉延柱,陳立群. 非線性振動[M].北京:高等教育出版社,2001:163-169 .
[3] 謝柏松.單擺運動的同宿軌道分叉、次諧分叉和混沌[J].北京師范大學學報:自然科學版,2000,36(5):631.
[4] 郎和.保守單擺系統中的混沌運動[J].西北師范大學學報:自然科學版,2002,38(4):108-110.
[5] 楊青勇.單擺的混沌運動[J].廣西民族學院學報:自然科學版,2003,9(2):21-25.
[6] 曹剛,任曉蓉,王桂珍,等.單擺的非線性運動[J].山東輕工業學院學報,2006,20(2):82-86.
[7] 何松林,戴祖誠,黃炎.弱阻尼非線性單擺的周期研究[J].大學物理,2009,28(8):20-22.
[8] 鄧永菊,王世芳,吳濤.非線性單擺運動的計算機仿真[J].湖北第二師范學院學報,2010,27(2):59-61.

