不同形狀雙矩孔的夫瑯禾費衍射模擬

2014-03-27 02:49:57薛海國

赤峰學院學報·自然科學版 2014年3期

薛海國

（四川理工學院理學院，四川自貢 643000）

不同形狀雙矩孔的夫瑯禾費衍射模擬

薛海國

（四川理工學院理學院，四川自貢 643000）

根據(jù)雙矩孔的夫瑯禾費衍射在屏幕上的相對衍射強度公式，利用matlab軟件模擬不同形狀雙矩孔夫瑯禾費衍射圖樣與強度分布，從而找出不同形狀雙矩孔與衍射圖樣之間的內在規(guī)律.

夫瑯禾費衍射；光強分布；衍射圖樣；雙矩孔

1 雙矩孔的夫瑯禾費衍射強度

如圖所示，衍射平面x0y0與觀察平面xy距離為z,衍射平面上P（x0,y0）點與觀察平面上Q（x,y）點的距離為r，波長為λ的單色平面波垂直入射衍射平面，U0(P)、U（Q）分別表示P、Q點的光場，根據(jù)惠更斯-菲涅耳原理和基爾霍夫對平面屏幕假設的邊界條件，令小孔外的陰影區(qū)內光場為零，基爾霍夫衍射積分公式可表示為[1]

在滿足夫瑯禾費衍射的條件下，則有

上式中F{U0(x0,y0)}表示U0(x0,y0)的傅里葉變換，上式表明觀察平面的場分布正比于衍射平面上出射光場分布的傅里葉變換.根據(jù)光強I正比于|U(x,y)|2，對于不同情況的衍射屏，只要對衍射孔進行積分，理論上可以求出雙矩形夫瑯禾費的衍射光強分布[2].

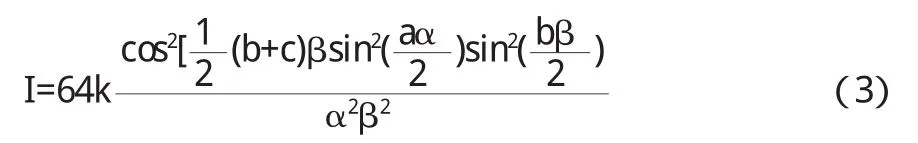
2 不同形狀的雙矩孔在屏上的夫瑯禾費衍射圖樣

根據(jù)公式（3），用matlab軟件，改變矩形的長寬以及兩矩形間距，得到表1所示的圖樣.

3 模擬結果及分析

由表1的10張圖可知，不同形狀的雙矩孔的夫瑯禾費衍射圖樣具有如下特征：

（1）表1中的雙矩孔衍射圖樣，包括特例雙方孔衍射（圖1和圖2）、單縫衍射（圖9）、雙縫衍射（圖8）、單矩孔衍射（圖10），所有的衍射圖樣在上下、左右具有對稱性.明暗相間的衍射條紋與對應矩形的互相平行的兩邊垂直.雙矩孔的衍射可以看成單孔衍射和雙孔干涉共同作用的結果.雙孔干涉的效果體現(xiàn)在橫向和縱向分布的光強主極大中還有若干次極大.衍射圖樣的中央亮斑光強最大，隨著衍射條紋級次的增加，光強依次減弱.

（2）在保持雙矩孔間距不變的情況下，減小某一邊的邊長，與之垂直方向的衍射花樣就變得明顯，如圖1、3、5和圖2、4所示.從圖1、3、5可以看出，如果減小雙矩形豎直方向的長度，其衍射花樣在豎直方向就包含更多的次極大，亮度變大.如果是減小雙矩形橫向的長度，由圖2、4可知，豎直方向的次極大數(shù)目不變，橫向和縱向的衍射條紋變得細長明亮，能觀察到的衍射級次減小.

（3）圖1和圖2是雙方孔衍射花樣，從這兩幅圖可以看出，在保持雙矩孔間距不變的情況下，增大方孔的邊長，衍射花樣變得不明顯，衍射條紋寬度和亮度都減小，但在兩個互相垂直方向上可以顯示更多級次的衍射花紋.

（4）在保持雙矩孔大小不變的情況下，縮小雙矩孔的間距，會讓衍射現(xiàn)象變得明顯，條紋間距變大，如圖5、7和圖6、8所示.

（5）改變矩形孔兩邊長之比，若長邊遠遠大于短邊，衍射圖樣由雙矩孔衍射過渡為雙縫衍射，如圖6、8所示.