大部件對接中基于單位四元數的iGPS測量位姿比對研究

徐碧菡， 孫涪龍， 趙 罡， 邢宏文

(1.北京航空航天大學中法工程師學院，北京 100191；2.北京航空航天大學機械工程及自動化學院，北京 100191；3.上海飛機制造有限公司，上海 200436)

iGPS (indoor GPS)是一種用于大尺寸空間測量與定位的新型三坐標工業測量系統，其工作原理類似于GPS，利用三角測量原理建立三維坐標系，不同的是采用紅外激光代替了衛星(微波)信號。該系統具有測量范圍大、精度高、實時性好、系統安裝方便等特點[1]，并且支持多用戶，即可以使用多個傳感器來完成不同的測量任務，如部件定位、指導機器人工作及同步跟蹤[2]等，具有廣闊的發展前景。目前國內各大航空航天企業已經開始引進iGPS，但對其在飛機裝配過程中的應用仍然處于探索階段。

在大尺寸部件數字化裝配的過程中，運用iGPS進行合理布局，可較為便捷地測得部件關鍵點的位置信息，此時最為關鍵的問題即為對所測數據進行處理并解算出部件的位姿。但由于iGPS實測數據所采用的坐標系統為測量系統定義的局部三維直角坐標系，與理論模型所采用的設計坐標系進行統一后，實測數據點與理論模型并不一致，因此針對iGPS所測數據與理論模型進行位姿比對研究是進一步利用iGPS輔助部件位姿調整的重要前提。

在測量數據與理論模型進行比對的過程中，需要首先實現剛體姿態解算。目前用于剛體姿態解算的方法主要有：奇異值分解法、三點法、最小二乘法、七參數法、單位四元數法等[3-5]。其中，奇異值分解法雖然求解結果較為準確，然而其應用前提為假設質點經過坐標轉換后完全重合，實際在大部件對接中，由于測量誤差的存在，質點經過坐標轉換后不完全重合，從而影響精度；三點法只適用于不共線的3個點，不適用于iGPS同時測量多個關鍵點的使用條件；最小二乘法精度受初始值影響大[3]；七參數法在實際使用過程中涉及針對較小旋轉角度的線性化[4]，因此若旋轉角度較大，就會產生較大的誤差，不適宜用于大部件對接過程中的剛體位姿描述；單位四元數法描述剛體的旋轉與平移變換直觀明了，可針對多點進行計算[5]，并且具有無奇點、不涉及大量三角函數計算等優點，具備作為大部件對接過程中剛體姿態描述方法的條件。

本文根據iGPS本身測量數據的特點，對測量數據的不同形式進行分析與選擇，并根據多點同時測量、大旋轉角等測量要求，提出一種基于單位四元數的測量數據與理論模型位姿比對計算方法，最后通過實驗對該算法進行了分析與驗證。

1 大部件對接中的iGPS測量

iGPS由激光發射器、傳感器、手持探頭、接收器電路和系統軟件組成。測量時，發射器產生兩個激光平面在工作區域內旋轉，轉速約為3000 r/min。接收器根據其所能接收到的激光信號，對水平角與垂直角進行測量[6]。

iGPS的測量數據以Frame為單位。Frame與坐標系類似，每個Frame可包含6個自由度信息，即3個方位自由度信息與3個位置自由度信息。但根據測量前用戶對Frame中所包含傳感器個數及相對位置的不同設定，Frame的自由度信息也會不同。例如，僅包含由單個傳感器返回數據的Frame，只包含點位信息，即3個位置自由度信息；包含兩個相距固定距離的傳感器所返回數據的Frame具有5個自由度信息；而包含4個相對位置固定的傳感器(且其中至少3個傳感器不共線)所返回數據的Frame，則包含6個自由度信息，即由iGPS底層數據處理軟件Surveyor擬合得出的Frame整體的位置與姿態信息。

使用iGPS進行對大部件上多個測量點進行數據測量時，根據Frame的不同數據結構，有兩種數據形式可以選擇，分別為點位測量與位姿測量。點位測量僅包含3個位置自由度信息。當對多個測量點分別布置單個傳感器，并將每個傳感器所測數據設定為單獨的Frame時，得到的測量數據是每個傳感器幾何中心的位置坐標。而位姿測量則需將Frame設置為由多個相互位置固定的傳感器(且至少3個傳感器不共線)及其所測數據構成的整體，得到的數據是由Surveyor經過數據融合計算得出的Frame坐標系原點位置和三坐標軸信息，以及各個點在Frame坐標系下的坐標，但無法獲取每個傳感器所測的原始數據。

在實際測量過程中，點位測量與位姿測量分別有各自的優點與不足。點位測量形式的優點為可直接采用測量點的原始數據進行計算，并根據實際情況有針對性地設計位姿標定算法；缺點為計算過程可能較為復雜。位姿測量形式的優點為可以直接方便地獲取對應Frame的位置與姿態，即測量目標的位置與姿態；缺點為該位姿標定過程由Surveyor自動完成，計算過程涉及多次數據融合，用戶難以針對實際測量情況控制位姿標定過程，誤差分析較難進行。

因此，本文為避免由系統自身多次數據融合所帶來的誤差，采用點位測量形式來配置Frame數據結構，即測量各點的位置坐標信息(3自由度)，并以此為基礎設計適用于飛機對接過程的模型位姿比對算法，為后續的部件對接提供輸入值。

2 基于單位四元數的iGPS測量數據位姿比對算法

將所測點位數據導入理論模型設計軟件后，iGPS測量坐標系與理論模型的全局坐標系重合，便可獲知在同一坐標系下，兩對接部件各自的理論位姿與實際位姿。此時應首先求解部件實測點位信息與理論模型對應點位信息之間的對應關系，即求解兩組一一對應點之間的坐標轉換關系。根據前文對目前幾種常用姿態解算方法的分析，本文采用單位四元數法描述部件姿態。

2.1 基于單位四元數的坐標轉換方法

設初始點集為A，目標點集為E，其中目標點與參考點數目相同、一一對應。若每個點集中點數為k，則可記A={ai}，E={ei}，i=1,2,…,k。計算兩組一一對應點的坐標轉換關系，即為求解滿足：

的最佳旋轉矩陣R與平移向量T。

根據剛體定點轉動理論中的歐拉定理：剛體繞固定點的任一位移，都可由繞過此點的某一軸轉過一個角度得到。假設坐標系OXYZ下該旋轉矩陣對應剛體在三維空間中繞單位轉軸向量v=(ax,ay,az)旋轉θ角，則基于單位四元數的坐標轉換方法思想[6]如下：

假設旋轉轉換向量為單位四元數

其中各分量分別為[7]：

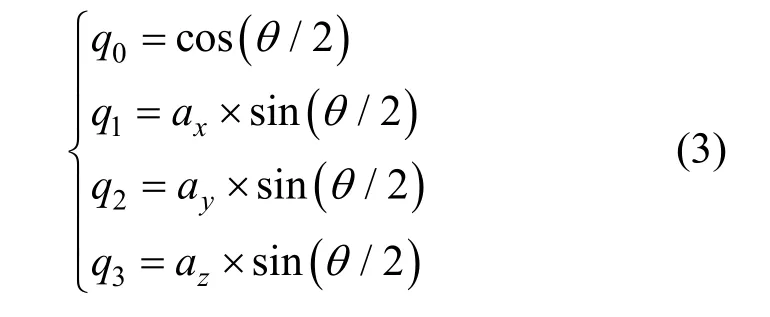
且各分量滿足：

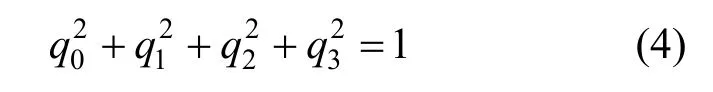
則根據單位四元數可得到3×3的旋轉矩陣R(qR)[8-9]：

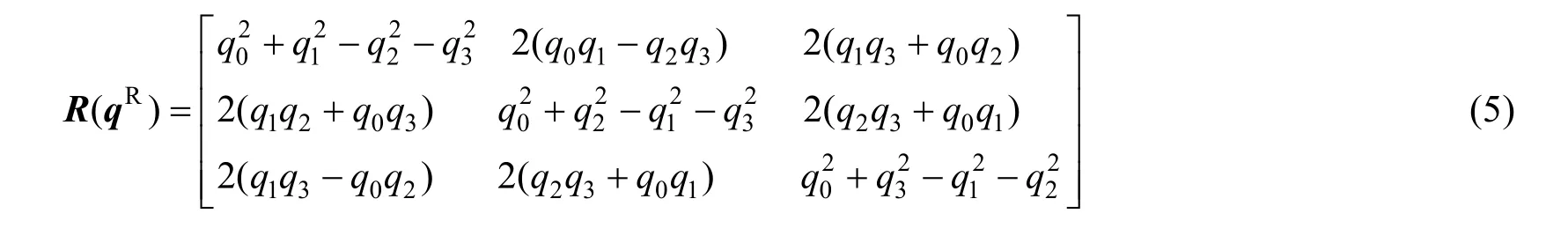
設平移向量為：

則完整的坐標變換向量即為：

考慮到飛機部件尺寸大剛性差的特點，難以做到坐標轉換后與模型完全重合，根據式(1)，結合最小二乘原理設計優化函數如下：

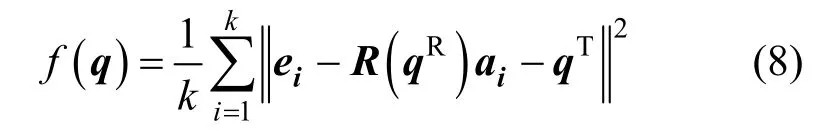
至此求解對應點集間的最佳坐標轉換向量問題轉化為求使得f(q)具有最小值的坐標轉換向量q。

分別求出初始點集A與目標點集E的重心：

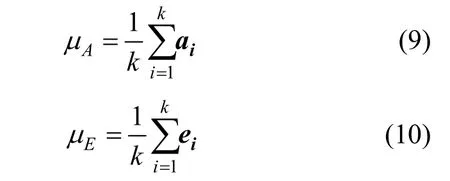
由集合A與集合E構成協方差矩陣：

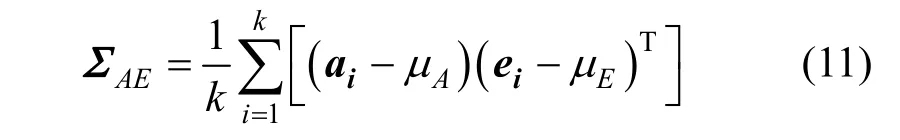
然后利用反對稱矩陣：

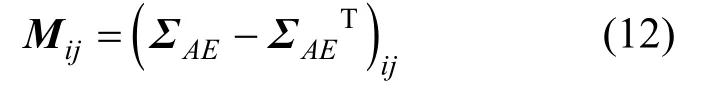
的輪換對稱項來構成列向量：

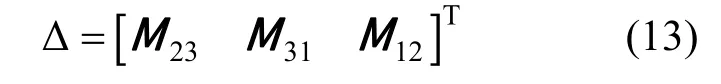
并進一步構造用于求解最優旋轉變換向量的矩陣Q(ΣAE)[8]：

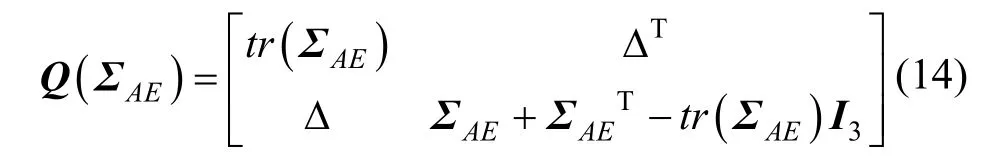
其中，I3為3×3的單位矩陣，tr(ΣAE)為矩陣ΣAE的跡。對應Q(ΣAE)取最大特征值的特征向量qR=[qqqq]T即為最優的旋轉變換向量。因此，最優的平移向量為：

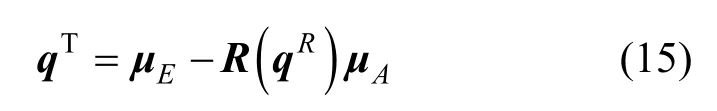
至此，旋轉矩陣與平移向量求解完畢，即可實現坐標轉換。旋轉矩陣所對應的旋轉軸v與旋轉角度值θ可結合式(3)計算得出。

2.2 iGPS測量數據與理論模型比對方法

假設理論模型中，給定兩對接部件M、N，其中M為固定部件，N為移動部件。M與N分別對應于實際部件M′與N′。測量時分別在M′與N′上選定并布置m與n個測量點(m≥3，n≥3)，m與n之間無相互約束關系，可視實際測量需求而定。

首先考慮固定部件，由于其理論模型M在設計坐標系下所有坐標點的信息已知，則可獲取設計坐標系下m個測量點的理論坐標信息；實測部件M′上所布置的m個測量點的坐標信息通過iGPS實測獲得。此時便有了兩組一一對應的坐標值，可采用2.1節中的基于單位四元數的轉換方法計算其轉換關系Q。此處涉及的轉換為將理論模型M上的m個點轉換到實測部件位置。

其次考慮移動部件，確定在實際部件N′上的n個測量點后，通過iGPS實測獲取相對應的n個坐標點信息。此時由于根據第一步中求出的轉換關系Q，即可對移動部件理論模型N上的n個坐標點進行同樣的坐標變換，從而求出實際測量場地中移動部件N′的目標位置N′′。

至此確定了移動部件的實際位置N′與目標位置N′′，即可再一次運用2.1節中所介紹的基于單位四元數的坐標轉換方法，計算出移動部件到達目標位置所需的坐標轉換關系P，從而為后續調姿步驟提供輸入數據。

該方法的具體實現流程如圖1所示。

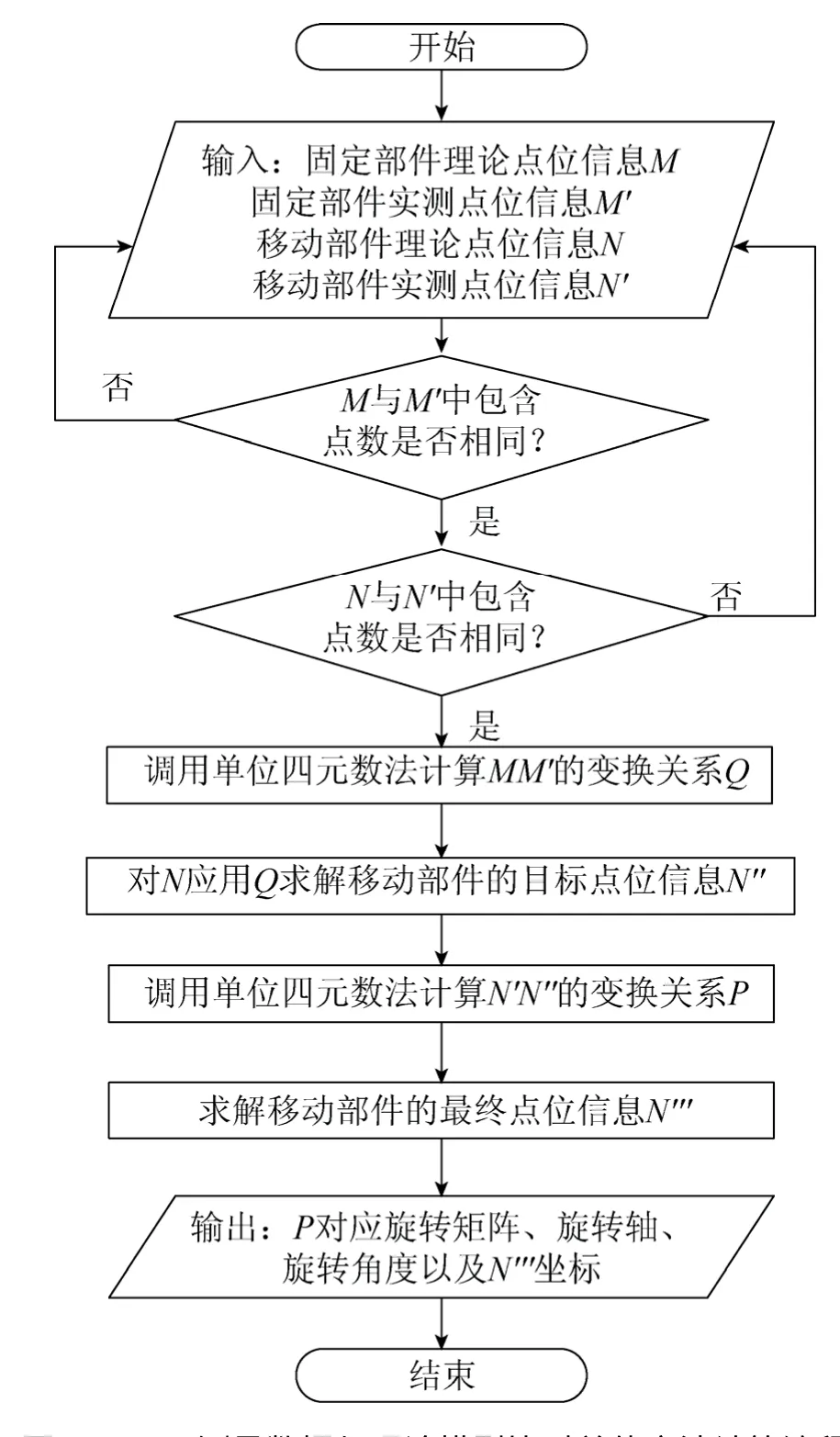
圖1 iGPS測量數據與理論模型比對總體方法計算流程

3 實驗與分析

3.1 驗證實驗方案

為驗證本文提出的基于單位四元數的iGPS測量數據位姿比對算法的精確度，設計驗證實驗。整體思路為，首先根據兩對接部件實測點位信息與理論點位信息計算相關坐標轉換關系；接著在理論模型中兩部件對接面上取3個既屬于固定部件又屬于移動部件的點，用于驗證，理想情況即為：計算得到的移動部件目標位姿上的這3個點，與固定部件實測位姿上的這3個點基本重合；于是對這3個點分別應用第一步擬合得出的坐標變換關系，得出固定部件上此3點的實際位置信息，和移動部件上此3點的目標位置信息，計算這兩組位置信息之間的誤差，考察2節中所提出算法的精度。

具體實驗過程如下：

(1) 首先為實際固定部件與移動部件分別選取m個與n個測量點；

(2) 根據2.1節中坐標轉換方法，由固定部件實測點位信息M′與其理論點位信息M，計算M向M′的轉換關系Q；

(3) 根據式(3)計算Q中單位四元數對應的旋轉軸vQ與旋轉角度θQ；

(4) 根據2.1節中坐標轉換方法，由移動部件實測點位信息N'與其理論點位信息N，計算由N向N′的轉換關系S；

(5) 根據式(3)計算S中單位四元數對應的旋轉軸vS與旋轉角度θS；

(6) 對移動部件理論點位信息N應用轉換關系Q，得到移動部件目標點位信息N′′；

(7) 根據2.1節中坐標轉換方法，由移動部件實測點位信息N′與移動部件目標點位信息N′′，計算固定部件由N′向N′′的轉換關系P；

(8) 根據式(3)計算P中單位四元數對應的旋轉軸vP與旋轉角度θP；

(9) 對移動部件實測點位信息N′應用轉換關系P，得到移動部件最終點位信息N′′′；

(10) 在理論模型中兩部件對接面上取3個驗證點，則這3個點既屬于固定部件，又屬于移動部件。理想條件下對接后固定部件和移動部件上的這3個點應當重合。將此3點位置信息記為MNTest；

(11) 對固定部件對接面上的3個點應用變換關系Q，得到固定部件驗證點的實際位置信息MTest；

(12) 對移動部件對接面上的3個點應用變換關系S，使其到達移動部件實測位置N′附近，得出移動部件驗證點的實際位置信息NTest；

(13) 對NTest的3個點應用變換關系P，得到移動部件驗證點的目標位置信息OTest；

(14) 對比MTest與OTest兩組驗證點的偏差。計算偏差平均值

與標準差σTest。

3.2 實驗數據

下面根據3.1節中的實驗方案進行3組實驗。

為實際固定部件與移動部件分別選取4個測量點，即m=n=4。(實際應用過程中，應根據實際測量點的選取情況確定m與n的取值。)

固定部件理論模型上4個對應點位信息M如表1所示。

移動部件理論模型上4個對應點位信息N如表2所示。

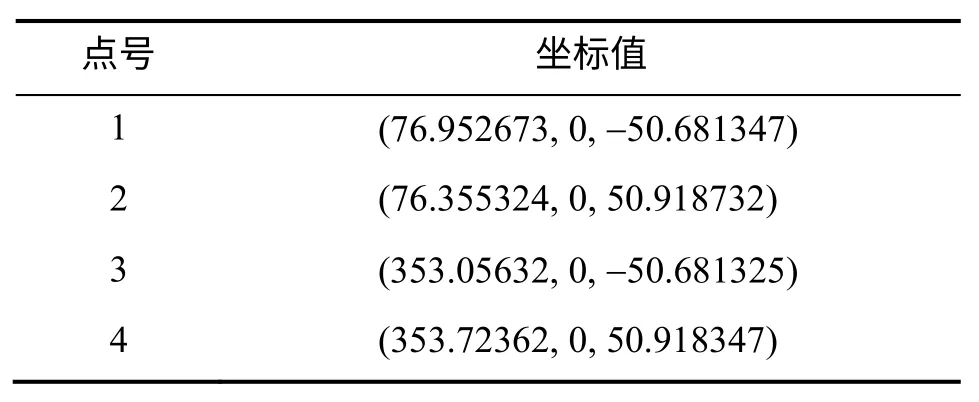
表2 移動部件理論模型對應點位信息N

實驗結果如表3所示。計算過程中涉及的各坐標轉換關系所對應的旋轉軸、旋轉角度、旋轉矩陣以及平移向量結果也均在表中呈現。

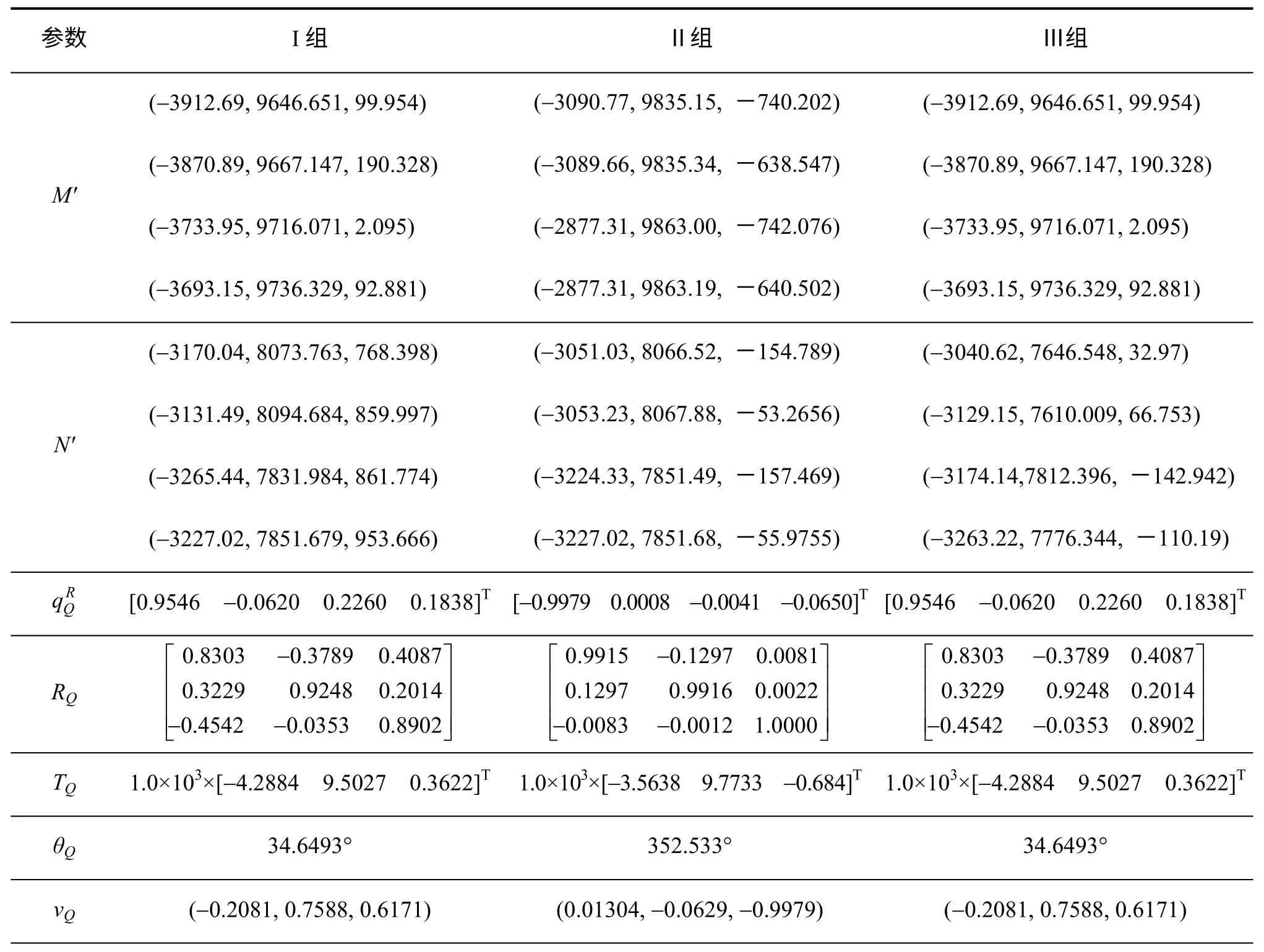
表3 驗證實驗結果

(待續)

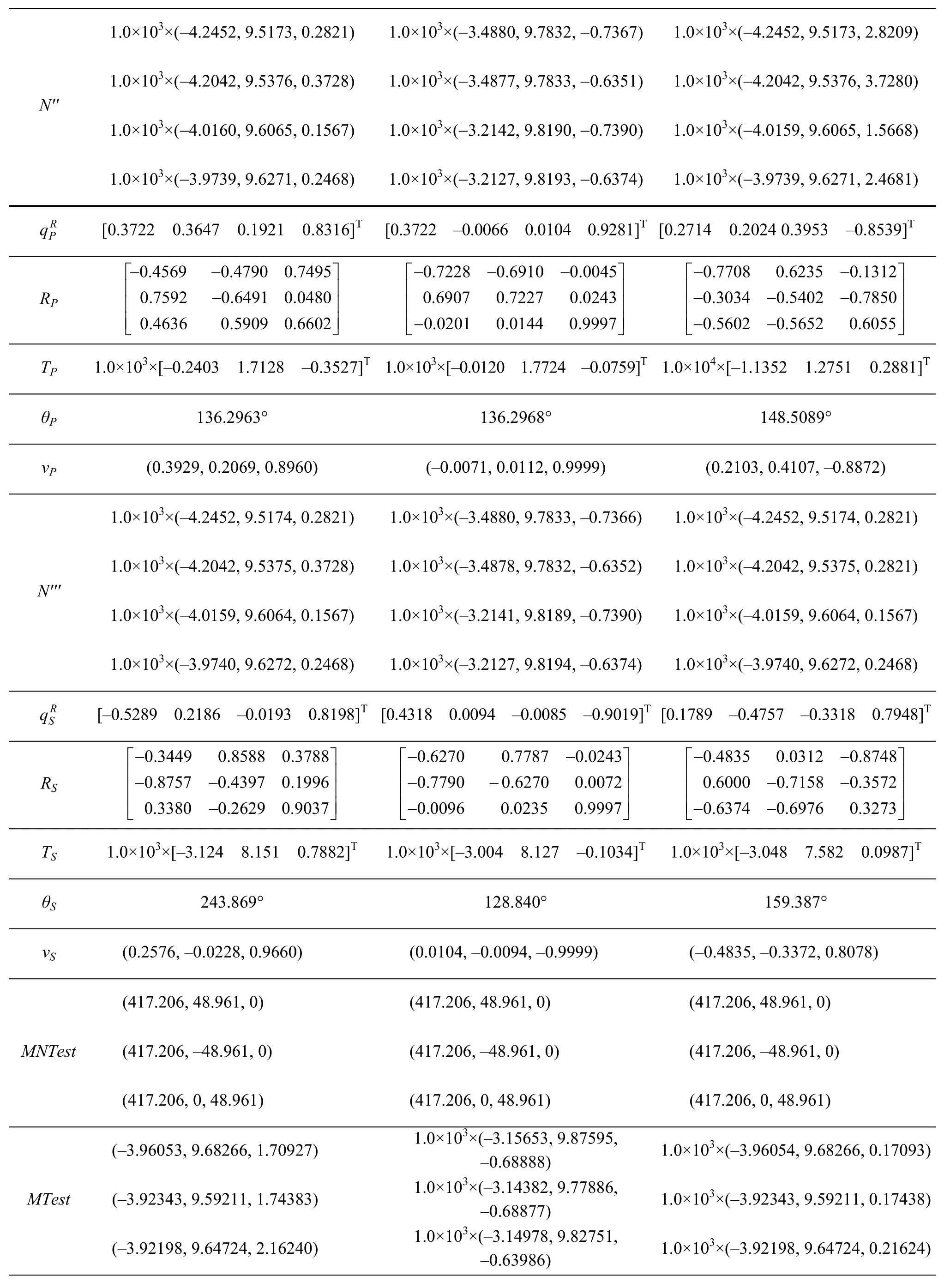
(續表)

(待續)

(續表)

3.3 結果分析

由實驗結果可以看出，在第I組與第Ⅲ組實驗中，固定部件的實際點位信息不變，僅改變移動部件的實際點位信息，因此移動部件由理論模型點位信息向實測點位信息轉動角度以及由實測點位信息向目標點位信息轉動角度都不同，平移向量也不同，但最終驗證點之間的誤差都小于10-11數量級。

第Ⅱ組實驗與第I組相比，則將固定部件與移動部件的實際位置同時改變，但可以看出，無論是大旋轉角還是小旋轉角，坐標轉換的誤差始終小于10-11數量級，標準差也小于10-11數量級。

4 結 論

本文針對大部件對接過程中iGPS多點同時測量、對接旋轉角大的特點，提出了基于單位四元數的iGPS測量數據位姿比對算法，用于部件對接過程中測量數據與理論模型的位姿比對。該算法描述位姿變換簡潔直觀，計算量小，效率高。誤差計算與驗證實驗結果表明，該算法對旋轉角大小和平移量無特殊要求，且在不同條件下均有很高的轉換精度，能有效適用于iGPS的測量位姿比對計算。

[1]呂景亮,張春富,唐文彥,郝欣宇.Indoor GPS 工業測量系統自標定技術研究[J].計量學報,2011,32(1):12-15.

[2]Norman A R,Sch?nberg A,Gorlach I A,Schmitt R.Validation of iGPS as an external measurement system for cooperative robot positioning [J].The International Journal of Advanced Manufacturing Technology,2013,64(1-4): 427-446.

[3]羅 芳,鄒 方,周萬勇.飛機大部件對接中的位姿計算方法[J].航空制造技術,2011,(3): 91-94.

[4]陳 宇,白征東.基于非線性最小二乘算法的空間坐標轉換[J].大地測量與地球動力學,2010,30(2):129-132.

[5]Horn B K P.Closed-form solution of absolute orientation using unit quaternions [J].JOSA A,1987,4(4): 629-642.

[6]吳曉峰,張國雄.室內GPS測量系統及其在飛機裝配中的應用[J].航空精密制造技術,2006,42(5): 1-5.

[7]Yoon D,Narduzzi M,Shen J.Computing rotation minimizing frames using quaternions [J].Computer-Aided Design and Applications,2012,9(5):679-690.

[8]Besl P J,McKay N D.A Method for registration of 3-D shapes [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2): 239-256.

[9]滕志遠,張愛武.單位四元素法在激光點云坐標轉換中的應用[J].測繪通報,2010(11): 7-10.