用于飛機裝配的機構運動學與奇異分析

王 杰，張 霖，田 威

(南京航空航天大學機電學院，江蘇 南京，210016)

采用數字化自動鉆鉚裝備實現飛機大型構件的裝配和聯接是提高裝配效率和質量的有效途徑，也是航空制造業的重要發展趨勢[1-2]。在飛機自動化裝配系統中，要求系統絕對定位精度為±0.5 mm，重復定位精度為±0.15 mm。已有的自動化鉆鉚裝備多采用“C”型布局機床和關節型機器人自動化裝配系統。“C”型機床精度高、剛性好，但體積龐大、成本高且相對工作空間小[3-4]；關節型機器人具有結構簡單、工作空間大、操作靈活等優點，但剛度和精度低，難以滿足鈦合金、復合材料等難加工材料的高效、高質量加工[5-6]。因此，迫切需要有另外一種機構形式的機器人以供選擇。與串聯結構相比，并聯結構具有剛度大、精度高等優點，但其靈活度差、工作空間小。由并聯結構和串聯結構組成的混聯機器人，具有結構簡單、工作空間大、剛度高和動態性能好等優點[7]，其中最有代表性的有Tricept機器人和Exchon機器人[8-10]。以Tricept機器人為例，其精度是一般工業機器人精度的10倍，位置精度能達到±0.2mm，重復定位精度能達到±0.02 mm。因此，混聯機器人越來越受到飛機制造商的關注，國外航空企業已開始運用混聯機器人作為飛機自動化裝配系統。

1 自由度分析

1.1 機構模型及坐標系的建立

圖并聯機構模型

圖并聯機構結構簡圖

1.2 自由度分析

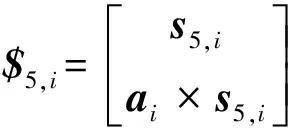
(1)

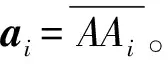
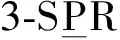
(2)

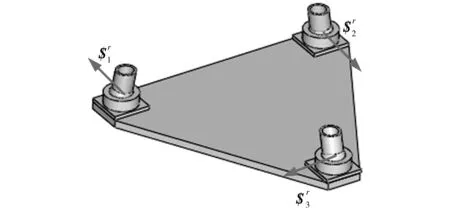
圖3 動平臺所受約束力螺旋

2 位置逆解分析

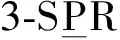
(3)

根據圖2可構造閉環約束方程：

r=bi+Lis4,i-ai(i=1,2,3)

(4)

其中，

ai=Rai0；

注意到支鏈i中轉動副軸線s5,i與ai及s4,i存在相互垂直的幾何關系，故可構造如下約束方程:

(5)

其中，

s5,i=Rs5,i0;

將式(5)展開并整理可得：

sinγcosβ=0

(6)

xcosγcosβ-zsinβ=0

(7)

(x-b)(cosγsinβsinα-sinγcosα)+

y(sinγsinβsinα+cosγcosα)+

zcosβsinα=0

(8)

對式(6)，考慮到β為機構的一個獨立自由度，故有γ=0,于是式(7)和式(8)可簡化為

xcosβ-zsinβ=0

(9)

(x-b)sinαsinβ+ycosα+zcosβsinα=0

(10)

綜上分析可知，給定動平臺中心點A的位置坐標(x,y,z)T便可計算出α、β、γ，進而得到選擇矩陣R。于是各驅動支鏈的長度便可通過下式求出：

Li=‖r-bi-Rai0‖(i=1,2,3)

(11)

3 雅克比矩陣分析

(12)

為求機構驅動雅克比矩陣，將3個驅動支鏈移動副鎖定，則可以得到支鏈i的反螺旋為:

(13)

(14)

另外，式(2)為支鏈的一個約束反螺旋，同理可以構造出約束雅克比矩陣為

(15)

4 奇異位形分析

根據雅克比矩陣，機構發生奇異的條件可以表示為|J|=0，對雅克比矩陣取行列式有

|J|=|Jav||Jaw|-|Jcv||Jcw|

(16)

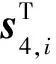
(2)|Jaw|=0。令ni=(a1-L1s4,1)×s5,1，則矩陣Jaw中的元素n1、n2、n3在機構中的矢量表示如圖4所示。從圖4中可以看出，機構在任意位形時都不會出現n1、n2、n3共面的情況，故|Jaw|≠0。因此，機構不會發生此種奇異情況。

圖4 奇異位形

5 運動仿真

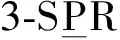
(17)

式中：ρ=100 mm；ω=π/180；z0=800 mm；h=20 mm；t=0∶2∶720。

本文采用Matlab與Solidworks Motion運動仿真軟件相結合的方法來進行機構平臺中心點的運動仿真。首先借助Matlab繪制出三維螺旋線(見圖5)；然后利用Matlab編制機構位置逆解求解方程，求得并聯機構的驅動輸入值L1、L2、L3，并將其加載到Solidworks Motion仿真軟件中進行運動仿真；最后將仿真出的動平臺中心點運動軌跡與Matlab理論軌跡進行比較。

圖5 螺旋線

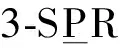
圖6 運動軌跡

6 結語

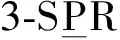
[1] 秦瑞祥，鄒冀華. 工業機器人在飛機數字化裝配中的應用[J].航空制造技術，2010(23)：104-108.

[2] 許國康. 自動鉆鉚技術及其在飛機數字化裝配中的應用[J].航空制造技術，2005(6)：45-49.

[3] 許國康. 大型飛機自動化裝配技術[J]. 航空學報，2008，29(3)：734-740.

[4] De Vlieg R, Feikert E. One-up assembly with robots[J]. SAE International, 2008(1): 22-30.

[5] Summers M. Robot capability test and development of industrial robot positioning system for the aerospace industrial[J].SAE Transactions,2005,114(1):1108-1118.

[6] Bi Shusheng,Liang Jie.Robotic drilling system for titanium structures[J].International Journal of Advanced Manufacturing Technology,2011,54(5-8):767-774.

[7] 陳學生，陳在禮，孔民秀.并聯機器人研究的進展與現狀[J].機器人，2002，24(5)：464-470.

[8] 王友漁，黃田，Chetwynd D G，等. Tricept機械手靜剛度解析建模方法[J].機械工程學報，2008，44(8)：13-19.

[9] 黃真，孔令富，方躍法.并聯機器人機構學理論及控制[M].北京：機械工業出版社，1997.

[10]Neumann K E. Robot: US, 4732525[P]. 1986-03-22.

[11]黃真，趙永生，趙鐵石. 高等空間機構學[M]. 北京：高等教育出版社，2006.