9項人類群體遺傳學特征的對應分析

李玉梅，向 陽，皮建輝

（1.懷化學院數學系，湖南懷化418008；2.懷化學院生命科學系，湖南懷化418008）

人類的一些形態學特征如內眥褶、耳垂類型、頭發類型等明顯地受到遺傳因素的影響，具有群體遺傳特性，在不同民族的人群中存在不同的出現率［1－3］.對這類形態學特征的研究，將為族群的起源以及族群間的親緣關系提供生物學方面的依據，因此這些特征構成了人類群體遺傳學研究的經典指標［4］.近年來，我國學者先后在不同地區對不同群體的人類形態特征的分布頻率及相關性做了廣泛的研究.如：栗淑媛等［2］對內蒙古興安盟3個民族9種形態特征做了相關研究.張興華等［5］對西藏地區13項人類群體遺傳學指標的相關研究.旺慶等［3，6］對浙江漢族和江西漢族9種形態特征做了調查研究.這些研究大多采用相關分析或聚類分析.相關分析只是考察形態特征的相關關系，而沒有體現種族之間的關系；聚類分析只是考察族群間的相近程度，而沒有體現形態特征間的關系.而我們除了要研究族群之間的關系和形態特征之間的關系外，還希望能在同一個直角坐標系內同時表達出族群與形態特征兩者之間的相互關系，實現這一目的的方法是對應分析.

對應分析是一種多元相依變量統計分析技術［7］，通過分析由定性變量構成的交互匯總表來揭示變量間的聯系，可以揭示同一變量的各個類別之間的差異，以及不同變量各個類別之間的對應關系.本文用對應分析研究我國不同地區漢族人群的9項人類群體遺傳學特征.

1 對象與方法

從文獻中整理了6個不同地區漢族的9項人類群體遺傳學特征的出現率，數據見表1.6個不同地區漢族包括浙江漢族［3］，江西豐城漢族［6］，伊盟漢族，巴盟漢族，阿盟漢族和興安盟漢族［2］.9項形態學特征是內眥褶、上眼瞼皺褶、門齒類型、鼻梁類型、鼻孔形狀、下頦類型、耳垂類型、額頭發際、頭發類型.將表1中6個不同地區漢族（Yj，j＝1，2，…，6）作為樣品，9項形態學特征的出現率作為變量（Xi，i＝1，2，…，9），用SPSS13.0軟件對數據矩陣進行對應分析.

對應分析可用于處理二維列聯表資料，具備一般主成分分析的特征.雖要分析的變量較多，但說明問題的只是方差貢獻最大的少數幾個因子.分析中主要取前兩個主成分，要求二者的累計貢獻率較大，一般以大于75%為宜.通過因子負荷圖，能發現各變量與每個樣本的親密程度，每一樣本點或樣本點群，可以用靠近它們的變量點來描述.

2 結果與分析

表2和圖1是6個不同地區漢族9項形態學特征出現率的對應分析中最重要的結果輸出部分.從表2可以看出，前兩個特征值的累積貢獻率為0.917即91.7%，表明這兩個維度能夠解釋總信息量的91.7%，由前二個因子軸構成的二維投影圖（圖1）已包含了原向量信息的91.7%.圖1中，依據各樣品點和變量點的簇集情況，可將它們分成3個點群：

表1 6個漢族9項遺傳學指標出現率Tab.1 Frequencies of occurrence of nine genetic characters of six Han nationalities.／%

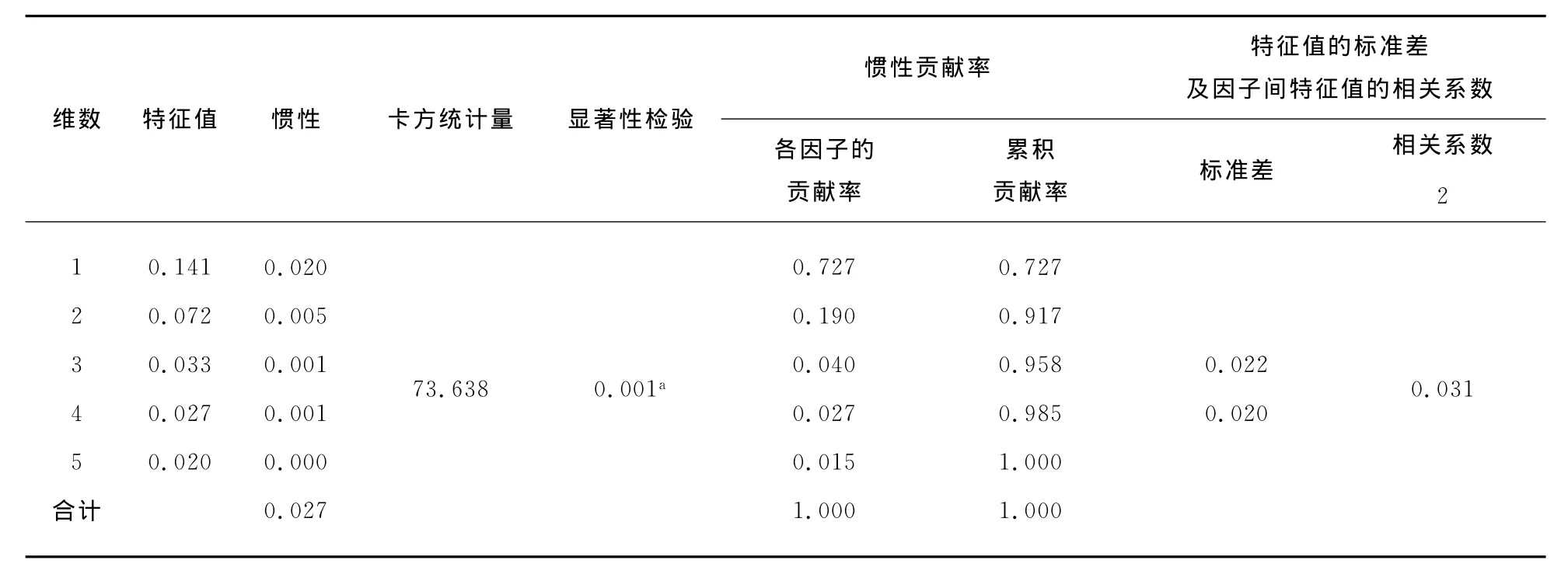
表2 慣性貢獻Tab.2 Inertial contribution

圖1 對應分析因子負荷圖Fig.1 The factor loading chart

Ⅰ.民族：江西漢族 變量：卷發；

Ⅱ.民族：浙江漢族 變量：突形下頦；

Ⅲ.民族：伊盟漢族，巴盟漢族，阿盟漢族，興安盟漢族 變量：有內眥褶，有眼瞼，鏟形門齒，凸鼻梁，窄鼻孔，發際有尖，有耳垂.

點群族Ⅰ江西漢族的卷發出現率最大，為18.1%.相對于其他地區漢族，江西漢族的卷發具有明顯優勢，是其他地區漢族的1～2倍.點群族Ⅱ浙江漢族的突形下頦出現率為43.5%，是其他地區漢族的2～3倍以上，浙江漢族的突形下頦比其他地區漢族更為突出.點群族Ⅲ伊盟漢族、巴盟漢族、阿盟漢族和興安盟漢族，這些民族的有內眥褶，有眼瞼，鏟形門齒，凸鼻梁，窄鼻孔，發際有尖和有耳垂的出現率差異不是特別明顯.

［1］ 王 楊，鄭連斌，陸舜華，等.廣東梅州地區客家人9項人類群體遺傳學指標的研究［J］.華中師范大學學報：自然科學版，2012，46（1）：75－82.

［2］ 栗淑媛，鄭連斌，陸舜華，等.興安盟3個民族9種形態特征的研究［J］.天津師范大學學報：自然科學版，2000，20（4）：39－44.

［3］ 旺 慶，李詠蘭，張瑜珂，等.浙江漢族9項人類群體遺傳學研究［J］.華中師范大學學報：自然科學版，2013，47（3）：380－384.

［4］ 人類遺傳學編寫組.人類遺傳學［M］.北京：高等教育出版社，1999.

［5］ 張興華，鄭連斌，陸舜華，等.西藏林芝地區藏族13項人類群體遺傳學指標的研究［J］.華東師范大學學報：自然科學版，2011，3（2）：152－162.

［6］ 旺 慶，李詠蘭，陸舜華，等.江西豐城漢族9項人類群體遺傳學特征研究［J］.內蒙古大學學報：自然科學版，2013，44（1）：62－68.4

［7］ 裴鑫德.多元統計分析及其應用［M］.北京：北京農業大學出版社，1991.