雙邊帶調制信號間的互相關影響及分析

徐成濤，劉瀛翔，唐小妹，王飛雪

(國防科技大學 電子科學與工程學院，衛星導航研發中心，湖南 長沙，410073)

衛星導航接收機的測距誤差受很多因素的影響，除了噪聲和干擾，目前分析較多的誤差來源包括衛星、接收機的鐘差、電離層延遲、對流層延遲、星歷預測誤差和多徑誤差[1]。衛星導航信號體制的發展體現出向多個頻段、多類服務、多種調制方式的復雜化趨勢。在信號層，出現了新型的導航信號調制方式和復用方式，包括三路信號復用的Interplex 調制[2]和CASM 調制[3]，四路信號復用的AltBOC[4]，TD-AltBOC[5]和Dual QPSK[6]調制、不限定信號路數的POCET 調制[7]。對信號間的相關特性引起的干擾分析，多見于對多址干擾的分析。一般認為，同一頻點的不同衛星信號擴頻碼之間的多址干擾對偽距測量的影響較小。但是李星等[8]指出，在特殊情況下，多址干擾形成的偽碼跟蹤誤差是不可忽略的。而對于同一顆衛星播發的下行導航信號，由于同一衛星的不同信號分量始終具有相同的傳播時延和動態特性，因此，其互相關對偽距測量的影響是固定的，即在任何情況下都可能存在[9]。故相比于多址干擾，互相關會對信號跟蹤產生恒定的影響。但目前還沒有文獻對這類問題進行全面的分析。文獻[9]對同頻的復用信號互相關的影響進行了研究和分析，指出同頻同相的互相關信號將造成一定的互相關影響，其在精密測距場景下帶來的誤差不可忽略。本文作者通過研究指出不同頻信號引入的互相關對偽距測量值的影響，相比于同頻復用信號的互相關是不可忽略的。因此，對于衛星導航系統新體制下廣泛采用的雙邊帶信號如BOC，AltBOC 和TD-AltBOC 等寬帶調制信號，采用單邊帶接收方式時需要考慮對稱邊帶信號引入的互相關問題[10-12]。本文作者首先給出用于信號處理的簡化信號模型，然后對雙邊帶調制信號對接收機跟蹤環路積分結果和測距誤差結果的影響進行分析，最后對前述的理論分析進行仿真測試，驗證雙邊帶信號的互相關確實對信號偽距測量有不利影響，在原有的測距誤差基礎上加入系統偏差。并說明在動態環境下，上述結論依然成立。

1 信號模型

不同復用方式的信號解析表達式存在較大的差異，且相對復雜[13]。根據文獻[9]，本文主要考慮雙邊帶調制信號，即載波頻率不相等的情況。

綜合上述分析后，可以將多路復用信號簡化為

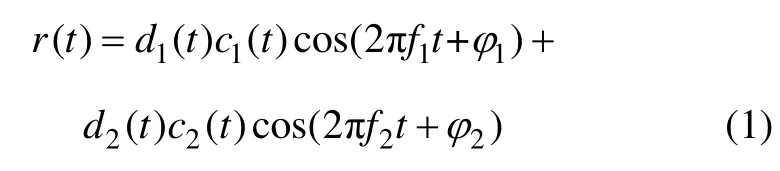
其中：φ 表示兩路載波間的相對相位關系；f1表示目標信號分量的載波頻率；f2表示互相關信號分量的載波頻率；di(t)表示第i 路信號上調制的電文；ci(t)表示第i 路信號上調制的測距碼。

在上述模型的基礎上，分析頻間互相關對信號跟蹤的影響。下面將c1(t)信號稱為目標信號，c2(t)信號稱為互相關信號。

1.1 環路相關器模型

由于接收機一般利用偽距測量值實現定位功能，設接收機已精確復現出接收信號的頻率，接收機生成的本地復現碼與接收信號之間碼相位延遲為τ，早遲碼間隔為2δ，則本地信號和中頻信號相干積分的結果為

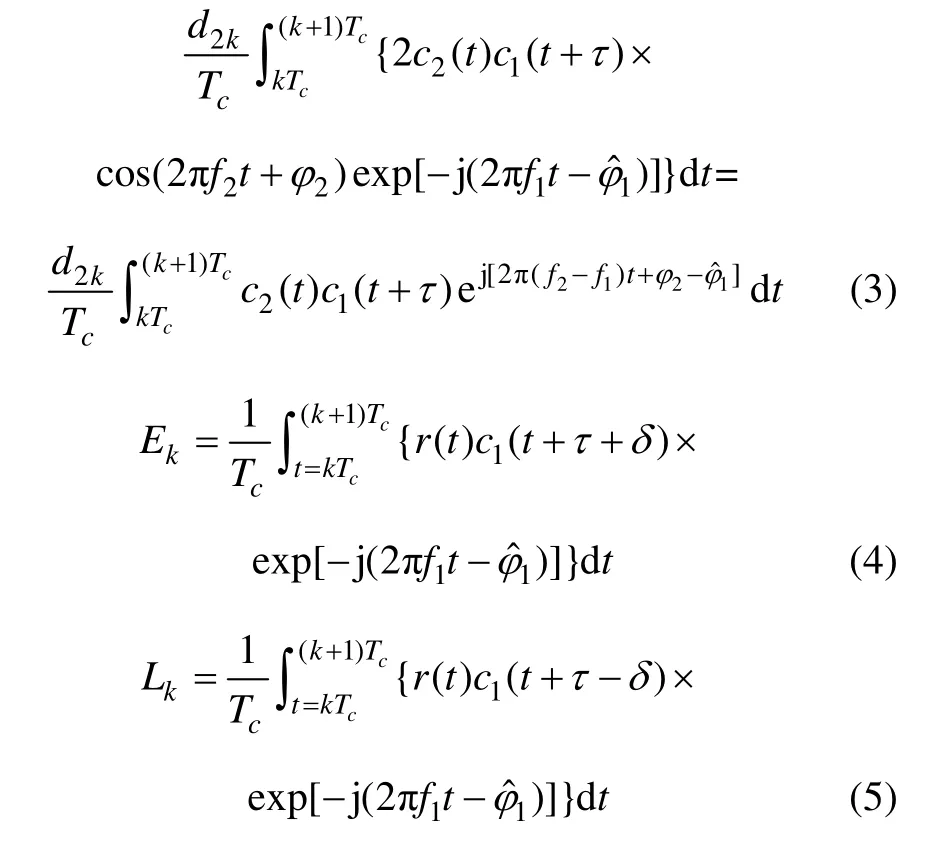
其中：Ek，Pk和Lk分別表示時刻k 對應的提前、即時和滯后支路的相關值，包括同相和正交分量；d1k和d2k分別表示時刻k 對應的電文；Tc表示預檢測積累時間；R11(τ)表示測距碼c1(t)的自相關函數；R12(τ)表示測距碼c1(t)與c2(t)的互相關函數；設Δf=f2-f1，則根據Δf 與積分時間Tc和偽碼速率之間的關系，積分式得到不同的結果。

1.2 鑒別器輸出

偽碼跟蹤環路使用非相干EMLP(提前減滯后功率)鑒別器[14]

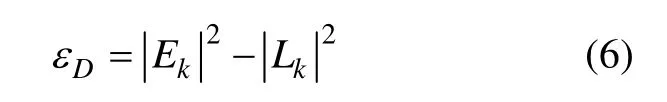
載波跟蹤環路使用Costas環[15]——二象限反正切鑒相器，鑒相器輸出為

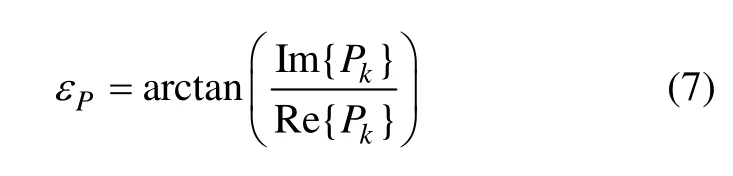
由式(6)和(7)可知：當互相關幅度相比自相關幅度可以忽略時，載波環和碼環穩定的條件為θ=0 和τ=0，即載波環和碼環可以無偏地估計出接收信號的載波相位和偽碼相位。

2 非同頻信號的互相關特性

2.1 當Δf=0 時

該情況下，互相關的影響等于同頻信號分量之間互相關的影響，分析結果見文獻[9]。

此時，DLL 環路相干積分的結果將受到信號間的互相關部分的干擾。

2.2 當Δf＜＜1/Tc 時

此時，載波差頻項在積分時間內的變化緩慢，則載波差頻項可以從積分式中分離[16]，有

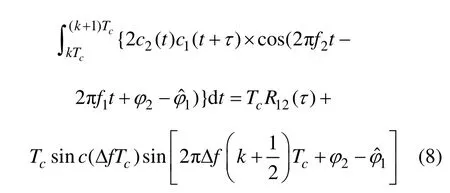
在該情況下，互相關的影響等于同頻信號分量之間互相關的影響。與同頻信號互相關影響的結果類似，此時DLL 環路相干積分的結果將受到信號間的互相關部分的干擾。

2.3 當Δf＞＞max(fcode)時

此時，載波差頻項在偽碼碼片內快速變化，擴頻碼在差頻項的周期內變化緩慢。則可將積分時間分割為載波差頻項周期之和，在該周期內的相干積分為0。則積分器的輸出為

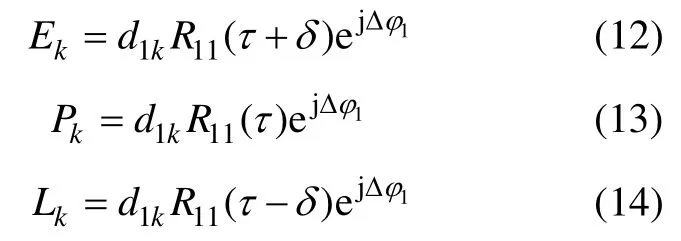
2.4 當Δf 屬于其他情況時

此時，載波差頻與積分時間的倒數可相互比較。此時，該積分不能化簡。

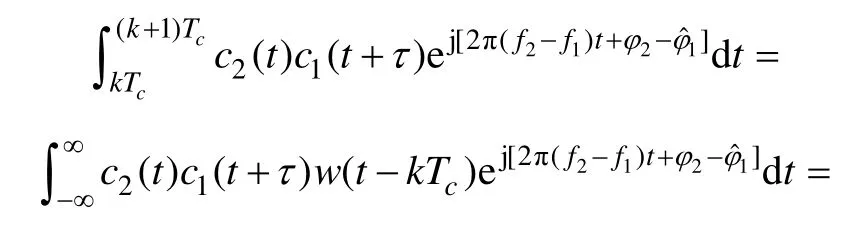
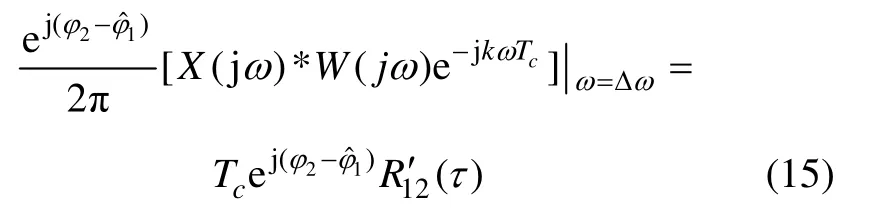
其中：

進一步化簡為

式中：C(jω)為信號的頻譜；*表示線性卷積；R′12(τ)代表廣義下的互相關積分。

值得注意的是，當Δf·Tc為整數時，廣義互相關積分與積分時段k 無關，若Δf·Tc不為整數，則廣義互相關積分在不同積分時段k 下存在相位偏轉，目標信號遭受的互相關影響隨時間變化：

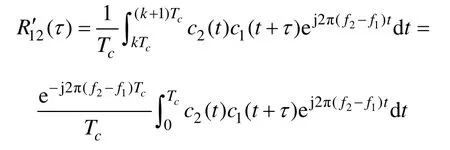
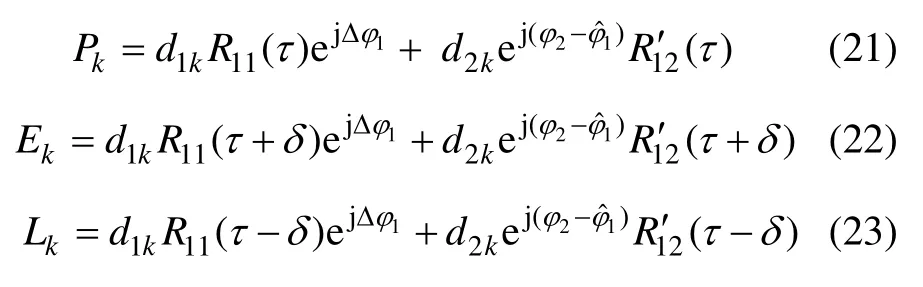
同樣的，DLL 環路相干積分的結果將受到信號間的互相關部分的干擾，由于信號間的互相關無顯式的解析表達式，因此互相關干擾的程度需要采用仿真的方法得到積分的結果。

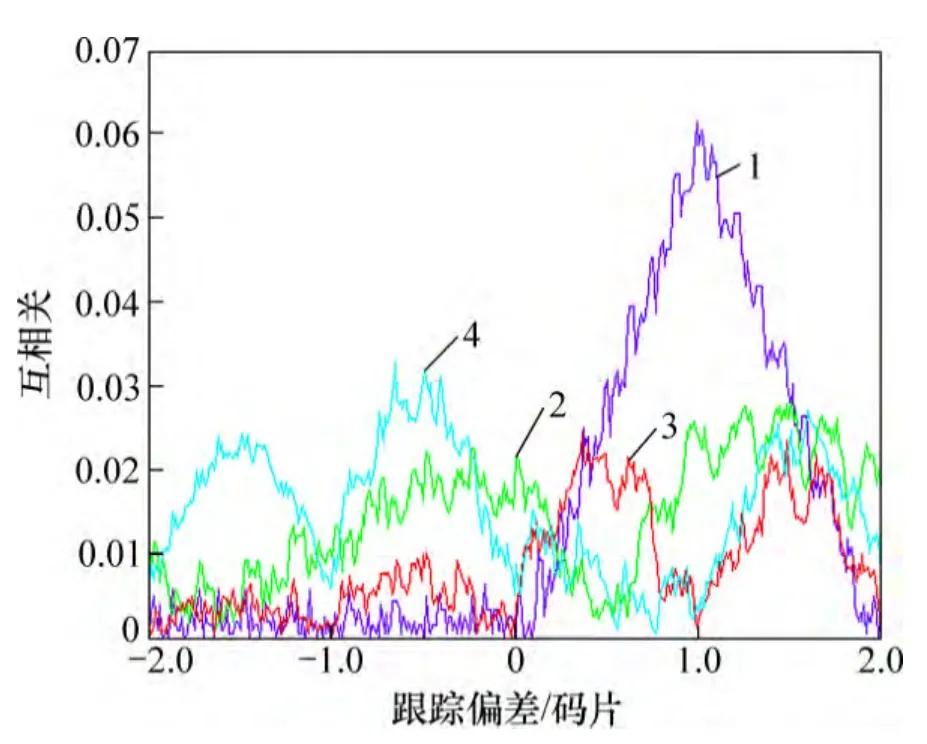
圖1 歸一化廣義互相關積分仿真曲線(PRN1 與PRN5)Fig.1 Simulation curve of generalized cross correlation(PRN1 vs. PRN5)

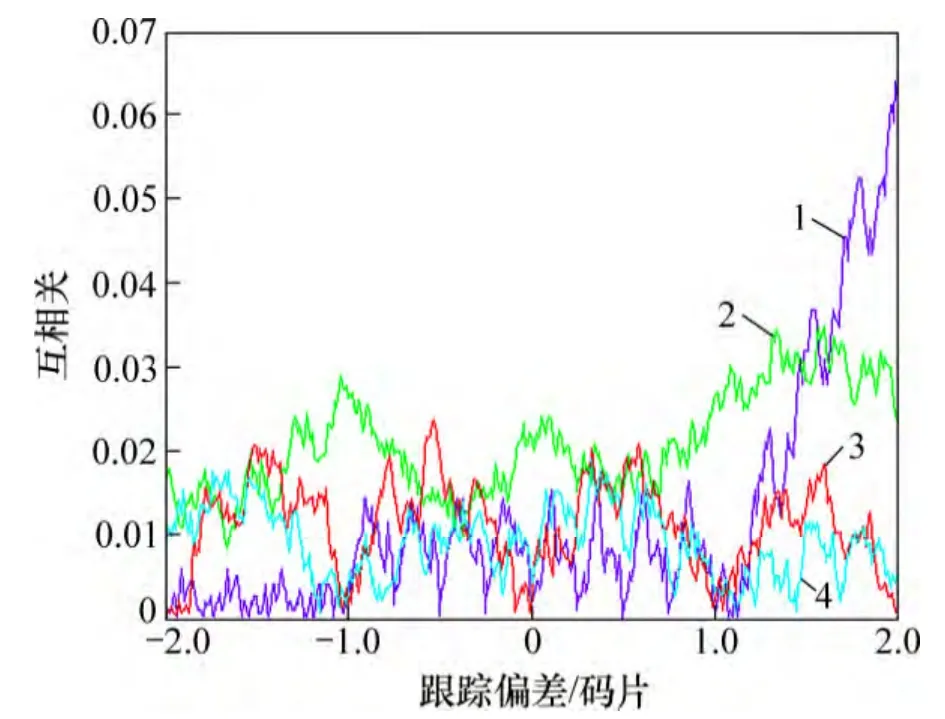
圖2 歸一化廣義互相關積分仿真曲線(PRN1 與PRN2)Fig.2 Simulation curve of generalized cross correlation(PRN1 vs. PRN2)

圖1 和圖2 所示為歸一化廣義互相關積分仿真曲線，其中fc為碼率。從圖1 和圖2 的仿真結果可見：廣義下的互相關積分R′12(τ)有以下幾個特征：(1) 跟蹤偏差小于0.5 個碼片時，互相關積分相比于自相關小1至2 個量級；(2) 互相關積分隨頻差的變化沒有明顯的規律可循，不同頻差下的互相關積分變化不大；(3)通過擴頻碼的設計，可改善零頻下的互相關積分，但廣義互相關積分的改善不明顯。

根據前面對信號模型和延遲鎖定環路相干積分結果的分析，可知根據目標信號與相關信號中心頻率之間的關系，相關器的輸出結果隨之變化。其中，對情況1 和3 的分析已經在文獻[1, 14-15]中論述，而情況2 等價于情況1，下面只考慮情況4 下互相關對跟蹤環路的影響。

3 非同頻互相關對跟蹤的影響

碼環穩定跟蹤時，根據前面的分析，當互相關幅度相比自相關幅度不可忽略時，即除互相關信號的頻差遠大于信號碼率的情況外，互相關信號都將對信號的相關結果產生一定的影響，而一般情況下互相關無法解析表示，因此，無法得到DLL 環路中鑒相器的碼相位延遲τ0的解析解，但是，仍可分析碼相位延遲的近似解及其變化規律。

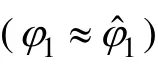
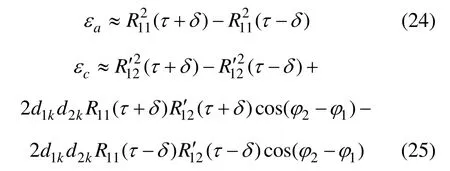
自相關函數可近似表示為：

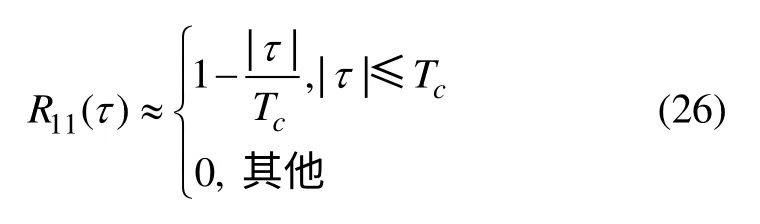
其中：Tc為碼片寬度。可以將信號間的相位關系分為3 種情況：φ=0，例如理想情況下TD-AltBOC 調制中任意2 個的信號分量；φ=π/2，例如理想情況下AltBOC調制中相同邊帶的信號分量；φ 為其他值。在一般情況下，但是由于色散效應和前面的分析，非同頻間的相位差是不可預知的。

當φ2-φ1=π/2 時，因為τ0＜＜δ，因此，碼跟蹤偏差可以根據下式近似得到：

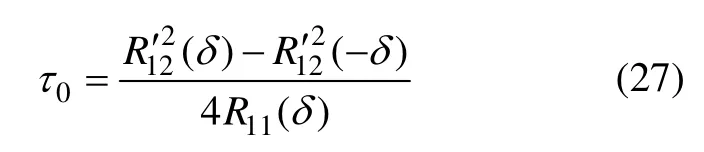
由式(27)可知：當φ2-φ1=π/2，碼跟蹤偏差僅和自相關、廣義互相關、早遲碼間隔有關。

當φ2-φ1=0 時，同樣可以得到該條件下碼跟蹤偏差的解析表達式：

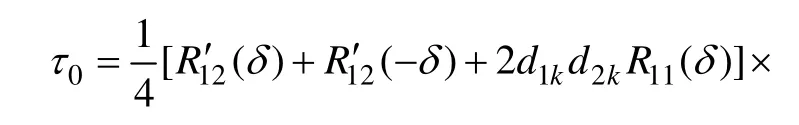
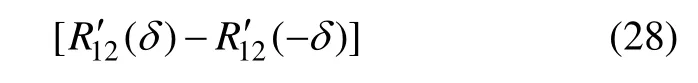
由式(28)可知：當φ2-φ1=0，碼跟蹤偏差不僅和互相關、早遲碼間隔有關，還和調制的電文符號有關。

當φ2-φ1為其他任意值時，碼跟蹤偏差近似為

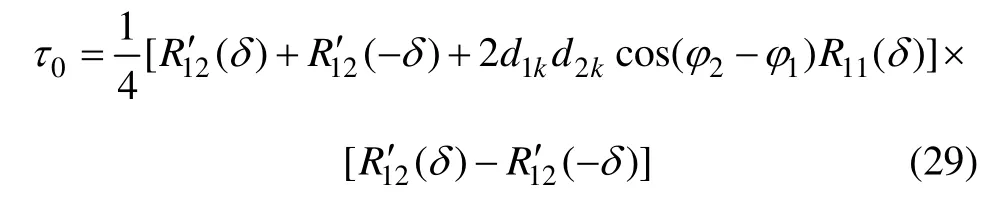
由式(29)可知：此時碼跟蹤偏差不僅與互相關、早遲碼間隔有關，還與調制的電文符號有關。

根據上述結論可知：互相關引入的偽碼相位偏差和電文符號有關。由于真實環境中導航電文在一定的時間段內具有一定的周期性，因此，會造成偽碼相位偏差存在和導航電文周期一致的周期性的波動。

當載波環穩定跟蹤時，載波相位偏差的近似解為

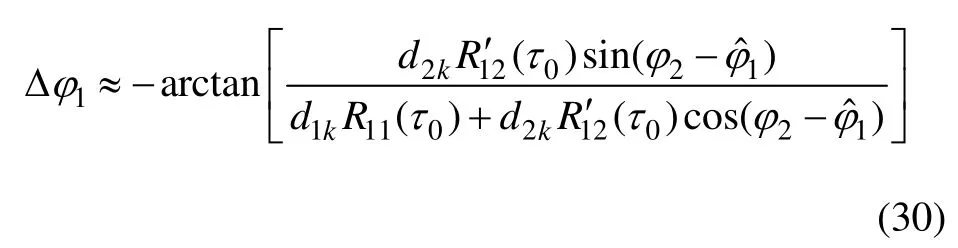
穩定跟蹤時，τ0固定，若此時R′12(τ0)=0，則載波相位偏差近似為0。否則，當滿足以下條件載波相位偏差最大。

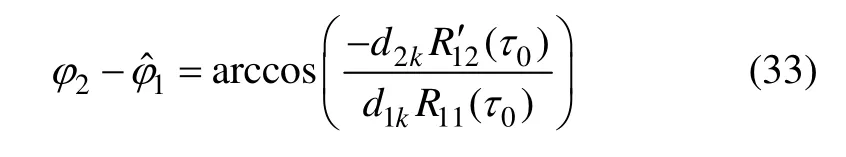
從上面的分析可見：互相關引入的載波相位偏差主要與互相關有關，當目標信號和互相關信號載波同向時互相關對載波相位偏差的影響可以忽略。

4 仿真驗證

下面使用matlab 仿真驗證上述的結論，具體的仿真參數如表1 所示。

由圖3 和4 可見：

(1) 當互相關信號與目標信號存在可與碼率相比擬的頻差時，雙邊帶調制信號的偽碼相位偏差仍然存在，且相比同頻情況沒有明顯的下降趨勢，甚至可能增大；

(2) 同頻時，TD-AltBOC 調制的偽碼相位偏差明顯大于AltBOC。當存在頻差時，TD-AltBOC 調制的偽碼相位偏差和AltBOC 調制的偽碼相位偏差的關系無規律可循。

(3) φ2-φ1=π/2 時，偽碼跟蹤偏差隨電文比特變化而波動，這是由于互相關造成誤差引起了目標信號相干積分跨越了電文比特翻轉時刻，因此，使得碼環不斷地進行調整。通過降低環路帶寬增強濾波效果，可以減少電文比特翻轉帶來的影響。該波動是由互相關間接造成的，但互相關影響較小時，波動不明顯，因此，信號同頻時無明顯波動。當φ2-φ1=0 時，由于電文符號直接影響鑒別器輸出，因此，信號同頻時依然存在跟蹤偏差隨電文波動的情況。

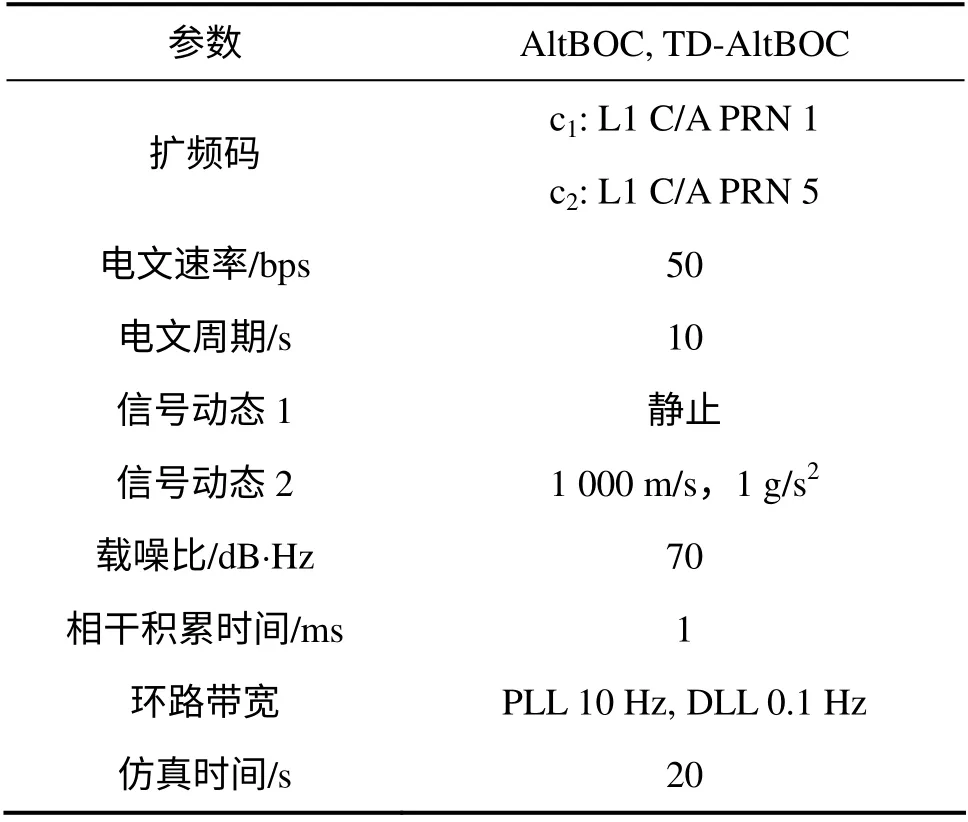
表1 仿真參數列表Table 1 List of simulation parameter

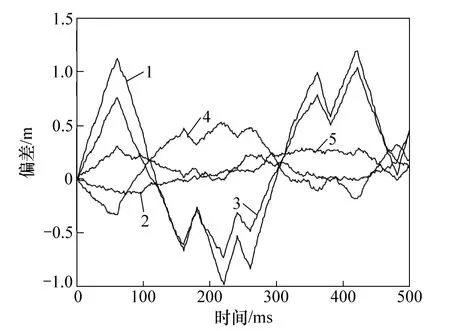
圖3 TD-AltBOC 調制中c1(t)信號的碼相位跟蹤偏差(φ2-φ1=0)Fig.3 Track bias of c1(t) using TD-AltBOC modulation (φ2-φ1=0)

將AltBOC 的互相關信號的c2(t)替換為PRN2，仿真結果如圖5 和6 所示。

由圖5 和6 可見：對于同相或正交的信號，通過選擇同頻下互相關性能更加優異的擴頻碼，在互相關信號與目標信號存在一定頻差的情況下，不易減小互相關引入的偽碼相位偏差。上述結果與前面對廣義下的互相關積分分析結果是一致的。

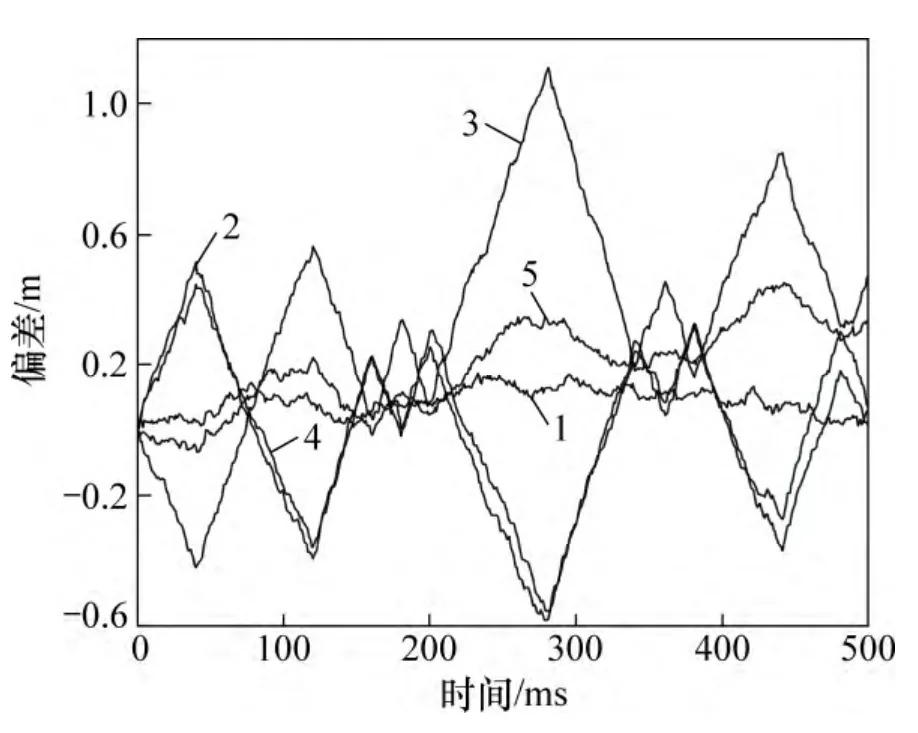
圖5 擴頻碼更換后TD-AltBOC 調制中c1(t)信號的靜態條件下碼相位跟蹤偏差Fig.5 Track bias of c1(t) using TD-AltBOC modulation with different spread codes in static situation

衛星信號動態的變化不會改變互相關和自相關之間的相對關系，因此，互相關對碼跟蹤的影響與靜態情況類似，仿真的結果如圖7 和8 所示。

由圖7 和8 可知：衛星信號動態的變化不會改變互相關信號引入的跟蹤偏差，因此，上述結論對實際環境中的動態信號同樣適用。

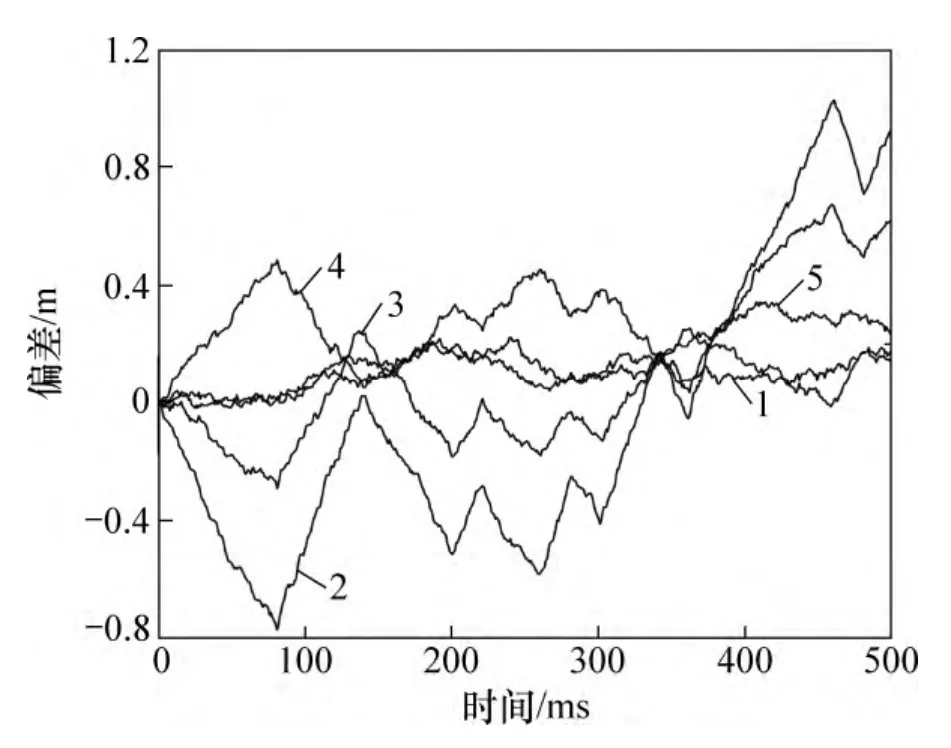
圖6 擴頻碼更換后AltBOC 調制中c1(t)信號的靜態條件下碼相位跟蹤偏差Fig.6 Track bias of c1(t) using AltBOC modulation with different spread codes in static situation

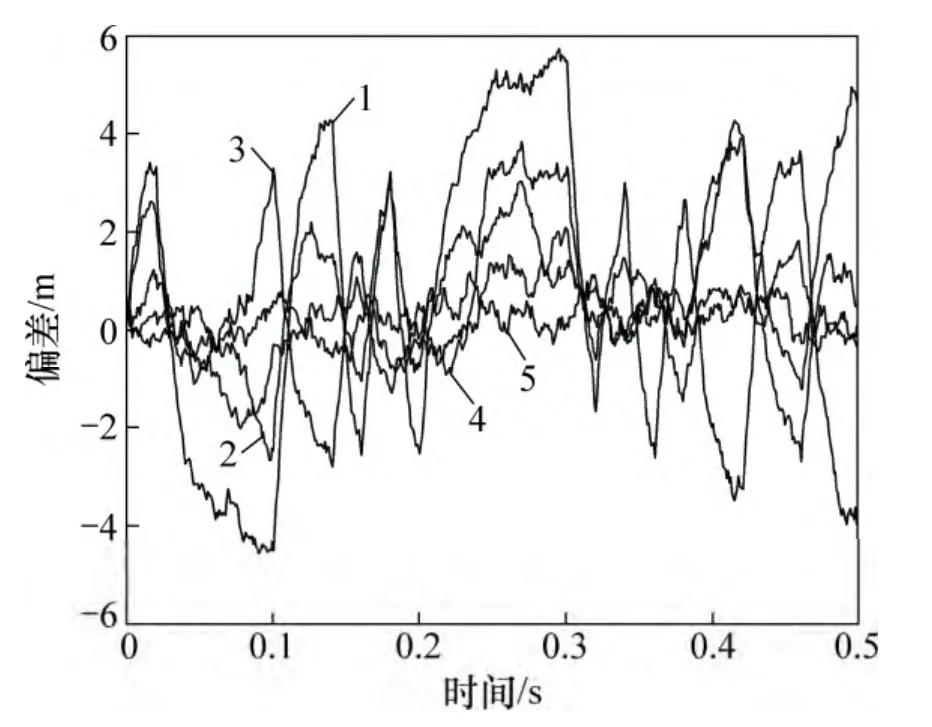
圖7 擴頻碼更換后TD-AltBOC 調制中c1(t)信號的動態條件下碼相位跟蹤偏差Fig.7 Track bias of c1(t) using TD-AltBOC modulation with different spread codes in dynamic situation

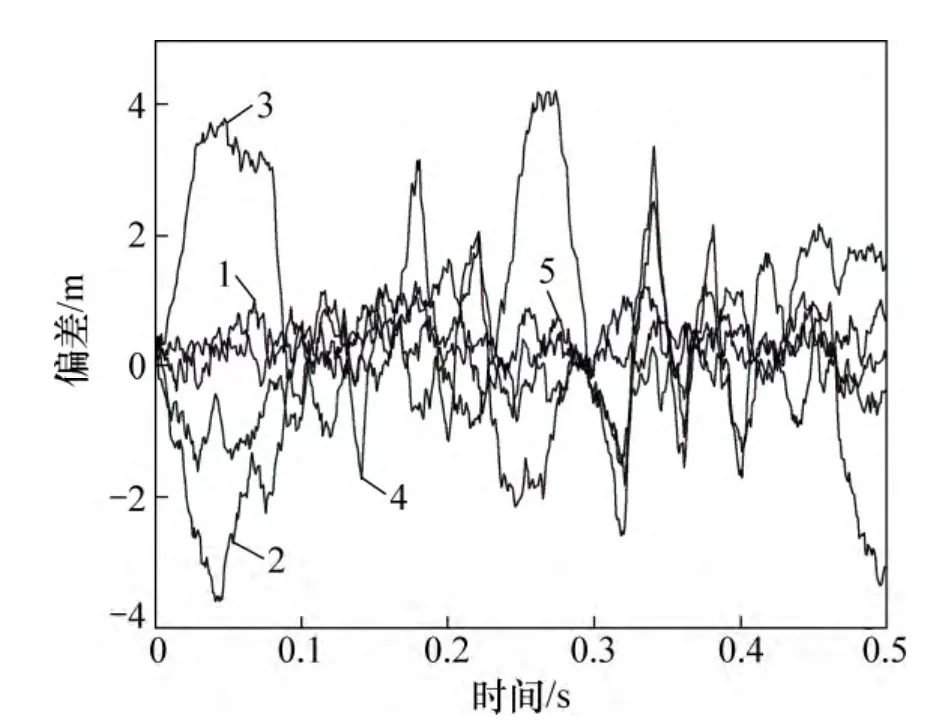
圖8 擴頻碼更換后AltBOC 調制中c1(t)信號的動態條件下碼相位跟蹤偏差Fig.8 Track bias of c1(t) using AltBOC modulation with different spread codes in dynamic situation

5 結論

(1) 隨著雙邊帶信號的頻差變化會有不同的結果。在一般情況下，固定頻差其互相關會引入一定的偽碼跟蹤偏差，而載波相位的變化對跟蹤偏差的影響較小。此外，其他頻點的信號進入中頻數字處理環節后，其互相關同樣會引入較大的偽碼跟蹤偏差。因此采用單邊帶方法處理雙邊帶信號時，需要考慮來自對稱邊帶信號的互相關干擾。

(2) 從減小互相關的影響角度來考慮，AltBOC 調制與TD-AltBOC 相比調制并不更具有優勢。并且在選擇雙邊帶信號的擴頻碼時，需要根據其在±1 個碼片范圍內的廣義互相關值進行擇優選擇，以盡可能減小互相關對偽距測量的影響。該結論對衛星導航系統信號體制的選擇和擴頻碼設計具有一定的指導意義。

[1] 謝鋼. GPS 原理與接收機設計[M]. 北京: 電子工業出版社,2009: 78-90。XIE Gang. Principles of GPS theory and receiver design[M].Beijing: Publishing House of Electronics Industry, 2009: 78-90。

[2] Butman S, Timor U. Interplex: An efficient multichannel PSK/PM telemetry system[J]. IEEE Trans Communication, 1972,20(3): 415-419.

[3] A′vila-Rodr?′guez J A. On generalized signal waveforms for satellite navigation[D]. Munich: University FAF Munich.Faculty of Aerospace Engineering, 2008: 288-290.

[4] Lestarquit L, Artaud G, Issler J. AltBOC for dummies or everything you always wanted to know about AltBOC[C]//Proceedings of 21st International Technical Meeting of the Satellite Division of the Institute of Navigation. Savannah,GA, USA, 2008: 961-970.

[5] TANG Zuping, ZHOU Hongwei, WEI Jiaolong, et al.TD-AltBOC: A new COMPASS B2 modulation[J]. Science China: Physics, Mechanics & Astronomy, 2011, 54(6):1014-1021.

[6] ZHANG Kai. A signal generation method of Dual QPSK: China,201110451739.0[P]. 2011-12-29.

[7] Dafesh P A, Cahn C R. Phase-optimized constant-envelope transmission (POCET) modulation method for GNSS signals[C]//Proceedings of 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation. Savannah,GA, USA, 2009: 2860-2866.

[8] 李星, 王飛雪, 歐剛, 等. 衛星導航系統中多址干擾引起的偽碼跟蹤誤差的分析[J]. 信號處理, 2008, 24(5): 885-888.LI Xing, WANG Feixue, OU Gang. Study on PN code tracking error caused by multi-user interference in satellite navigation system[J]. Signal Processing, 2008, 24(5): 885-888.

[9] LIU Yingxiang, TANG Xiaomei, WANG Feixue. Analysis for cross correlation in multiplexing[C]//China Satellite Navigation Conference (CSNC) 2013 Proceedings. Wuhan, China, 2013:1-5.

[10] Shivaramaiah N C, Dempster A G. A novel extended tracking range DLL for AltBOC signals[C]//Vehicular Technology Conference Fall. Anchorage, Alaska, USA, 2009: 1-5.

[11] Shivaramaiah N C. Enhanced Receiver Techniques for Galileo E5 AltBOC Signal Processing [D]. Sydney: the University of New South Wales. Surveying & Spatial Information Systems,2011: 40-46.

[12] Margaria D. Galileo AltBOC receivers: Analysis of receiver architectures, acquisition strategies and multipath mitigation techniques for the E5 AltBOC signal[D]. Turin: Polytechnic of Turin, Faculty of Engineering Information, 2007: 59-84.

[13] ZHANG Kai. Analytical transmission model of POCET technique for Compass B1 and B3 signals[C]//The 25th International Technical Meeting of the Satellite Division of The Institute of Navigation. Nashville, Tennessee, USA, 2012: 1-8.

[14] van Dierendonck A J. GPS receivers. The global positioning system: Theory and applications[M]. Washington: American Institute Aeronautics and Astronautics, 1996: 329-408.

[15] Kaplan E D, Hegarty C J. Understanding GPS principles and applications[M]. 2nd ed. Beijing: Publishing House of Electronics Industry, 2006: 88-89.

[16] Winkel J ó. Modeling and simulating GNSS signal structures and receivers[D]. Munich: University FAF Munich. Faculty of Aerospace Engineering, 2000: 28-29.