基于JRC-JCS 模型的邊坡局部穩(wěn)定性分析

萬(wàn)世明，吳啟紅，謝飛鴻，楊有蓮

(成都大學(xué) 城鄉(xiāng)建設(shè)學(xué)院，四川 成都，610106)

邊坡穩(wěn)定性是巖土工程的重要研究?jī)?nèi)容之一，目前一般采用整體安全系數(shù)對(duì)邊坡穩(wěn)定性進(jìn)行評(píng)判[1-3]，這種方法無(wú)法反映邊坡各部位的安全狀況，因此，在邊坡支護(hù)過(guò)程中就需要進(jìn)行整體加固，從而造成浪費(fèi)。實(shí)際上，許多邊坡的失穩(wěn)往往是局部失穩(wěn)引發(fā)整體失穩(wěn)的，此時(shí)，若能夠加固這些危險(xiǎn)部位，則可防止邊坡的整體失穩(wěn)，因此，研究邊坡巖土體各部位的穩(wěn)定情況成為必要。一些學(xué)者也意識(shí)到這個(gè)問(wèn)題，并引入點(diǎn)安全系數(shù)或者屈服接近度的概念來(lái)評(píng)判巖土體各部位的安全狀況，如Hoek 等[4]最先將點(diǎn)安全系數(shù)引入到邊坡穩(wěn)定分析中。把點(diǎn)安全系數(shù)定義為巖土體中一點(diǎn)所能調(diào)動(dòng)的最大剪切強(qiáng)度與該點(diǎn)可能出現(xiàn)的剪應(yīng)力之比；沈可等[5]推導(dǎo)了基于Mohr-Coulomb 模型(MC 模型)的空間點(diǎn)安全系數(shù)公式；藍(lán)航[6]引入靜載強(qiáng)度分析研究了點(diǎn)安全系數(shù)計(jì)算方法；李樹(shù)忱等[7]根據(jù)彈性理論，利用MC 和Drucker- Prager 模型(DP 模型)，采用點(diǎn)安全系數(shù)建立了隧道圍巖穩(wěn)定評(píng)價(jià)指標(biāo)。張傳慶等[8-9]定義了Mohr-Coulomb 準(zhǔn)則下的屈服接近度指標(biāo)，并建立了屈服接近度求解函數(shù)，對(duì)圍巖中非塑性區(qū)的危險(xiǎn)程度進(jìn)行了定量研究。這些研究主要基于MC 或者DP 等線性模型，對(duì)巖體穩(wěn)定評(píng)價(jià)做出了有意義的貢獻(xiàn)，但巖體不同于金屬材料，其中廣泛分布著結(jié)構(gòu)面，導(dǎo)致其強(qiáng)度呈現(xiàn)非線性特征[10]，而線性模型無(wú)法反映該特征，存在一定局限性。因此，需開(kāi)發(fā)基于非線性模型的邊坡安全系數(shù)計(jì)算方法，一些學(xué)者基于Hoek-Brown 模型做了有意義的工作，如林杭等[11-12]擴(kuò)展了強(qiáng)度折減法在Hoek-Brown 準(zhǔn)則中的應(yīng)用；蔣青青[13]建立了Hoek-Brown 非線性模型下的邊坡穩(wěn)定性點(diǎn)安全系數(shù)。而對(duì)于節(jié)理巖體，普遍認(rèn)為JRC-JCS 模型(JJ 模型)能夠較好描述節(jié)理巖體特征[14-16]，若能建立該模型下的點(diǎn)安全系數(shù)計(jì)算方法對(duì)巖體邊坡各部位穩(wěn)定性進(jìn)行評(píng)判，具有一定工程和理論意義。基于以上考慮，本文作者首先推導(dǎo)了MC 模型下點(diǎn)安全系數(shù)的計(jì)算方法，然后，建立JJ 模型參數(shù)和MC 模型參數(shù)的關(guān)系，從而得到基于JJ 模型的非線性點(diǎn)安全系數(shù)計(jì)算公式。最后，研究JJ 模型參數(shù)對(duì)于點(diǎn)安全系數(shù)的影響，并通過(guò)算例分析，編制相應(yīng)的點(diǎn)安全系數(shù)程序，應(yīng)用于邊坡各部位巖土體的穩(wěn)定性分析中。

1 JRC-JCS 模型點(diǎn)安全系數(shù)

邊坡巖土體單元應(yīng)力的屈服(破壞)條件為：

式中：f 為應(yīng)力函數(shù)關(guān)系；σ 為應(yīng)力組合；H 為材料參數(shù)函數(shù)關(guān)系；κ 為材料參數(shù)的內(nèi)變量。

為了表征巖體單元的安全情況，引入安全系數(shù)的概念，其表達(dá)式為[13]：

通過(guò)計(jì)算得到相應(yīng)單元應(yīng)力值，以及材料參數(shù)值，并代入式(2)，即可得到點(diǎn)安全系數(shù)Fp。Fp能夠描述巖體單元的破壞程度，其受巖體參數(shù)、巖體內(nèi)應(yīng)力分布以及強(qiáng)度模型的影響。Fp＞1 表征巖體單元的應(yīng)力狀態(tài)未導(dǎo)致單元發(fā)生破壞，巖體處于穩(wěn)定狀態(tài)；Fp＜1表征的情況與Fp＞1 的情況相反；Fp=1 表征巖體處于臨界穩(wěn)定狀態(tài)。

為了在JJ 模型中建立相應(yīng)的點(diǎn)安全系數(shù)計(jì)算公式。取出單元的一個(gè)計(jì)算剖面，可得到該面上的剪應(yīng)力和剪切強(qiáng)度，當(dāng)剪應(yīng)力大于抗剪強(qiáng)度時(shí)，單元將沿該面發(fā)生剪切破壞。圖1 所示為巖體單元的Mohr 應(yīng)力圓，任一面上的應(yīng)力情況為

圖1 應(yīng)力Mohr 圓Fig.1 Stress Mohr circle

式中：σn為該面上的法向應(yīng)力；τ 為面上的剪切應(yīng)力；σ1，σ3為單元的最大和最小主應(yīng)力；α 為該面與最小主平面的夾角。

該面上的剪切強(qiáng)度τc為

式中：φ和c 分別為巖體的內(nèi)摩擦角和黏結(jié)力。

聯(lián)立式(2)～(5)，可得點(diǎn)安全系數(shù)的表達(dá)式：

從式(6)可知：點(diǎn)安全系數(shù)是關(guān)于α 角的函數(shù)，因此，為了得到Fp的最小值以確定巖體單元點(diǎn)的穩(wěn)定情況，對(duì)α 進(jìn)行求導(dǎo)。

將式(7)代入式(6)，即可確立Fp的計(jì)算公式：

從式(8)可以看出：MC 模型中，點(diǎn)安全系數(shù)主要取決于巖體的強(qiáng)度參數(shù)黏結(jié)力和內(nèi)摩擦角。因此，為了在JJ 模型中推廣點(diǎn)安全系數(shù)，只需確立JJ 模型參數(shù)與MC 準(zhǔn)則參數(shù)之間的關(guān)系，然后，將所確立的參數(shù)代入式(8)即可得到基于JJ 模型參數(shù)的點(diǎn)安全系數(shù)計(jì)算公式。

具體推導(dǎo)如下：

JJ 模型是巴頓通過(guò)大量節(jié)理巖體的剪切試驗(yàn)提出的[15]，其形式為

式中：τ 為巖體的剪切強(qiáng)度；σn為節(jié)理的正應(yīng)力；φb為巖體基本摩擦角，可取為30°的定值[16]；JRC為節(jié)理粗糙系數(shù)；JCS為巖體壓縮強(qiáng)度，低應(yīng)力條件下JCS對(duì)抗剪強(qiáng)度影響較小，隨法向應(yīng)力增大，JCS的影響亦增大。

對(duì)式(10)進(jìn)行三角關(guān)系變換，

從fa的計(jì)算公式中可以看出：當(dāng)σn→0 時(shí)，φb+JRC?lg(JCS/ σn)→∞，顯然這是不成立的。因此，Barton 等[15]建議： 在實(shí)際工程應(yīng)用中，φb+JRC?lgJCS/σn不應(yīng)該大于70°。法向應(yīng)力的極小值可用φb+JRC?lg(JCS/ σn)=70°反算得到，即，

對(duì)于邊坡巖土體，可參考Hoek 等[4]的建議得到法向應(yīng)力的最大值，

式中：γ 為巖體容重；H 為邊坡高度。

將式(9)～(11)代入式(6)即可得到JJ 模型的點(diǎn)安全系數(shù)Fp計(jì)算公式：

2 算例分析

2.1 JRC 和JCS 對(duì)Fp 的影響

取出邊坡巖體中某單元的應(yīng)力σ1=1.0 MPa，σ3=0.4 MPa，邊坡高為20 m，容重γ=26.0 kN/m3，分別改變材料參數(shù)JCS和JRC，分析各個(gè)參數(shù)對(duì)Fp的影響。假設(shè)巖體的基本摩擦角為30°，固定JCS=20 MPa，令JRC=0～20，得到圖2；固定JRC=6，令JCS=5～105 MPa，得到圖3。從圖2 和圖3 可以看出：隨著JRC和JCS的增大，巖體點(diǎn)安全系數(shù)Fp均呈現(xiàn)非線性增大，可通過(guò)指數(shù)方程對(duì)其關(guān)系進(jìn)行擬合，得到的相關(guān)系數(shù)分別為0.993 57 和0.997 72，屬于高度相關(guān)；Fp與JRC關(guān)系曲線的斜率隨JRC的增大而增大，而Fp與JCS關(guān)系曲線的斜率隨JCS的增大而減小。

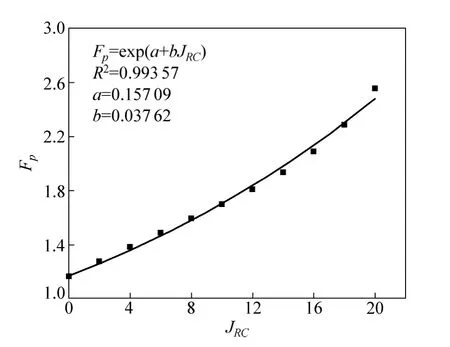
圖2 JRC 對(duì)Fp 的影響Fig.2 Effect of JRC to Fp

圖3 JCS 對(duì)Fp 的影響Fig.3 Effect of JCS to Fp

2.2 算例分析

某邊坡高20 m，建立節(jié)理概化模型，整體模型長(zhǎng)60 m，寬10 m，高40 m，單元數(shù)15 000，節(jié)點(diǎn)數(shù)17 391；邊界條件為：底部固定約束，四周約束法向位移，上部為自由邊界。初始應(yīng)力場(chǎng)按自重應(yīng)力考慮；計(jì)算收斂準(zhǔn)則為不平衡力比率(節(jié)點(diǎn)平均內(nèi)力與最大不平衡力的比值)滿足10-6的求解要求。計(jì)算參數(shù)為：彈性模量E=0.5 GPa，泊松比μ=0.28，容重γ=26.0 kN/m3。剪切模量G 和體積模量K 通過(guò)式(18)和(19)計(jì)算可得：

強(qiáng)度參數(shù)設(shè)置2 個(gè)方案：(1) φb=30°，JCS=20 MPa，JRC=2；(2) φb=30°，JCS=50 MPa，JRC=12。

數(shù)值計(jì)算過(guò)程中，根據(jù)彈性理論計(jì)算各個(gè)單元的應(yīng)變及應(yīng)力，然后，代入強(qiáng)度模型進(jìn)行判斷，若達(dá)到了屈服條件，則進(jìn)行相應(yīng)的應(yīng)力調(diào)整，使應(yīng)力滿足屈服函數(shù)，即使得單元體的應(yīng)力狀態(tài)回到應(yīng)力空間中的屈服面上，具體可參考文獻(xiàn)[17]。

通過(guò)差分法計(jì)算，根據(jù)式(17)利用FISH 語(yǔ)言編制相應(yīng)的點(diǎn)安全系數(shù)程序，得到的結(jié)果如圖4 所示。從圖4 可以看出：在靠近邊坡開(kāi)挖面位置，由于邊坡開(kāi)挖使圍巖約束消失，巖體存在向邊坡內(nèi)運(yùn)動(dòng)的趨勢(shì)，因此該部位的單元安全程度最低，部分區(qū)域的安全系數(shù)甚至小于1，由于FLAC3D 計(jì)算得到的塑性區(qū)表征的是安全系數(shù)小于1 的單元，因此將其與點(diǎn)安全系數(shù)公式計(jì)算得到的Fp≤1 的區(qū)域進(jìn)行對(duì)比，可以驗(yàn)證點(diǎn)安全系數(shù)公式的正確性，通過(guò)對(duì)比發(fā)現(xiàn)二者的分布范圍相同。另外，方案1 巖體的強(qiáng)度小于方案2 巖體的強(qiáng)度，引起邊坡各部位的安全系數(shù)小于方案2 的情況。

從本文的推導(dǎo)以及數(shù)值計(jì)算過(guò)程中可以看出：本文推導(dǎo)的關(guān)于JRC-JCS 模型下的點(diǎn)安全系數(shù)的計(jì)算公式，以及相應(yīng)的數(shù)值計(jì)算程序主要是針對(duì)均質(zhì)邊坡而言的，若邊坡中含有節(jié)理面或其他不連續(xù)面時(shí)，需考慮巖土體材料的非均勻性。

圖4 計(jì)算結(jié)果Fig.4 Calculation results

3 結(jié)論

(1) 推導(dǎo)得到了基于JRC-JCS 模型的非線性點(diǎn)安全系數(shù)計(jì)算公式。

(2) 在理論推導(dǎo)的基礎(chǔ)上，利用FISH 語(yǔ)言編制了計(jì)算程序，對(duì)比點(diǎn)安全系數(shù)Fp≤1 的區(qū)域與FLAC3D自身計(jì)算的塑性區(qū)分布范圍，二者基本一致，從而驗(yàn)證了自編程序的正確性，并且該程序結(jié)果能夠反映邊坡巖體各部位的穩(wěn)定情況。

[1] Griffiths D V, Lane P A. Slope stability analysis by finite elements[J]. Geotechnique, 1999, 49(3): 387-403.

[2] 趙尚毅, 鄭穎人, 鄧衛(wèi)東. 用有限元強(qiáng)度折減法進(jìn)行節(jié)理巖質(zhì)邊坡穩(wěn)定性分析[J]. 巖石力學(xué)與工程學(xué)報(bào), 2003, 22(2):254-260.ZHAO Shangyi, ZHENG Yingren, DENG Weidong. Stability analysis on jointed rock slope by strength reduction[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2):254-260.

[3] Dawson E M, Roth W H, Drescher A. Slope stability analysis by strength reduction[J]. Geotechnique, 1999, 49(6): 835-840.

[4] Hoek E, Bray J. Rock slope engineering[M]. London: Institute of Mineral and Metallurgy, 1981: 60-92.

[5] 沈可, 張仲卿. 三維抗滑穩(wěn)定分析中的點(diǎn)安全系數(shù)法[J]. 人民珠江, 2003(2): 21-22.SHEN Ke, ZHANG Zhongqing. Point safety factor method for 3-dimensional stability analysis[J]. Pearl River, 2003(2): 21-22.

[6] 藍(lán)航. 基于FLAC3D 的邊坡單元安全度分析及應(yīng)用[J]. 中國(guó)礦業(yè)大學(xué)學(xué)報(bào), 2008, 37(4): 570-574.LAN Hang. Analysis of zone safety degree of slopes and its application based on FLAC3D[J]. Journal of China University of Mining & Technology, 2008, 37(4): 570-574.

[7] 李樹(shù)忱, 李術(shù)才, 徐幫樹(shù). 隧道圍巖穩(wěn)定分析的最小安全系數(shù)法[J]. 巖土力學(xué), 2007, 28(3): 549-554.LI Shuchen, LI Shucai, XU Bangshu. Minimum safety factor method for stability analysis of surrounding rock mass of tunnel[J]. Rock and Soil Mechanics, 2007, 28(3): 549-554.

[8] 張傳慶, 周輝, 馮夏庭. 基于破壞接近度的巖土工程穩(wěn)定性評(píng)價(jià)[J]. 巖土力學(xué), 2007, 28(5): 888-894.ZHANG Chuanqing, ZHOU Hui, FENG Xiating. Stability assessment of rockmass engineering based on failure approach index[J]. Rock and Soil Mechanics, 2007, 28(5): 888-894.

[9] 張傳慶, 周輝, 馮夏庭, 等. 基于屈服接近度的圍巖安全性隨機(jī)分析[J]. 巖石力學(xué)與工程學(xué)報(bào), 2007, 26(2): 292-299.ZHANG Chuanqing, ZHOU Hui, FENG Xiating, et al.Stochastic analysis method on safety of surrounding rock mass based on yielding approach index[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(2): 292-299.

[10] Barton N, Pandey S K. Numerical modelling of two stoping methods in two Indian mines using degradation of c and mobilization of φ based on Q-parameters[J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 48(7):1095-1112.

[11] 林杭, 曹平, 趙延林, 等. 強(qiáng)度折減法在Hoek-Brown 準(zhǔn)則中的應(yīng)用[J]. 中南大學(xué)學(xué)報(bào)(自然科學(xué)版), 2007, 38(6):1219-1224.LIN Hang, CAO Ping, ZHAO Yanlin, et al. The application of strength reduction method in Hoek-Brown criterion[J]. Journal of Central South University (Science and Technology), 2007,38(6): 1219-1224.

[12] 林杭, 曹平, 李江騰, 等. 基于廣義Hoek-Brown 準(zhǔn)則的邊坡安全系數(shù)間接解法[J]. 煤炭學(xué)報(bào), 2008, 33(10): 1147-1151.LIN Hang, CAO Ping, LI Jiangteng, et al. The indirect calculation method for the safety factor of slope based on generalized Hoek-Brown criterion[J]. Journal of China Coal Society, 2008, 33(10): 1147-1151.

[13] 蔣青青. 基于Hoek-Brown 準(zhǔn)則點(diǎn)安全系數(shù)的邊坡穩(wěn)定性分析[J]. 中南大學(xué)學(xué)報(bào)(自然科學(xué)版), 2009, 40(3): 786-790.JIANG Qingqing. Stability of point safety factor of slope based on Hoek-Brown criterion[J]. Journal of Central South University(Science and Technology), 2009, 40(3): 786-790.

[14] 趙堅(jiān). 巖石節(jié)理剪切強(qiáng)度的JRC-JMC 新模型[J]. 巖石力學(xué)與工程學(xué)報(bào), 1998, 17(4): 349-357.ZHAO Jian. A new JRC-JMC shear strength criterion for rock joint[J]. Chinese Journal of Rock Mechanics and Engineering,1998, 17(4): 349-357.

[15] Barton N, Choubey V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics, 1977(10): 1-54.

[16] 杜時(shí)貴, 郭霄, 顏育仁. JRC-JCS 模型在抗剪強(qiáng)度參數(shù)取值中的應(yīng)用[J]. 金華職業(yè)技術(shù)學(xué)院學(xué)報(bào), 2004, 4(1): 1-4.DU Shigui, GUO Xiao, YAN Yuren. JRC-JCS model and its application on studying shear strength of rock joint[J]. Journal of Jinhua College of Profession and Technology, 2004, 4(1): 1-4.

[17] Itasca Consulting Group. User’s Guid[M]. Minnesota: Itasce Consulting Group, 2002: 152-156.