基于集對分析的石膏礦采空區穩定性評價
肖 超,鄭懷昌,武文治,褚召偉,王 棟,張曉君
(1.山東理工大學資源與環境工程學院,山東 淄博 255049;2.棗莊嶧城區建材局,山東 棗莊 277000)
石膏礦山多數運用房柱法開采,不可避免遺留了大量采空區,并且采空區大多未得到處理,因此正確評判礦山采空區穩定性,為后期處理采空區提供依據﹑對礦山安全生產具有重要意義。目前評判采空區穩定性方法眾多,早期砌體梁結構和關鍵層理論用來分析支撐采空區結構穩定性的體系,模糊數學﹑灰色理論和神經網絡等非線性方法在預測采空區塌陷問題實際應用中取得了較好的效果,鄭懷昌等[1]利用界殼理論對采空區失穩判定進行了探討;吳啟紅等[2]建立了礦山采空區穩定性的二級模糊綜合評判模型;張耀平等[3]利用 FLAC3D對采空區形成過程及穩定性進行了模擬計算;張曉君[4]基于可靠度對采空區的穩定性進行了分析;文獻[5]基于突變級數理論,分析影響采空區穩定性的因素;宮鳳強等[6]基于未確定測度理論,建立礦山采空區的危險性等級評價和排序模型;唐碩等[7]構建采空區穩定性模糊物元評價模型,用關聯度表示評價結果;李明等[8]總結了影響石膏礦山采空區整體穩定性的主要因素并采用數值模擬軟件FLAC3D對關鍵因素進行了驗證分析;廖文景等[9]對影響礦柱及護頂層穩定性的各因子進行了敏感性分析;鄭茂興等[10]提出了采空區穩定性分類的綜合評判法;肖超等[11]運用層次分析法對采場穩定性進行評價并利用FLAC3D進行驗證。
然而采空區穩定性是一個包含采空區本身和周圍地質構造及所覆巖層巖性性質同時又受到開采和爆破造成的擾動﹑地下水﹑時間引起的流變等復雜多因素影響的大尺度平衡問題[12],影響采空區穩定性的因素較多,有著確定﹑不確定的耦合關系,已往評價方法大多只選取少數代表性的評價指標和部分信息,或者利用簡單的線性表述,難以采集到影響采空區穩定性因素的全部信息,難以全面、準確反映現場地質概況,其評價結果具有很大的局限性;雖然近年來采用模糊數學方法、模糊可變集合、人工神經網絡方法等方法能較全面顧及到各個因素,但模糊綜合評判中的“最大隸屬原則”對信息篩選的全面性有待斟酌。
集對分析是一種處理不確定性問題的系統分析方法,核心就是把不確定性與確定性作為一個系統加以處理,本文結合影響石膏礦采空區穩定性13個評價指標評判情況,利用集對分析理論來評價石膏礦采空區穩定性。
1 石膏礦采空區穩定性影響指標選擇及判別
本文選取采空區幾何參數(礦柱寬高比﹑礦柱面積比率﹑礦房跨度超標程度﹑護頂層﹑ 上部膏層隔離礦柱)﹑地質因素(巖體結構﹑構造)﹑外界環境因素(采深﹑采動﹑地下水﹑采空區存在時間)三方面13個影響因素進行分析。
1.1 采空區幾何參數
1)礦柱寬高比k1直接制約采場穩定性。通常而言,當寬高比大于2~4倍時不易發生大面積冒頂,這種礦柱往往可起到防止頂板冒落的隔離保護作用[13]。
2)礦柱面積比率k2是殘留礦柱面積與采空區總面積之比,礦柱和礦房頂板兩個基本要素共同決定以空場采礦法為背景的采空區穩定性狀態。建立礦柱面積比率k2函數見式(1)。
(1)
式中:a和A分別為礦柱和礦房的寬度,m。
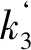
(2)
4)房間柱破壞程度k4。在空場采礦法中為了保證礦房頂板在開采礦房期間不會由于暴露面積過大而垮落,通常設置房間礦柱,相當于支撐頂板的簡支梁。設礦柱原來留設的斷面面積為S′,空區形成一段時間后房間柱的斷面面積為S,則有關于房間柱破壞程度k4的函數見式(3)。
(3)
5)護頂層k5。由于石膏礦山上覆巖層大多為泥巖或砂質泥巖,通常在采場中留一定厚度石膏層來防止頂板冒落﹑維護頂板穩定性。在薄頂板層中,重力荷載和張開造成撓曲與側向力,于是產生了在它們的作用下頂板巖層的穩定問題[14]。
設σT﹑τ為護頂層所受拉應力和所受剪應力,σT﹑τ分別為石膏護頂層的抗拉強度和抗剪強度,則有石膏護頂層k5函數,見式(4)。
(4)
6)上部膏層k6。上部膏層即為采空區頂板上方幾米處留下的一條石膏層,作用是使得處于下部的護頂層只承受來自其上軟弱巖層的重量,從而維護采場穩定性。
建立關于上部膏層指標k6的函數見式(5)。
(5)
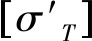
7) 隔離礦柱k7。采空區從形成到崩塌根源是應力轉移與集中﹑圍巖與內部礦柱支撐能力下降,建立隔離礦柱指標k7分段函數見式(6)。
(6)
式中:L隔柱為隔離礦柱間距,m;B為礦房的極限跨度,m。
1.2 地質因素
1)結構k8。巖體結構決定著巖體工程地質特征,是由結構面和結構體兩個要素構成,起到影響巖體的物理力學性質﹑內在特性及其受力變形的作用。
按照式(7)計算巖體質量指標法中指標Q的數值。
(7)
式中:RQD為Deere巖石質量指標;Jn、Jr、Ja、Jw分別為節理組數﹑粗糙程度系數﹑壁蝕系數﹑水折減系數;RF為應力折減系數。
巖石結構指標k8的函數見式(8)。
k8=RQD
(8)
2) 構造k9。沖擊地壓的臨界開采深度受到構造應力的影響明顯減小,處于復雜的地質構造中的采空區的安全穩定性差﹑危險度高,建立構造指標k9的分段函數見式(9)。
(9)
式中:r′為構造距離空區中心的距離,m; A為礦房的實際跨度,m;
1.3 外界環境因素
1) 采深k10。隨著開采進行,采深不斷增大,巖體逐漸發生移動﹑地表有塌陷現象,最終可能造成大面積巖體移動并導致地表破壞,建立采深指標k10的分段函數,見式(10)。
(10)
2)地下水k11。影響巖體質量的另一個重要因素是地下水,地下水弱化巖石強度﹑影響著各種結構面的阻抗能力大小,建立地下水指標k11的分段函數,見式(11)、式(12)。
普通石膏
(11)
硬石膏
(12)
式中:Rc濕和Rc干分別為濕石膏試件和干石膏試件的抗壓強度;Rt濕和Rt干分別為濕石膏試件和干石膏試件的抗拉強度。
3) 采動k12。不斷開采爆破過程中,采場圍巖應力重新分布﹑“礦柱-頂板-底板”抗塌性體系抗塌能力不斷下降,建立采動指標k12的分段函數,見式(13)。
(13)
式中:r為采動影響因素距離最近空區邊界的距離,m;A為礦房實際跨度,m。
4) 采空區存在時間k13。伴隨時間的延續,空區面積不斷增大,一方面,承載礦柱的能力在下降;另一方面,由于部分礦柱提前失穩,應力轉移到相鄰礦柱,建立采空區存在時間指標k13的函數,見式(14)。
(14)
式中:t為采空區存在時間,a(年);T為統計顯示的空區存在但不垮落的平均時間,a(年)。
采空區穩定性分為很差(Ⅰ)﹑較差(Ⅱ)﹑一般(Ⅲ)﹑較好(Ⅳ)四個穩定性等級,見表1。

表1 指標評分值
3 石膏礦采空區穩定性集對分析模型
3.1 原理
集對分析作為一種用來處理不確定性模糊耦合問題的系統分析方法,是由我國學者趙克勤提出,關鍵是處理不確定性與確定性這一系統,即一定條件下,以同一性、差異性、對立性的系統來分析組成集對的兩個集合特性,同時通過聯系度μ定量描述。
3.2 聯系度
設集合Aj=(x1,x2,x3,x4,…,xN)(j=1,2,…n)和集合Bk=(y1,y2,…,yN)(k=1,2,3,4)組成集對H=(Aj,Bk)做分析,共獲得N個特性,A、B所共有S個特性,特性對立的有P個,剩下的F=N-S-P相異,則有式(15)。
(15)

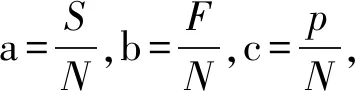
μ=a+bi+cj
(16)
式中:i為差異度系數,i∈-1,1,取值不確定;j為對立系數,j=-1。
同、異、反三者的關聯性是通過聯系度表達式來體現的,當i等于1時,不確定度轉化成同一度,當i等于-1時,則不確定度轉化成對立度;當i處于-1和1之間時,展現了確定性與不確定性所擁有的比例。
3.3 集對分析模型
由上文知采空區危險性劃分四個等級,設集合Aj=(x1,x2,x3,x4,…,xN)(j=1,2,…n)為影響采場穩定性的指標樣本實測值,集合Bk=(y1,y2,…,yN)(k=1,2,3,4)為四個等級下各指標標準,構建集對H=(Aj,Bk)。 “同”是測得的樣本各指標值歸為相應等級;“異”包括相差一級和兩級,其中相差一級的,如Ⅰ和Ⅱ,Ⅱ和Ⅲ,Ⅲ和Ⅳ,為差異一,其個數計為F1;相差兩級的,如Ⅰ和Ⅲ,Ⅱ和Ⅳ,為差異二,其個數計為F2;“反”是相隔三級,如Ⅰ和Ⅳ。得到聯系度,見式(17)。
(17)
評價采空區穩定性時,參照相關資料取i1=0.5,i2=0.25。μ(Aj,Bk)越大表示樣本與某等級的同一性越高[15]。
4 工程實例
4.1 石膏礦采空區穩定性影響指標計算
本文選取棗莊嶧城區一石膏礦進行采空區穩定性評價,本石膏礦房間柱有礦柱,無破壞,無變形;上部膏層厚1.5m,基本完整,巖體結構屬層狀結構:區內基本無斷層,褶皺構造不發育,在采空區內盤區間隔離礦柱無破壞、無變形,井田隔離礦柱完好,本礦的采空區平均采深在175m左右,井下無水,空區有少量積水,該礦為一次采動,主要大空區的存在時間為10年。表2為實測指標評分值。
4.2 采空區穩定性集對分析模型評價
表3為采空區穩定性評價結果。

表2 實測指標評分值

表3 采空區穩定性評價結果
由于u(Aj,B3)最大,故評價結果為Ⅲ級。
5 結論
1)采空區穩定性影響因素眾多,很多因素所起作用大小不盡相同,且微小因素也不能忽略,以往評價采空區穩定性只是簡單選取幾個主要因素,本文選取13個因素,幾乎涉及到采空區穩定性影響因素各個方面,并對這些因素指標進行了評判。
2)相比以往指標評價法進行計算時很多指數都是硬性施加,本文利用集對分析理論,通過探討樣本值與標準值之間的聯系度,構建集對分析模型,很好得解決了石膏礦采空區穩定性這一系統問題,計算簡單﹑實用,具有較廣應用價值。
[1] 鄭懷昌,李明.界殼理論在采空區失穩判定與危害控制研究中的應用探討[J].黃金,2005,26(12):19-22.
[2] 吳啟紅,彭振斌,陳科平,等.礦山采空區穩定性二級模糊綜合評判[J].中南大學學報:自然科學版,2010,41(2):661-667.
[3] 張耀平,曹平,袁海平,等.復雜采空區穩定性數值模擬分析[J].采礦與安全工程學報,2010,27(2):233-238.
[4] 張曉君.影響采空區穩定性的因素敏感性分析[J].礦業研究與開發,2006,26(1):14-16.
[5] 陳紅江,李夕兵,高科.突變級數法在采空區塌陷預測中的應用[J].安全與環境學報,2008,8(6):108-111.
[6] 宮鳳強,李夕兵,董隴軍,等.基于未確知測度理論的采空區危險性評價研究[J].巖石力學與工程學報,2008,27(2):323-330.
[7] 唐碩,羅周全,徐海.基于模糊物元的采空區穩定性評價研究[J].中國安全科學學報,2012,22(007):24-30.
[8] 李明,劉志河,苗強,等.采空區穩定性主要影響因素分析[J].化工礦物與加工,2013,9:20-24.
[9] 廖文景,徐必根,唐紹輝.石膏礦采空區穩定性主要影響因素正交試驗研究[J].礦業研究與開發,2011,(6):14-17,25.
[10] 鄭茂興,陳明磊,楊久富,等.石膏礦采空區穩定性分類的綜合評判法研究[J].化工礦物與加工,2012,41(5):24-27.
[11] 肖超,鄭懷昌,王棟,等.基于層次分析法采場穩定性評價及FLAC3D模擬驗證[J].山東理工大學學報:自然科學版,2014,28(1):65-68.
[12] 肖超,鄭懷昌,王棟,等.石膏礦采空區穩定性研究進展[J].山東理工大學學報:自然科學版,2013,27(5):36-39.
[13] 王官寶.石膏礦冒頂引發沖擊地壓機理及防治措施研究 [D].武漢:武漢理工大學,2006.
[14] 徐必根,黃英華,劉小林.護頂層對石膏礦采空區穩定性影響研究[J].礦業研究與開發,2007,27(5):20-22.
[15] 吳大國,汪明武,張薇薇.基于集對分析的圍巖穩定性評價[J].西部探礦工程,2008,20(2):6-7.

