煤礦礦建工程投資估算模型與應用
張召冉,楊仁樹,許 炳,牛天勇
(1.北方工業大學經濟管理學院,北京 100141;2.中國礦業大學(北京)力學與建筑工程學院,北京 100083)
煤礦建設項目具有結構復雜、規模大、工期長,同時工程造價具有投資額大的特點,對于現代化礦井動輒十幾億的投資,工程投資估算的確定及控制對業主來講意義重大[1]。投資估算是決策階段重要的參考指標之一,是投資控制的第一步,也是建設項目投資的最高限額[1],估算準確與否直接關系到項目后續投資控制的難易程度。
造價估算的方法主要有3種。一種是指數估算法[1],如單位面積綜合指標估算法,生產規模指數估算法,單元指標估算法等方法。另一種是回歸模型和模糊類比模型。這些方法準確度不高、誤差不穩定,外推性差,在高度不確定性和非線性條件下具有局限性,尤其是在條件復雜的礦建工程方面不適合[2]。第三種是人工神經網絡方法,這種方法正好能彌補其他兩種傳算造價方法的缺點,在預測和評價方面的準確性明顯高于回歸模型和其他的方法[3-4]。
人工神經網絡具有很強的非線性映射能力,所以在工程領域應用比較廣泛,如:橋梁工程投資估算模型[5];住宅工程神經網絡投資估算模型[6-7];隧道工程投資估算預測[8];路基工程投資估算模型[9]。人工神經網絡尤其是BPNN在土建工程方面應用較成熟,但是在礦建工程方面研究不多。王有良等利用BP神經網絡對煤礦企業可持續發展進行預測[10-12];邵良杉等在分析工程造價估算模型的發展的前提下提出利用神經網絡進行煤礦井巷工程的估算[13],該模型預測指標過多,數據處理不徹底。本文在前人研究的基礎上,在分析礦建工程投資估算構成分解的基礎上建立礦建投資模型,應用BPNN對礦建工程投資估算額進行預測。
1 礦建工程投資估算模型的建立
在礦建工程中,按照生產環節可以劃分為施工準備工程、井筒、主要運輸道及回風道、井底車場巷道及硐室、采區、排水系統和供電系統7部分,它們構成了礦建工程投資的主體。各個部分對工程投資影響因素不同,因此需將整個礦建工程投資分為若干組成部分,先分別建立各個部分投資估算子模型,當需要對某一項進行估算時,就選用與之相匹配的子模型即可進行估算。
通過對礦建工程項目分解,煤礦礦建工程投資估算可以細分為分為立井井筒、斜井井筒、井底平巷、(上山、下山)巷道、交岔點、硐室、工作面開切眼、煤倉、排水、供電10個估算模型[2],通過神經網絡的學習能力,可分別對各個部分進行造價估算的計算。各估算子模型組成估算模型系統(圖1),從而實現對礦建工程造價的整體估算。本文僅以井底平巷造價估算為例,探討煤礦礦建工程投資的神經網絡估算方法。
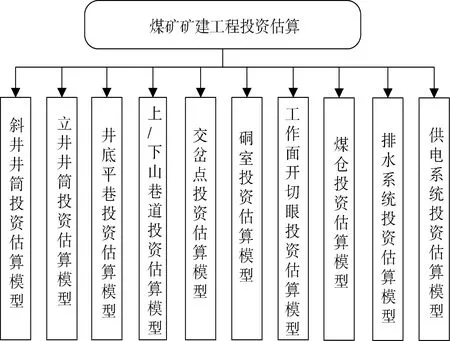
圖1 礦建工程投資構成系統
2 工程特征的選取
工程特征是某一類工程所具有的特點,能夠準確的描述工程主要構成成本情況[6-7,14],其又可以分為技術特征和經濟特征。經濟特征與造價直接相關,如鋼筋網消耗量;而技術特征與造價間接相關,如支護方式及參數。所以工程特征的選取是建模過程中的關鍵一步,對估算結果的精確度影響較大,工程特征選取越準確,越能準確體現造價信息。充分考慮巷道工程的特點,通過對所搜集到的工程量清單和相關數據的分析以及對專家的咨詢,選取以下特征為平巷的工程特征。
1)圍巖類別。對巷道施工來講,圍巖類別決定了施工的難易程度,也決定了采取的支護設計和施工方法,其對巖巷掘進的速度產生重大影響。我國的煤炭部門把圍巖分為五類:穩定、基本穩定、穩定性差、不穩定、極不穩定。
2)斷面大小。對單位巷道來說,斷面大小就是巷道掘進工作量,而掘進工作量是計算工程造價的重要指標,本文所指斷面是指設計斷面。
3)支護方式。巷道支護是對井巷、硐室所采取的保護措施。支護方式決定了支護所需要的支護材料消耗量,所使用人工和機械消耗量,從而影響著工程造價。
4)支護厚度。單位巷道內支護厚度決定了支護材料(砂石、水泥、)的消耗量。
5)錨桿消耗量。即單位長度內錨桿的消耗量,與工程投資密切相關。用錨桿密度(根/m)與相應規格錨桿的體積的乘積來表示。
6)鋼筋消耗量(kg/m)。鋼筋網是巷道工程重要的支護材料,是組成工程投資的重要部分。
7)錨索和支架消耗量。遇有不穩定圍巖或地壓很大的情況下,要采用聯合支護的形式來保證巷道的安全,其消耗量對工程造價影響較大。錨索消耗量用密度與錨索規格來表示,由于采用的規格均為φ15.24mm×6m可不予考慮,所以單位為根/m。支架均采用29U鋼支架,單位為t/m。
3 BP人工神經網絡模型
3.1 人工神經網絡簡介
人工神經網絡(Artificial Neural Network)是20世紀80年代后期發展起來的新學科。它具有自我學習、自我適應和處理非線性動態問題的能力。人工神經網絡可以保存綜合評價過程中每個指標的權重,建立一個綜合評價選擇模型,這個過程對人類思維模式的定性接近和定量模仿[6]。
3.2 BP神經網絡模型的建立
誤差反傳前饋網絡(Back Propagation)是目前被廣泛應用且發展比較成熟的神經網絡[8],它是典型的前饋網絡,是一種具有三層或三層以上的神經網絡,具有簡單處理功能的神經元的復合作用,使網絡具有非線性映射能力。典型的BP神經網絡見圖2。投資預測巷道子模型模型參數的選擇如下所示。
1)選擇網絡隱含層個數。根據文獻研究,在任意給定的精度上3 層神經網絡已經滿足所有要求;隱含層多,網絡結構就大,所以學習和訓練時間就長。根據以上原理,本文的神經網絡模型采用3層,隱含層設定為1層,按Kolmogorov定理,取值為2n+1(n為輸入向量的個數)。
2)初始權值確定。通常情況下,初始值采用隨機函數(-1,1)之間的隨機數在機上隨機選取。
3)節點函數選取。一般BPNN的節點采用sigmoid函數作為節點函數,隱含層傳遞函數采用“S”型tansig,輸出層傳遞函數采用logsig,這樣任何輸入數據都可以轉化成為(0,+1)之間的數。
4)盡管BP算法具有理論上的完善性和廣泛的實用性,但其收斂速度慢,會出現局部極小點問題,且網絡學習、記憶性差。因此本文采用改進后的BP算法(圖2)。
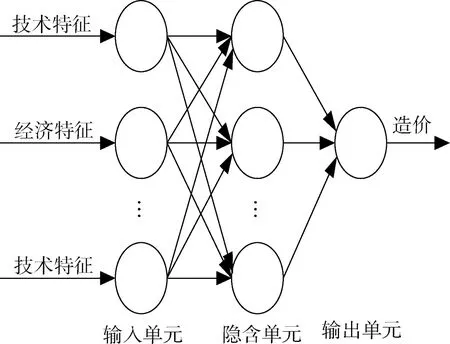
圖2 BP神經網絡結構
學習速率η也稱為步長,在標準的BP算法中是常數,其選擇范圍在0.01~0.8之間 。但在實際應用中,很難確定一個自始至終合適的最佳學習速率,選的過大會使訓練的過程引起震蕩,選的過小會使訓練的過程更加緩慢。為解決這個問題,人們根據學習進展情況(一般指訓練誤差)在訓練過程中改變學習速率。有很多方法可以改變學習速率,它們的目的都是使得在整個訓練過程中保證算法的收斂性。下面給出一個自適應學習速率的調整公式。
η(k+1)=
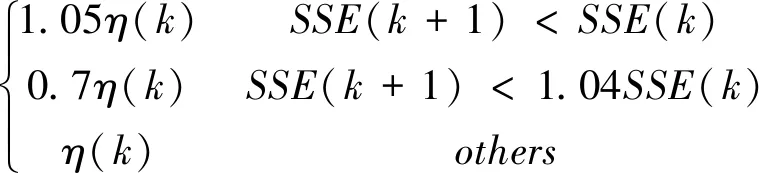
初始學習速率η(0)的選擇范圍有一定的隨意性。通過利用歷史統計資料,神經網絡模型可以建立類似問題的良好預測。但如果追求足夠小的學習誤差,往往導致“過度訓練”現象,也就是說,隨著學習誤差的下降,網絡的預測能力逐步提高,但是,當學習誤差下降到最小值時,網絡的預測能力反而更差。為避免出現過度訓練,在神經網絡模型的研究中,我們可以通過預先的大量研究,找出合理的、令人滿意的學習次數。
4 巷道造價估算的神經網絡模型建立及應用
巷道估算值可以采用式(1)進行計算。
巷道造價估算值(V)=巷道長度(L)×每米造價(O)
(1)
所以本文僅以巷道每米造價為預測值,為了更好的說明估算模型的計算過程,本文選取同一煤礦14個井底平巷的數據為樣本,數據見表1(因為收集的樣本為二類圍巖,為簡化計算,所以本例刪除圍巖類別這個輸入單元。)
通過表1可以看出,工程特征之間的描述和量綱不同,有的是工程特征是文字類,有的是數值類的,文字型向量在Matlab中無法識別,需對其進行量化,所以將支護形式和圍巖類別分別賦予不同的值(此數值沒有實際意義,只起到區分作用),作為文字型輸入變量的值,對支護形式和圍巖類別的賦值見表2。賦值整理后的樣本如表3所示。
通過表3可以看出,輸入向量之間的數量級差別很大,為了使運算簡便,防止出現神經元過飽和現象,加快神經網絡收斂速度,將斷面大小、支護形式、支護厚度、錨桿消耗量、鋼筋消耗量、錨索和支架消耗量、每米造價8個指標,通過式(2)對數據進行歸一化處理,將每個值都化為0~1之間的值;對于最終造價預測結果,采用式(2)的反歸一化公式(3)。
(2)
(3)
以樣本中前12個數據為學習樣本,后2個數據為訓練樣本。基于標準化的數據,建立包含一個隱含層的三層BP網絡模型,用7個指標作為輸入單元(I),1個指標(每米造價O)輸出單元。
本文采用Matlab提供的BP網絡函數構建模型。設置訓練精度設計值為10-10。先對12組樣本數據進行網絡訓練,網絡訓練22次就建立了輸入指標與造價的映射關系,達到精度要求,即收斂后的網絡(圖3)可以對第13組、14組數據的單位造價進行預測。預測過程中,難免有誤差的存在,所以單次預測準確性不高,為提高預測的準確性,運行20次[14],求均值將其作為O預測值,見表4。
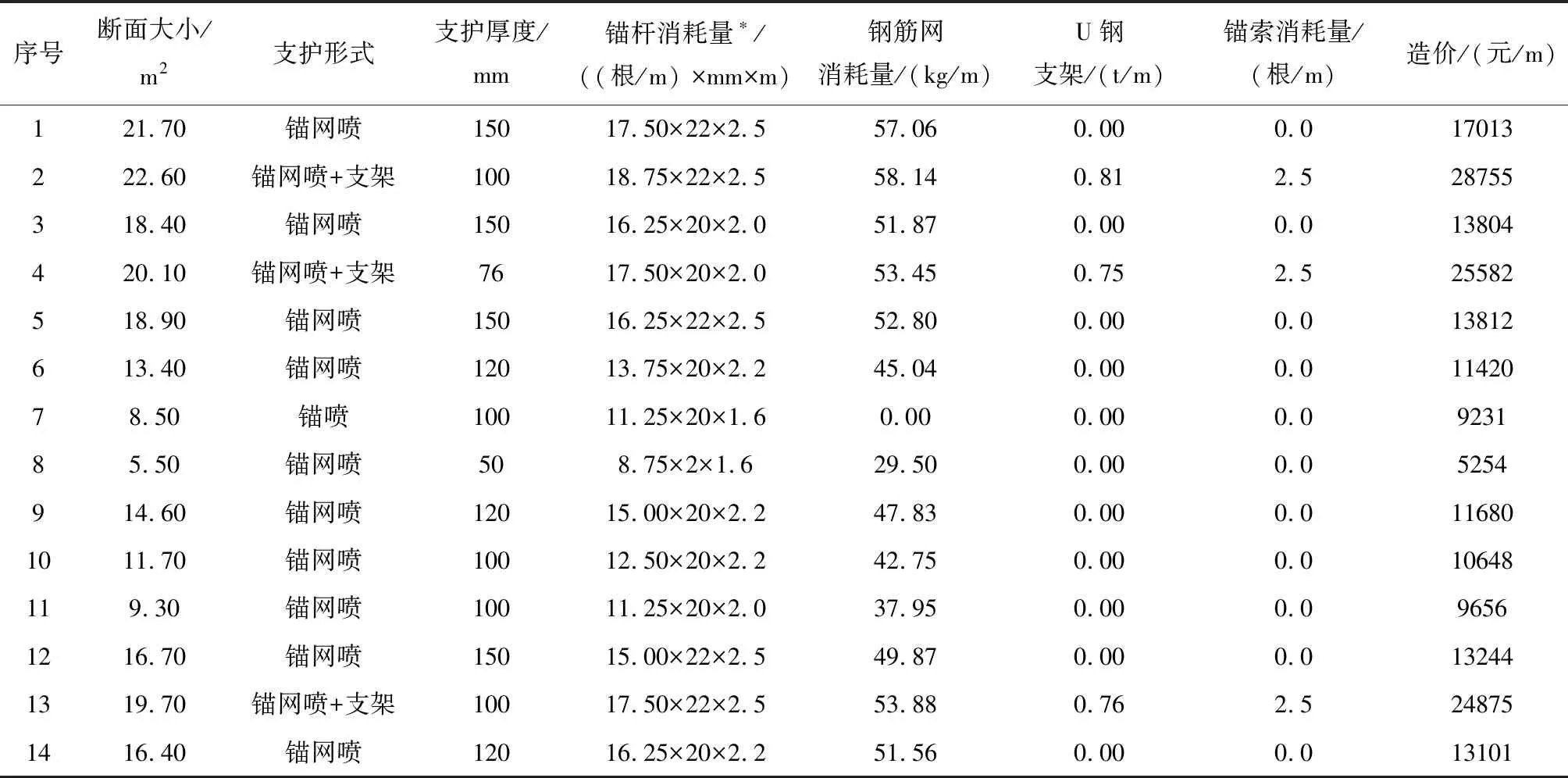
表1 巷道樣本數據統計列表
注:*為便于表達此處錨桿消耗量用錨桿密度與錨桿直徑和錨桿長度的乘積表示。

表2 支護形式賦值表

表3 圍巖類別賦值表
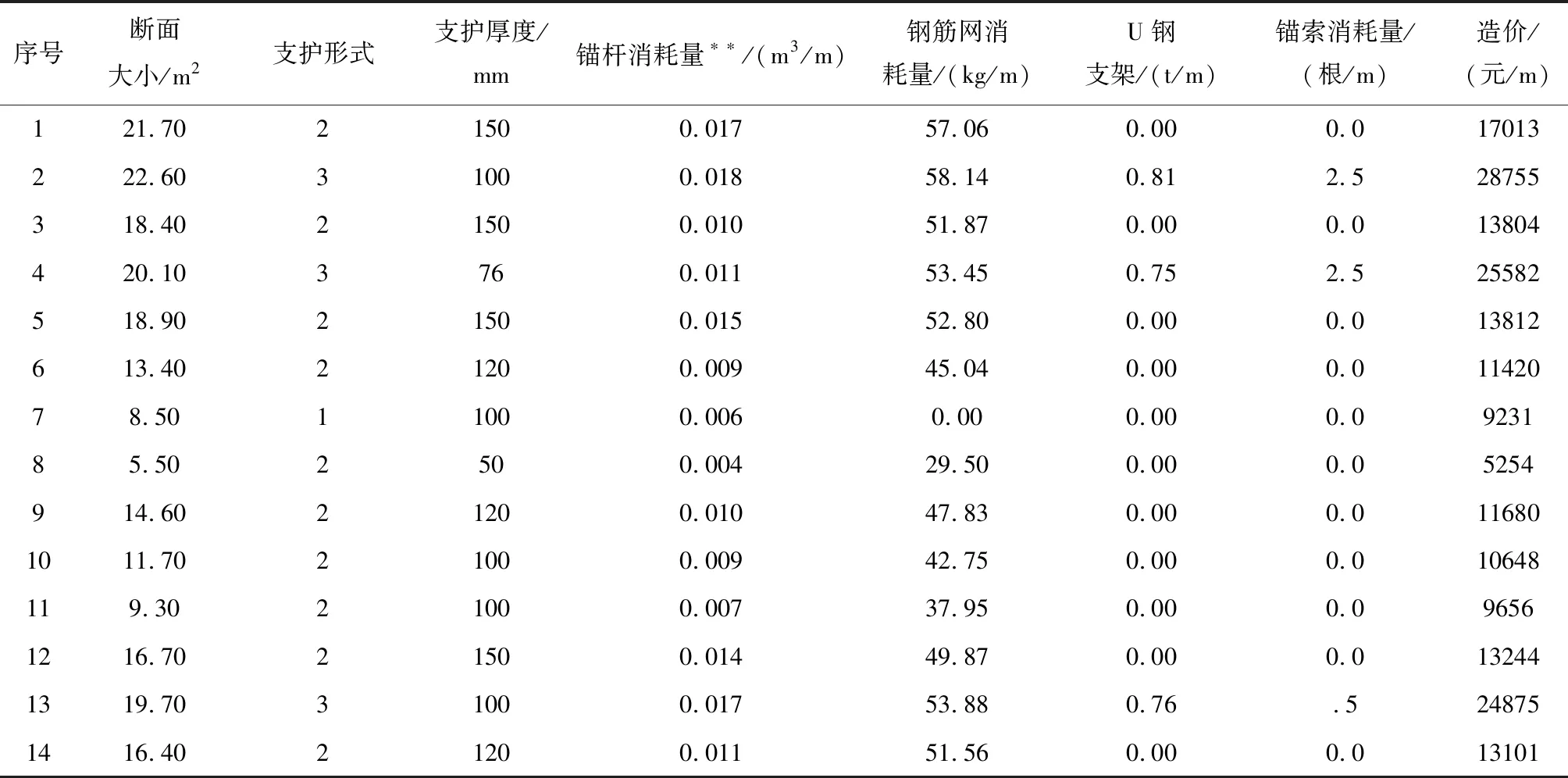
表4 巷道樣本數據賦值統計列表
注:**此處錨桿消耗量用錨桿密度與錨桿體積的乘積表示,即每米巷道錨桿總體積。
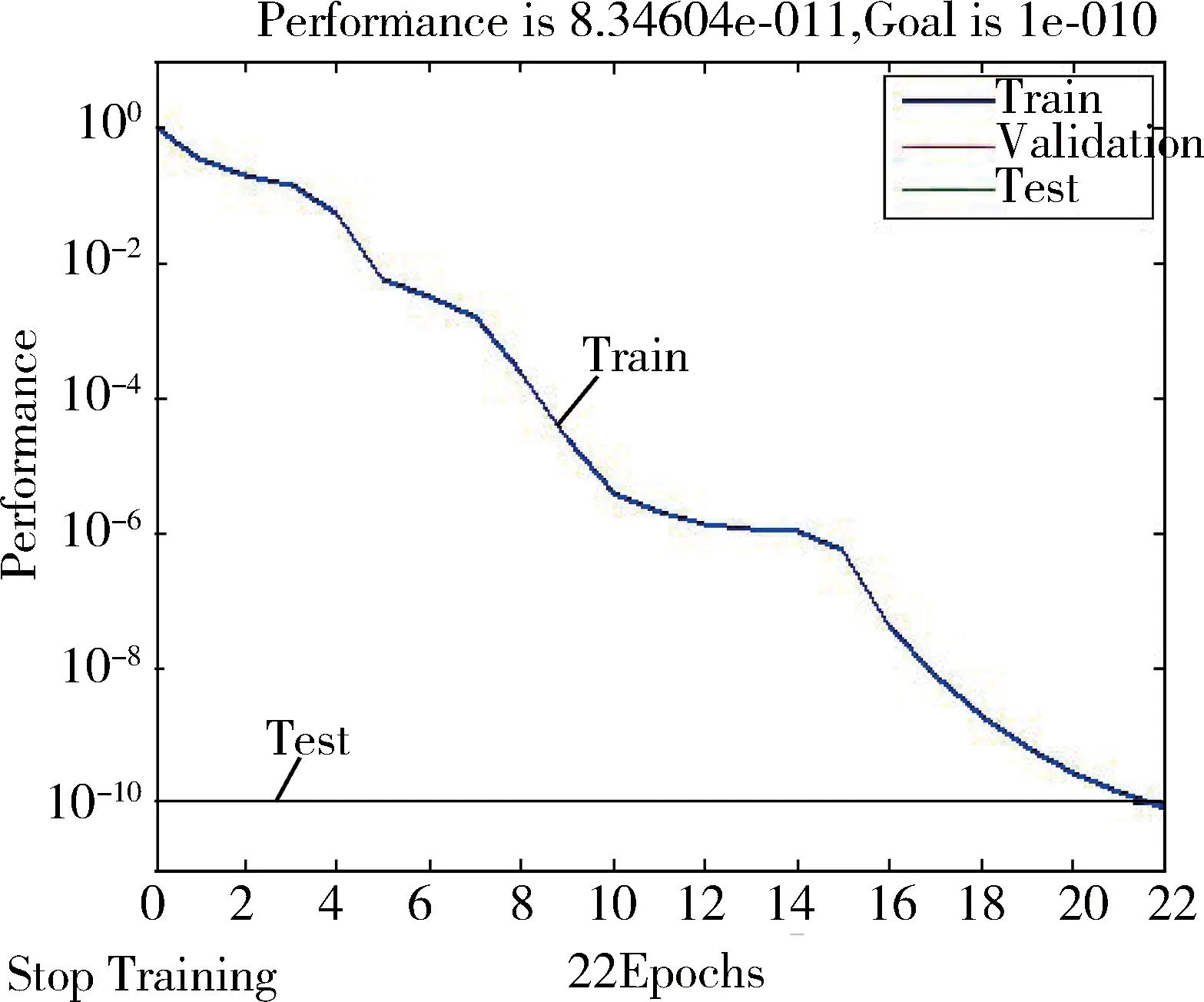
圖3 網絡收斂過程
表5 BP網絡運行結果
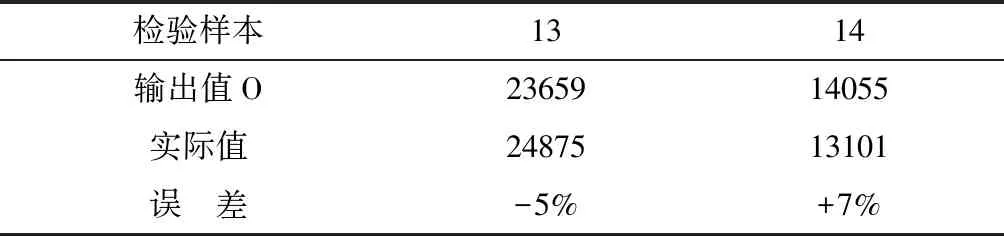
檢驗樣本1314輸出值O2365914055實際值2487513101誤 差-5%+7%
5 結果分析
運用MATLAB對編寫程序進行的預測值并平均后與實際值進行比較,從表5可見,求均值之后的預測值與實際值相對誤差很小,完全能夠滿足估算精度要求(≤±10%)。從單次神經網絡運行結果來看,有些預測的誤差較大,但是通過多次運行網絡后求均值,就可以保證較高預測精確度。
6 結論
1)BPNN模型的建立主要取決于工程特征的選取和訓練樣本的選取兩個方面,只要工程特征和樣本選用合理,同時BP網絡模型參數選用準確,預測結果就能達到估算精度±10%的要求。
2)盡管構建的BP網絡每次給出的預測各不相同,具有一定隨機性。但多次運算之后,通過求均值可以極大消除這種隨機性。
3)BPNN模型的容錯性對于不確定性因素較多的礦建工程的投資估算具有一定優勢,擯棄了復雜數學模型,精度高且節省大量時間,在復雜的礦建工程領域具有廣闊應用前景。
[1] 吳立之.工程投資估算的新方法[D].大連:大連理工大學,2003.
[2] 溫國鋒.基于人工神經網絡的煤炭建設項目投資估算系統的研究[J].中國煤炭,2002(7):12-14.
[3] 邵良杉,高樹林. 基于人工神經網絡的投資預測[J].系統工程理論與實踐,1997(2):68-72.
[4] 邵良杉,高樹林.工程造價人工神經網絡估算系統[J].煤礦設計,1996(4):43-46.
[5] 汪安南,王九大.基于人工神經網絡的建設項目投資估算模型[J].治淮,2006(6):17-19.
[6] 葉青,王全鳳.基于BP神經網絡的工程估價模型及其應用[J].廈門大學學報:自然科學版,2008(6):828-831.
[7] 周麗萍,胡振鋒.BP神經網絡在建筑工程估價中的應用[J].西安建筑科技大學學報:自然科學版,2005(2):262-264.
[8] 余建星,段曉晨,張建龍.基于BP神經網絡數據挖掘方法的政府投資項目投資估算方法[J].中國農機化,2006(5):36-39.
[9] 王運霞,劉志強,黃成.基于BP神經網絡的路基工程投資估算模型[J].中外公路,2008(2):66-68.
[10] 王有良,唐躍剛.煤礦企業可持續發展BP神經網絡預測[J].山東農業大學學報:自然科學版,2009(3):416-420.
[11] 徐君,杜文,曾旗.基于BP神經網絡的煤炭企業可持續發展評價[J].西南交通大學學報,2005(3):375-378.
[12] 王永保,吳玉萍.基于BP神經網絡的煤炭企業可持續發展評價[J].遼寧工程技術大學學報,2007(5):769-772.
[13] 邵良杉,楊善元.工程造價估算模型的發展及神經網絡估算模型[J].煤炭學報,1996(2):134-138.
[14] 段曉晨.政府投資項目全面投資控制理論和方法研究[D].天津:天津大學,2006.

