架空線抗彎剛度及其計算方法探析

陳 亦 祝益民

（1.廣東電網有限責任公司江門供電局，廣東 江門529000；2.浙江雷鳥智能電網技術有限公司，浙江 杭州311121）

0 引言

輸電線路在線監測的一個重要功能是對導線的微風振動進行監測，即通過直接測量懸垂線夾附近的彎曲振幅［1］（線夾出口89 mm處的彎曲振幅），計算得到線夾出口動彎應變的大小，并在此基礎上對線路的微風振動狀況及導線預期壽命進行評估。

1 抗彎剛度的概念

材料力學中的抗彎剛度指的是物體抵抗其彎曲變形的能力。對于大部分結構簡單、變形單一的構件來說，只要求出了慣性矩，一切都變得非常簡單。但是，對于像架空線這樣結構復雜、具有組合變形特點的構件來說，抗彎剛度的真實值的識別又變得異常復雜。

2 架空線抗彎剛度的特點

許多實踐證明，除了結構本身因素外［2］，影響索結構的抗彎剛度的最重要因素是作用于索結構上的張力T，其相關度r可達0.999 2，且抗彎剛度與張力T之間存在很好的線性關系。架空線導線張力對抗彎剛度的影響主要以兩種形式出現：（1）當架空線不受力（張力為0）時，絞線截面的慣性矩就是各根鋁線和鋼絲的慣性矩的代數和；而在實際工程中，當絞線承受了一定的張力時，各單線之間的粘結作用不可忽略，此時需要考慮架空線的整體作用。（2）當架空線承受張力時，張力會導致架空線產生彈性形變，使架空線的長度增加、截面積減小，而截面積減小的同時截面的慣性矩也減小了。因此，這兩種影響方式在效果上是相反的。就鋼芯鋁絞線的結構特征和其應用特點來說，我們認為該結論可以應用于具體的架空線抗彎剛度識別的實踐當中。

3 架空線抗彎剛度的計算方法

目前在輸電線路領域，求得架空線抗彎剛度的方法主要有以下幾種：

（1）通過實驗得到：對樣品整體進行實驗，從而得到樣品在不同受力狀況下的抗彎剛度值。其優點是數據正確，能真正反映導／地線的抗彎特性；缺點是實驗的工作量較大，費用較高。

（2）通過公式計算得到：目前國內較常用的計算方法有兩種，一是整體計算法，二是分股計算法。

1）整體計算法：

整體計算法就是由下式計算得到：

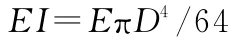
式中，E為導／地線的最終彈性系數（N／mm2），可由導／地線參數表查得；D 為導線外徑（mm）；EI為導線抗彎剛度（N·mm2）。

2）分股計算法：

分股計算法即分別計算鋼股和鋁股的抗彎剛度再求和的方法。分股計算抗彎剛度時，鋁股的彈性系數值約為68.67 GPa，鋼股的彈性系數值約為206 GPa。

兩種理論方法的優點是計算簡便，可以很快得到EI值，但各有其缺點。整體計算法將整根絞線考慮成了一根中間無縫隙的單股線，忽視了導／地線各股之間的空隙對導線整體抗彎剛度性能的影響，因此計算結果與實際數據相比往往偏大；而分股計算法在慣性矩計算方面只是簡單地將各股自身的形心作為其形心來進行計算，忽略了絞線的整體性以及各股之間的聯系和相互影響，這與絞線的實際結構存在很大的區別，其計算結果與實際數據相比往往偏小。

在此我們介紹一種較簡便又切合輸電線路實際的導／地線抗彎剛度的計算方法，其主要思路如下：

（1）將抗彎剛度依導／地線運行狀態的不同分為最小抗彎剛度、最大抗彎剛度和有效抗彎剛度3類。其中最大抗彎剛度對應的是考慮最大慣性矩下的導／地線抗彎剛度，最小抗彎剛度與分股計算法的導／地線抗彎剛度相一致，有效抗彎剛度則是在最大抗彎剛度的基礎上，充分考慮了絞線的結構特征和經驗參數得出的最終結果。

（2）最小抗彎剛度計算公式：

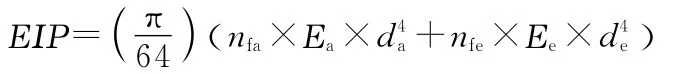
式中，Ea＝Ee＝69.0 k N／mm2（對于 AAC、AAAC或 ACAR導線），Ea＝193.1 k N／mm2、Ee＝69.0 k N／mm2（對于 ACSR 或AACSR導線）；nfa為鋼芯區芯線數量；nfe為包覆區芯線數量；da為鋼芯區線材的直徑（mm）；de為包覆區線材的外徑（mm）。

（3）最大抗彎剛度計算公式：

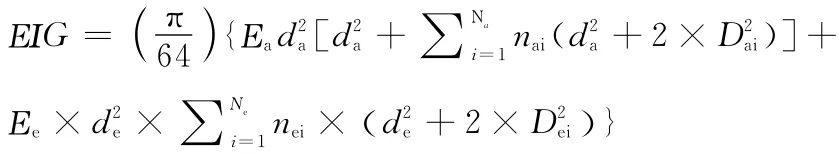
式中，nai為鋼芯區第i層芯線數量；nei為包覆區第i層芯線數量；Dai為鋼芯區第i層外徑（mm）；Dei為包覆區第i層外徑（mm）；Na為鋼芯區的層數（不包括中心芯線）；Ne為鋁線包覆區的層數。

（4）有效抗彎剛度計算公式：

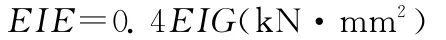
（5）對于導線出口處安裝有護線條部分的有效抗彎剛度的計算，可按下式進行：

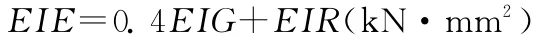
其中：

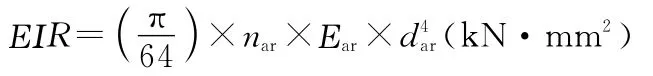
式中，nar為護線條的數量；dar為護線條的外徑（mm）；Ear＝69.0 k N／mm2（對于鋁或鋁合金護線條），Ear＝193.1 k N／mm2（對于鍍鋅鋼護線條）。

4 證例

500 k V五獅線采用的導線為特強鋼芯耐熱鋁合金導線，型號為KTACSR／EST-1000，其中鋼芯區由4層組成，所用材料為特強鋼芯線，各層芯線數分別為1、6、12、18根，鋼芯區外徑為21.0 mm，芯線外徑為3.0 mm；包覆區由3層組成，所用材料為高強度耐熱鋁合金線，各層芯線數分別為18、24、30根，包覆區外徑為46.2 mm，芯線外徑為4.2 mm。此外，懸垂線夾處還安裝有預絞絲護線條，預絞絲護線條所形成的保護區長度為4 m，護線條材料的外徑為7.8 mm，根數為20根。導線平均運行水平張力為123 500 N，測得89 mm處的彎曲振幅為0.12 mm（倒裝法），求其相應的動彎應變值。

（1）最小抗彎剛度計算：

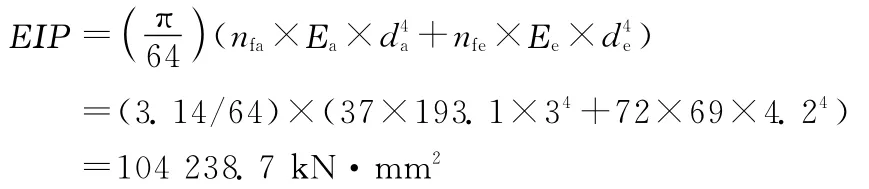
（2）最大抗彎剛度計算：

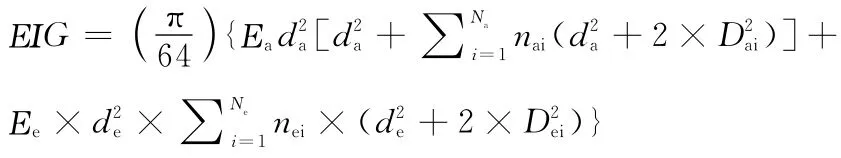
其中：

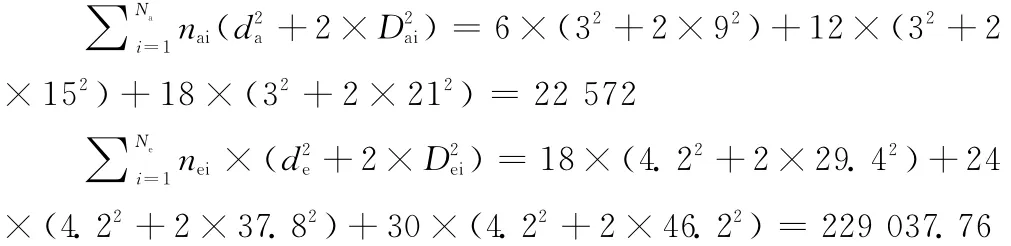
故：

EIG＝（3.14／64）×［193.1×32×（32＋22 572）＋69×4.22×229 037.76］＝15 602 813.1 k N·mm2

（3）有效抗彎剛度計算：

由于導線出口處安裝有護線條，則：

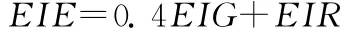
其中：

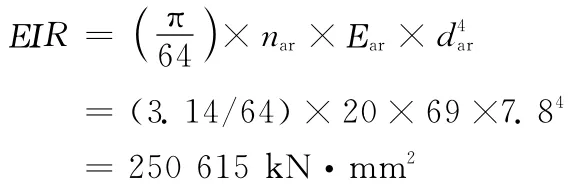
故：

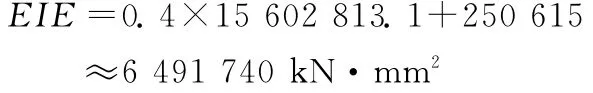
5 結語

本文所推薦的架空線抗彎剛度計算方法簡便有效，且充分考慮了架空線本身的結構特征和應用環境的特點，可為導／地線微風振動計算、跳線抗彎剛度計算等應用領域提供一種快速、準確獲得抗彎剛度參數的途徑。

［1］潘忠華，徐乃管，陳露娟.懸垂線夾出口處動彎應變與彎曲振幅關系的探討［J］.中國電力，1982，15（12）

［2］謝曉峰.索的抗彎剛度識別方法研究［D］.長沙：中南大學，2012