ARIMA時間序列在乙肝發病預測中的應用

北京市昌平區疾病預防控制中心(102200) 王 濤 苑新海 朱宗龍

傳染病預測是根據傳染病發生、發展規律及有關因素，用分析判斷和數學模型等方法對傳染病的發生、發展和流行趨勢作出預測，是制定預防和控制傳染病的長期或近期應對策略的前提[1]。本文以昌平區乙肝的月發病數為基礎，應用時間序列分析法對其發病情況建模，并預測其發病趨勢，為早期發現乙肝的流行及制定相關防治策略提供依據。

方法和原理

1.資料

北京市昌平區2005-2012年乙肝發病數據來源于疾病監測信息報告管理系統。同時由于昌平區人口基數較大且相對穩定，最終確定以乙肝發病數代替發病率來進行預測分析。

2.方法

(1)基本思想

標準的ARIMA模型為ARIMA(p,d,q)(P,D,Q)s，其中p、q分別表示自相關函數(ACF)和偏自相關函數(PACF)的階，d表示差分的次數，P、Q、D分別表示季節性自相關函數和偏自相關函數的階和差分的次數，s表示季節性的周期[2-3]。

(2)建模過程

①數據預處理。首先判斷原序列是否平穩，若為非平穩序列，首先變換為平穩序列，根據變換后序列的自相關和偏自相關圖，確定非季節差分階數d和季節差分階數D。②模型參數估計。根據變換后平穩時間序列的自相關和偏自相關圖，估計模型的p、P、q、Q的值，采用最大似然估計或最小二乘法估計等對初步估計模型進行檢驗。模型參數必須通過t檢驗，且全部特征根的倒數都小于1[4]。③模型診斷檢驗。模型參數估計后，對模型殘差是否為白噪聲進行檢驗，若殘差序列不是白噪聲序列，意味著殘差序列還存在有沒被提取的信息，需要進一步改進模型。④模型的篩選。為了得到最佳模型，可借助擬合優度統計量來比較各個模型的優劣，最常用的是調整后的決定系數、AIC和SC統計量。⑤模型的預測。運用模型預測未來某一時間段的乙肝發病情況。

(3)統計分析

使用SPSS 17.0軟件進行統計分析。將北京市昌平區2005-2012年乙肝月發病數據建立ARIMA模型進行時間序列分析。

結 果

1.發病情況及變化趨勢

對北京市昌平區2005-2012年乙肝月發病數(Zt)曲線(圖1)直觀分析可看出，昌平區除2006年和2007年乙肝高發外，其余各年發病較為平穩，全年均有發病。

2.序列平穩性判斷

序列平穩性檢驗是建模的重要前提。除從序列圖(圖1)判斷原始序列存在長期趨勢，同時采用游程檢驗法對時間序列進行平穩性檢驗，得出游程數為16，檢驗統計量z=-6.446，P=0.000，表明其為非平穩性時間序列。

3.數據預處理

從原始序列圖和游程檢驗結果可看出原始數據為非平穩序列，因此對原始序列進行自然對數轉換和一階非季節性差分和一階季節性差分，以消除趨勢和季節影響而達到平穩化，使序列呈現為一組平穩的隨機數據以符合時間序列分析的條件[5]。從差分后序列的序列圖(圖2)可以看出，近似為平穩序列。

圖1 昌平區2005-2012年乙肝月發病數(Zt)原始序列圖

4.模型參數估計

由于原始時間序列經一階非季節性差分和一階季節性差分后達到平穩，因此d=1、D=1。首先建立ARIMA(2,1,1)(2,1,1)12模型，經檢驗，變量AR(2)、SAR(2)的P>0.05，沒有通過t檢驗，然后考慮刪除變量AR(2)、SAR(2)，嘗試建立ARIMA(0,1,1)(0,1,1)12模型，經檢驗，該模型的所有參數均通過了t檢驗(表1)。

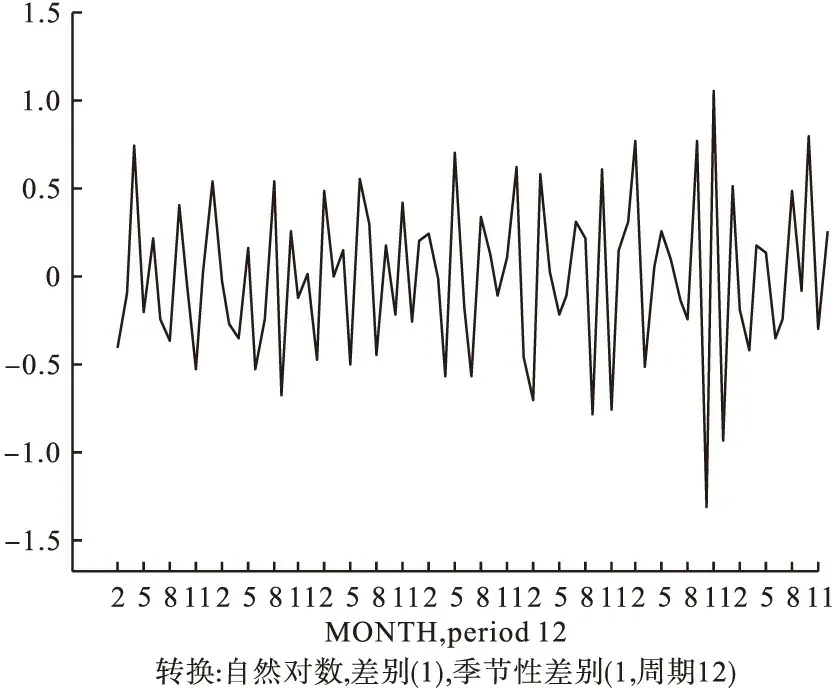
圖2 昌平區2005-2012年乙肝月發病數差分后序列圖

表1 不同ARIMA模型的檢驗結果

5.模型診斷檢驗

對ARIMA(0,1,1)(0,1,1)12模型殘差進行是否為白噪聲的LB統計量檢驗[6]，最大滯后期m取16，Q15=8.428，P=0.935>0.05，故不能拒絕殘差序列為白噪聲的原假設，檢驗通過。

6.模型的篩選

對ARIMA(0,1,1)(0,1,1)12模型的擬合優度進行分析，ARIMA(0,1,)(0,1,1)12模型的自相關(ACF)和偏自相關(PACF)函數與0差異無統計學意義，且均在95%可信區間內(圖3)，說明擬合效果較好。

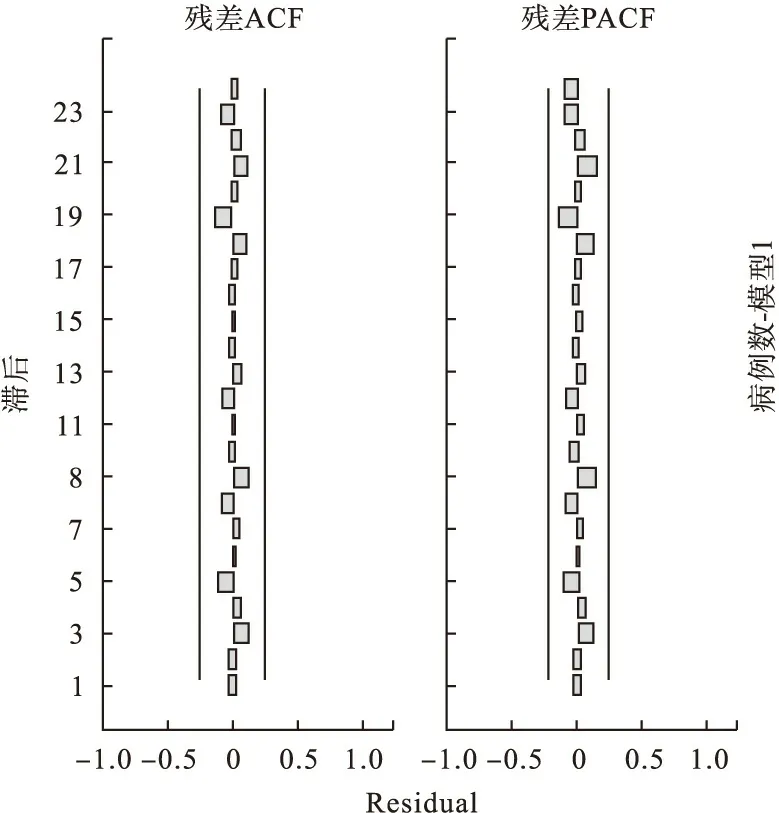
圖3 殘差ACF和殘差PACF相關系數

7.模型的預測

用ARIMA(0,1,1)(0,1,1)12模型對原序列進行擬合可見(圖4)，模型預測值的動態趨勢與實際值基本一致。

圖4 ARIMA(3,1,0)(3,1,0)12模型預測擬合圖

討 論

時間序列方法是研究預測對象在一定時期內的變動過程，從中尋找和分析事物的變化特征和發展趨勢，本研究采用時間序列分析方法對昌平區2005-2012年乙肝的月發病數據進行了動態分析研究，建立了預測模型，并對所建立的模型進行了評價。

據全國法定傳染病監測數據顯示，近年來乙肝發病率呈逐年遞減的趨勢，但慢性乙肝在全世界成人的死因中趨于首位，特別是在慢性乙肝感染率高的國家[7]。因此建立預測模型對乙肝流行規律進行定量預測以進行早期預警，對于乙肝防控有重大意義。本

文通過對北京市昌平區2005-2012年乙肝月發病數時間序列進行分析，建立了ARIMA(0,1,1)(0,1,1)12模型。模型較好的擬合了昌平區乙肝月發病數的變化規律，顯示出較高的預測精度，說明利用ARIMA模型預測乙肝的流行趨勢是可行的，但ARIMA建模法假定時間序列為未來的發展模式與過去的模式是一致的，因此往往只適于作短期預測。

本文證實了ARIMA模型法可較好的用于乙肝發病的預測，但應用時需注意時間序列方法的應用條件。ARIMA應用前提是時間序列的平穩性，實際工作中數據往往是非平穩序列，需對序列進行預處理，使之達到平穩的要求。其次，ARIMA模型要求至少有50個時間點的數據或7～8個周期的數據。同時疫情受諸多未知隨機因素的影響，單次分析所建立的ARIMA模型應不斷補充新的實際數據，對模型進行修正或重新擬合，以提高預測敏感性。另外除從數據自身特征尋找預測模型外，還應結合具體的外部信息，識別出因突發事件引起的序列值波動，以便于對預測結果進行解釋。同時規范的、統一的乙肝病例診斷、報告標準是對乙肝進行預測預警的基礎和前提[8]，慢性乙肝病例的重復就診和報告，乙肝病毒攜帶者也作為病例報告，以及由于乙肝復雜的臨床表現，不同醫生或醫療機構對乙肝病例報告標準的執行存在差異，這些都會影響乙肝發病預測。

參 考 文 獻

1.尹志英，方春福.傳染病預測預警方法探討.中國衛生統計，2010，27(2)：218-220.

2.陳峰，王嘯天，朱和新.混合指數周期模型及其在疾病季節性分析中的應用.南通醫學院學報，1996，16(3)：301-303.

3.Peng Z,Bao C,Zhao Y,et al.Weighted markov chains for forecasting and analysis in incidence of infectious diseases in Jiangsu Province,China.Journal of Biomedical Research,2010,24(3):207-214.

4.中國人民銀行調查統計司主編.時間序列X-12-ARIMA季節調整—原理與方法.北京：中國金融出版社，2006:59-60.

5.郭建娥，劉桂芬.構建山西省太原市痢疾發病率的ARIMA模型.疾病監測，2007，34(4):154-155.

6.易丹輝.數據分析與EVIEWS應用.北京：中國人民大學出版社，2008:137-140.

7.Schafer DF,Sorrell MF.Hepatocellular carcinoma.Lancet,1999,353(10):1253-1257.

8.崔樹峰，馬建新，李書明.時間序列分解法在北京市朝陽區細菌性痢疾周報告發病率預測中的應用.中國衛生統計，2009，26(6):583-591.