變階變正則化APA在回聲抵消中的應用

冀常鵬 ，姬紅紅 ，郭偉平

JI Changpeng1，2,JI Honghong1,GUO Weiping1

1.遼寧工程技術大學 研究生院，遼寧 葫蘆島 125105

2.遼寧工程技術大學 電子與信息工程學院，遼寧 葫蘆島 125105

1.Institute of Graduate,Liaoning Technical University,Huludao,Liaoning 125105,China

2.School of Electronic and Information Engineering,Liaoning Technical University,Huludao,Liaoning 125105,China

1 引言

隨著視頻會議、語音通信技術和網絡技術的發展以及人們生活水平的日益提高，對通信方式和通信質量的要求也在不斷提高。仿射投影算法在無線信道均衡器、回聲抵消、噪聲消除和語音增強[1]等方面有著廣泛的應用。由于通信環境的多樣性、復雜性和自適應濾波器的特點，對所采用的仿射投影算法（APA）的性能要求也很高。

歸一化最小均方誤差（NLMS）僅僅根據當前的遞歸方程更新權重而APA是根據最新的K個遞歸值和觀察值更新權值，所以APA可以看成是NLMS的規范化[2]。對于經典的APA，步長同時控制著算法的收斂速率和穩態誤差。由文獻[3-4]可知，為了滿足收斂速度快和穩態誤差小這對相互矛盾的要求，已根據不同的應用要求提出了許多變步長的改進方法。然而，在這些APA中秩虧矩陣需要求逆。為了避免秩虧矩陣求逆需要引入正則化因子，它為算法數據的穩定性提供了保證。文獻[5]中，提出了變正則化的仿射投影算法。相對于傳統的APA假設后驗誤差為0，文獻[5]考慮了噪聲的統計特性，為了減小自適應濾波器的真實值與估計值之間的誤差，文中假設后驗誤差等于噪聲方差。因此將噪聲的統計特性考慮到自適應濾波器的設計中，利用瞬時估計推導出最佳的正則化因子。通過逐漸調整正則化因子可以改善收斂速度和穩態誤差，正則化因子的應用使得APA對外界擾動和模型不確定性具有魯棒性。文獻[6]提出可變階數的APA即E-APA，文中利用穩態誤差的瞬時值，通過比較輸出均方誤差與閾值的大小來自動調整當前的階數。E-APA不僅可以很可觀地改善穩態誤差和收斂速度之間相互矛盾的現狀，而且由于輸入矢量的數目減少故其整體計算量減小。另外在無法獲得確切的噪聲方差對噪聲進行評估和抑制的情況下，E-APA也具有很強的魯棒性。文獻[7]的不定階變步長仿射投影算法在調整投影階數時，通過不斷減小迭代步長的方式，改善了收斂速率和穩態失調性能，同時還能降低算法復雜度。由于階數越大收斂越快復雜度也越大，步長越大收斂越快穩態誤差也越大。

APA通過重復利用信號樣值的方法，在輸入數據相關性較高時有很快的收斂速度。然而，APA在迭代過程中計算復雜度較高，穩態失調性能也比NLMS算法要差。變階數和變步長的相互調節難以達到最佳匹配狀態，所以對算法性能改善程度不高。而對于單純變步長算法的復雜度很高[8]。本文將從變階和變正則化因子兩方面出發推導出一種新的仿射投影算法，并驗證其性能的優越性。

2 傳統的APA模型

自適應濾波器的權系數為 w(n)=[w0(n)，w1(n)，…，wL-1(n)]T，n時刻的輸入信號向量為 x(n)=[x(n)，x(n-1)，…，x(n-L+1)]T，期望響應信號為 d(n)=[d(n)，d(n-1)，…，d(n-K+1)]T，K為濾波器的投影階數，L代表FIR系統的階數 A(n)=[x(n)，x(n-1)，…，x(n-K+1)]T。 wopt是待估計的未知矩陣，設w(n)為n時刻對wopt的估計值，v(n)為噪聲信號。則仿射投影算法的基本公式[5-7]如下：

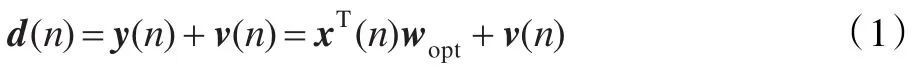
經典的濾波器權系數的更新公式為：

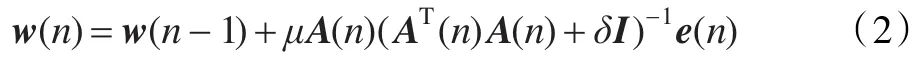
其中I為K×K的單位矩陣。誤差公式為：

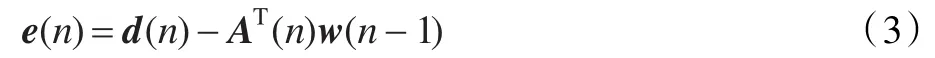
(·)T為矩陣的轉置。μ為步長因子，e(n)為信號誤差，后文中也稱為先驗誤差。δ為正則化因子，它不僅可以有效避免秩虧矩陣AT(n)A(n)的倒置，也對傳統仿射投影算法的收斂速度和穩態誤差的調節發揮著重要的作用。

3 算法的優化

一般傳統算法的后驗誤差認為為零，即忽略噪聲的存在。在此將噪聲的統計特性考慮到自適應過程中。而且通過調節正則化因子來盡量減小穩態誤差以增加收斂的穩定性[9]。通過調節投影階數來加快算法的收斂速度、適時地減少計算的復雜度。雖然算法階數越大，收斂速度越快，但此時穩態誤差也越大，而通過變正則化因子和可變階數的協同調節，使改進的算法具有較好的性能。

為了增加此算法的穩定性，減小穩態誤差，用可變的δ(n)來修正正則化因子[5]，所以式（2）就可以表示為：

w(n)=w(n-1)+μA(n)(AT(n)A(n)+δ(n)I)-1e(n)（4）其中步長為1，設 S(n)=(AT(n)A(n)+δ(n)I)-1，所以 w(n)=w(n-1)+A(n)S(n)e(n)，設 e(n)為先驗誤差矢量，ε(n)為后驗誤差矢量，其表達式為ε(n)=d(n)-AT(n)w(n)。由式（4）可得先驗誤差和后驗誤差的關系為ε(n)=(I-AT(n)·A(n)S(n))e(n)。把e(n)代入ε(n)可得到后驗誤差的表達式為ε(n)=AT(n)(wopt-w(n))+v(n)。理想情況下后驗誤差應該為零，事實上，噪聲信號是存在的，很明顯只有wopt-w(n)=0，即wopt=w(n)才能使后驗誤差最小。因此有ε(n)=v(n)。對其求一階范數的平方再求期望得E{||ε(n)||2}=E{||v(n)||2}。即

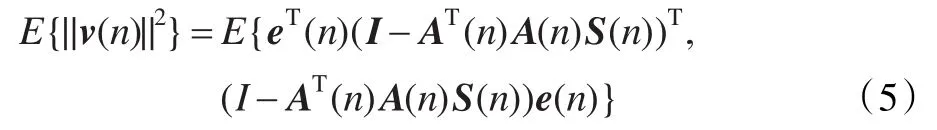
利用特征值的分布化簡式（5），把格拉姆矩陣寫成特征值分布的矩陣形式：

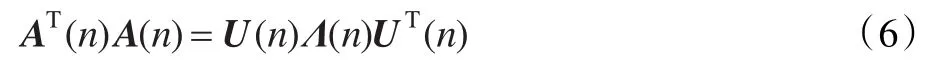
Λ(n)是由AT(n)A(n)的特征值組成的對角矩陣，U(n)是AT(n)A(n)的特征向量。所以

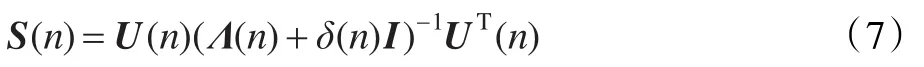
設一矩陣的第 k 個對角元素為(δ(n)/(λk(n)+ δ(n)))2，則該矩陣的對角矩陣為：

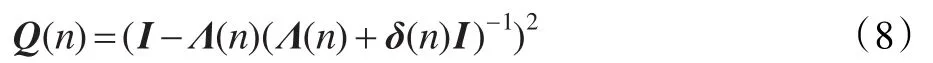
把式（6）～（8）代入式（5）可得后驗誤差與噪聲的關系為：

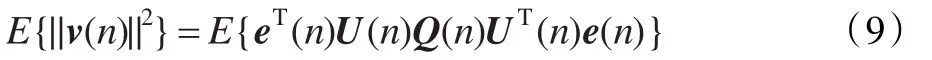
上式的推導是建立在后驗誤差和噪聲矢量相等的基礎上的，它高度依賴于矩陣AT(n)A(n)的特征值分布。因此不可能利用這種方法來獲取可變的正則化因子。但可以用一些簡單易行的方法進行逼近。由于AT(n)A(n)的第k個對角元素是輸入信號的二階范數[5]，通過近似推理可以得到：

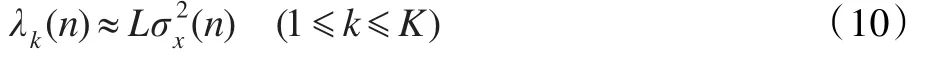
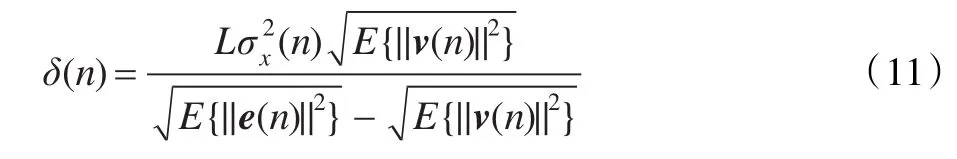
由式（11）可知，在自適應算法的開始階段，先驗誤差e(n)的值很大，而此時起主要作用的是E{||e(n)||2}，所以E{||e(n)||2}的值也很大，使得δ(n)值很小，所以收斂速度很快。而在自適應進程中隨著算法逐漸地趨于穩定E{||e(n)||2}的影響逐漸減小，而E{||v(n)||2}的改變量增大，所以此時δ(n)的值主要受 E{||v(n)||2}的影響，所以δ(n)不斷增加，自適應濾波器的系數開始緩慢調節，收斂速度趨于穩定。

一般情況下，由于 ||e(n)||＞||v(n)||，所以 δ(n)≥0 。當算法開始收斂時，||v(n)||和||e(n)||之間的差距越來越小，δ(n)將會出現負值[10]。為了避免 δ(n)＜0 ，可取 δ(n)=δ(n-1)。且在實際計算中可用瞬時逼近的方法來計算和其中為矩陣的跡，α 是遺忘因子為一常數，取值為0.998，且有了變正則化因子的保證，穩態誤差方面可以有所緩解，而快速的收斂速度是算法收斂性能恒久不變的追求，所以本文繼續探討收斂速度的問題。在仿射投影算法中，投影階數越大，收斂速度越快，但穩態誤差越大，計算復雜度越高。可變階數的仿射投影算法根據穩態均方誤差來調整當前階數，不僅能有效解決收斂速度與穩態失調的矛盾[11]，還可以有效地降低算法的計算量。

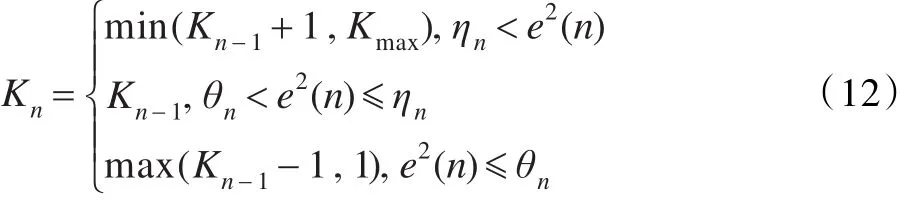
采用文獻[6]的方法求取其階數Kn，式中ηn是第n次迭代過程中的誤差上限，θn是第n次迭代過程中的誤差下限。Kn的取值范圍1≤Kn≤Kmax，Kmax為最大投影階數，Kmax≤L。在算法計算過程中，ηn和θn的計算公式采用文獻[6]中的表達式計算，即2)/(2-μ(n-1))。但是此算法要求步長始終為1，所以可得

由式（12）可以看出，在迭代的初始階段系統誤差很大，使得正則化因子較大，而且初始階數較高，因此收斂速度較快；當濾波算法收斂后，階數隨著需要有所降低，失調量較小，誤差降低算法較穩定。在迭代過程中本文算法的階數與傳統APA算法相比更具靈活性，使得在開始階段計算量稍大但也低于傳統APA，但在收斂后該算法的計算量將伴隨著階數的減少而大大降低。傳統的仿射投影算法迭代一次的計算量是Ο(K2L)，本文的計算復雜度為Ο(K2L)，而且階數是適時調整，所以改進的算法更有優越性。

4 仿真結果

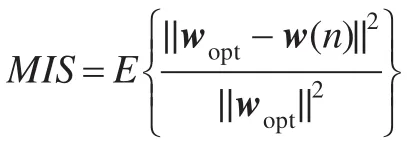
圖1所示為利用語音信號模擬的回聲路徑，其沖擊響應階數為64階。

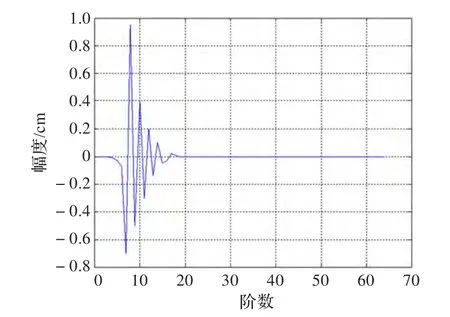
圖1 模擬的回聲路徑

圖2和圖3分別顯示的是AR（0.8）和ARMA（2，2）的收斂曲線，為方便仿真結果容易比較，均取SNR=25 dB，步長為1，α=0.998。由圖2可知本文算法的收斂速度和穩態誤差均優于文獻[5-6]。而圖3顯示了本文算法具有較快的收斂速度，穩態誤差比文獻[6]的算法稍低但明顯優于文獻[5]。綜合上述兩種仿真可知本文算法的優越性，而且下面會繼續討論。

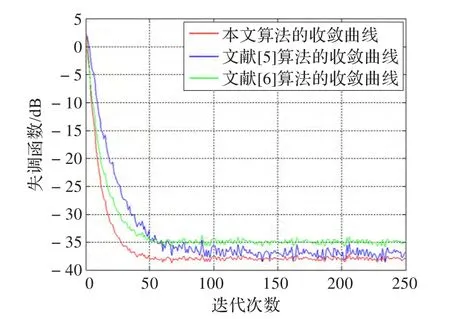
圖2 AR（0.8）過程的三種算法收斂性曲線圖

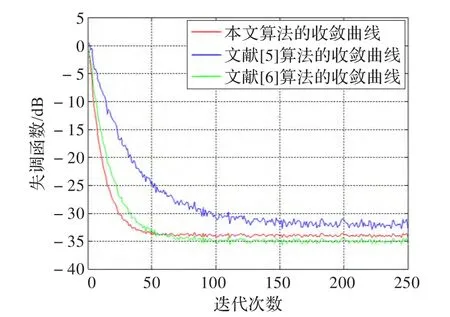
圖3 ARMA（2，2）過程的三種算法收斂性曲線圖

圖4顯示了文獻[5-7]以及本文算法的收斂曲線。該實驗是在實驗室環境中進行的，其環境模擬的回聲路徑如圖1所示。在文獻[5]、[7]中 SNR=25 dB，α=0.998；在文獻[6]中設初始階數為30，步長為1。從收斂速度方面來看，在收斂曲線的初始階段，通過調節投影階數來加快算法的收斂速度，總體來說圖中三種算法均表現了較快的收斂速度，但文獻[5]的變正則化因子的APA收斂速度相比較而言較慢，本文提出的算法和文獻[7]中算法的收斂速度相當，且比文獻[6]的變階數的APA略有優勢但三者都比文獻[5]中的算法收斂速度快；在收斂的穩定階段，階數減小算法整體收斂速度趨于穩定，主要顯示了通過調節正則化因子來盡量減小穩態誤差的性能，由圖可知變正則化因子的APA的收斂幅度要大于變階數的APA但遠低于本文算法的收斂幅度。從穩態誤差方面看，在整個收斂過程中文獻[7]的不定階變步長算法穩態誤差最大，本文所提算法的穩態誤差即失調量最小，算法整體變化也相對穩定。即在算法收斂穩定后，在相同的條件下本文改進算法失調量明顯優于單純的變階或變正則化和不定階變步長算法的失調量，對應于回聲抵消的過程中系統的穩定性能更好，則回聲抵消系統很穩定，效果也更好。

圖4 四種算法失調函數的曲線圖

5 結論

現如今隨著人們對通話質量要求的不斷提高，回聲抵消的性能也越來越受到人們的重視。而APA在回聲抵消中具有非常重要的地位。針對已有的APA算法收斂速度慢和穩態誤差大等問題，本文提出了一種可變階數和可變正則化因子相結合的算法。仿真結果表明通過變階數可調節算法的收斂速度，加快算法收斂，與此同時變正則化因子的引入可在快速收斂的基礎上減小穩態誤差，使算法更穩定。改善了回聲抵消中快的收斂速度和小的穩態誤差不能兼得的現狀。該算法與已有的算法相比在收斂速度、失調性能以及計算量方面都有很好的表現，更能滿足人們對通話質量的需求。

[1]Yang J G，Sobelman E.Efficient μ-law improved proportionate affine projection algorithm for echo cancellation[J].Electronics Letters，2011，47（2）：73-74.

[2]Yang Zengli，Zheng Y R，Grant S L.Proportionate affine projection sign algorithms for network echo cancellation[J].IEEE Trans on Audio，Speech and Language Processing，2011，19（8）：2273-2284.

[3]Shin H C，Sayed A H，Song W J.Variable step-size NLMS and affine projection algorithms[J].IEEE Signal Processing Letters，2004，11（2）：132-135.

[4]Rey H，Vega L R，Tressens S，et al.Variable explicit regularization in affine projection algorithm：robustness issues and optimal choice[J].IEEE Trans on Signal Processing，2007，55（5）：2096-2109.

[5]Yin Wutao，Mehr A S.A variable regularization method for affine projection algorithm[J].IEEE Trans on Circuits and Systems II：Express Briefs，2010，57（6）：476-480.

[6]Kim S，Kong Se-jin，Song Woo-jin.An affine projection algorithm with evolving order[J].IEEE Signal Processing Letters，2009，16（11）：937-940.

[7]趙愉，李鋒.不定階變步長仿射投影算法[J].信息與電子工程，2011，9（1）：64-68.

[8]趙愉，彭最亮，李鋒.一種新的變階仿射投影算法[J].計算機工程與應用，2012，48（16）：145-147.

[9]Paleologu C，Benesty J，Ciochina S.Regularization of the affine projection algorithm[J].IEEE Trans on Circuits and Systems II：Express Briefs，2011，58（6）：366-370.

[10]Myllyl? V，Schmidt G.Pseudo-optimal regularization for affine projection algorithms[C]//ICASSP，2002：1917-1920.

[11]Shin H，Sayed A H.Mean-square performance of a family of affine projection algorithms[J].IEEE Trans on Signal Processing，2004，52（1）：90-102.