基于積分的數(shù)值微分算法

徐會(huì)林，郜星軍

(河南理工大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院，河南 焦作454000)

0 前言

數(shù)值微分，即由給定函數(shù)的測(cè)量數(shù)據(jù)近似求其導(dǎo)數(shù)，這類問(wèn)題在科學(xué)研究及工程實(shí)踐中有廣泛的應(yīng)用價(jià)值。如在磁共振電阻抗成像技術(shù)(MREIT)中，介質(zhì)的導(dǎo)電率是利用生物組織內(nèi)部電流產(chǎn)生的磁場(chǎng)信息重建的。基于主磁場(chǎng)方向磁感應(yīng)強(qiáng)度的調(diào)和Bz算法是當(dāng)前主流的導(dǎo)電率重建算法，而如何由磁感應(yīng)強(qiáng)度的測(cè)量數(shù)據(jù)計(jì)算其二階導(dǎo)數(shù)是關(guān)鍵步驟［1］，數(shù)值微分的具體應(yīng)用還體現(xiàn)在數(shù)字圖像特征檢測(cè)問(wèn)題［2］、期權(quán)定價(jià)問(wèn)題［3］、放射性廢棄物的存儲(chǔ)問(wèn)題［4］等方面。

數(shù)值微分問(wèn)題的求解，除標(biāo)準(zhǔn)的正則化方法外［5～8］，還有一些其特有的方法，如有限差分法［9］、平滑化方法［10］等。眾所周知，微分和積分是互逆的2種基本運(yùn)算。積分的計(jì)算通常要借助微分實(shí)現(xiàn)，反過(guò)來(lái)，也可利用積分求微分，其實(shí)質(zhì)是將微分運(yùn)算等價(jià)轉(zhuǎn)化為第一類積分方程的求解問(wèn)題［11，12］。

本文將基于微分與積分之間的互逆關(guān)系，構(gòu)造數(shù)值微分的實(shí)現(xiàn)算法。通過(guò)把數(shù)值微分問(wèn)題等價(jià)轉(zhuǎn)化為第一類積分方程的求解問(wèn)題，給出了一元函數(shù)前兩階導(dǎo)數(shù)的近似計(jì)算方法，并通過(guò)數(shù)值算例說(shuō)明了解的數(shù)值有效性。

1 一階數(shù)值微分算法

設(shè)一元函數(shù)f(x)∈C1［0，1］，u(x)為其一階導(dǎo)函數(shù)，即u(x)=f'(x)∈C［0，1］，則函數(shù)u和f滿足第一類的Volterra型積分方程

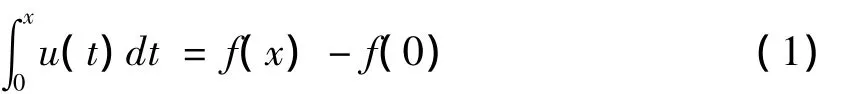
不失一般性，設(shè)f(0)=0，則有

此時(shí)，求導(dǎo)數(shù)u的問(wèn)題就轉(zhuǎn)化為積分方程(2)的求解問(wèn)題［11］。在實(shí)際問(wèn)題中，函數(shù)f(x)的表達(dá)式一般是未知的，已知的只是其在某些離散點(diǎn)上的取值。……