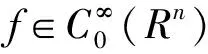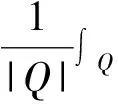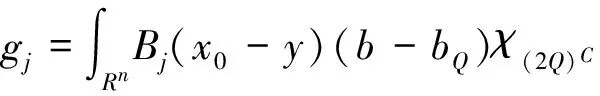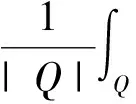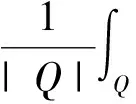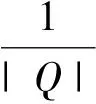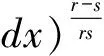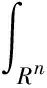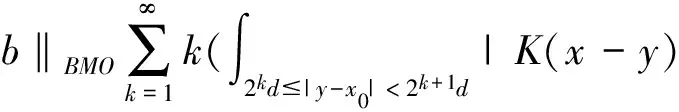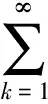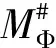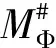一類滿足?rmander條件的奇異積分算子交換子的Lp有界性
曹 美 陽
(江西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,江西 南昌 332200)
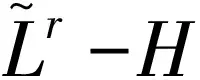
曹 美 陽
(江西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,江西 南昌 332200)
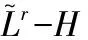
交換子;奇異積分算子;sharp極大函數(shù)
1 引言和主要結(jié)果
奇異積分算子及其交換子的有界性在調(diào)和分析和偏微分中有重要的應(yīng)用。在文獻(xiàn)[1,2]中,Coifman和Janson等分別證明了由奇異積分算子和BMO函數(shù)生成的交換子在Lp(Rn)(1 定義1:設(shè)函數(shù)K∈L2(Rn)。存在常數(shù)C0>0使得: (2)|K(x)|≤C|x|-n; 文獻(xiàn)[5,6]中考慮了一類變形的H?rmander的條件,并且得到相應(yīng)奇異積分算子的加Lp有界性。 定義2:設(shè)函數(shù)K∈L2(Rn)滿足條件: (1)‖K‖L∞≤C; (2)|K(x)|≤C|x|-n; (4)對于1 ander條件。張璞等在文獻(xiàn)[8]中證明滿足上述Lr-H?rmander條件的奇異積分算子是Lp有界的。 令b為Rn上的局部可積函數(shù),其與T生成的交換子定義為: Tb(f)(x)=b(x)Tf(x)-T(bf)(x)。 本文主要結(jié)果如下。 首先,回顧一些基本定義。 定義3:令Φ={φ1,…,φl}為Rn上的有界函數(shù),對局部可積函數(shù)f,定義Φ sharp極大函數(shù)為 φi(xQ-y)|dy, 其中下確界取遍所有的1重復(fù)數(shù){c1,…,cl},xQ為方體Q的中心。 本文中,Q表示Rn中的方體,給定方體Q和Rn上的局部可積函數(shù)f,令 和 眾所周知(見文獻(xiàn)[3,7]), 如果M#(f)(x)屬于L∞(Rn),則稱函數(shù)f屬于BMO(Rn),且令 ‖f‖BMO=‖M#(f)‖L∞。 根據(jù)文獻(xiàn)[7],有 ‖f-f2kQ‖BMO≤Ck‖f‖BMO。 記 下面引入一些證明過程中需要的引理。 引理1[8]:令T為定義1所述奇異積分算子,則T在Lp(Rn)(1 f(y)dy。 固定方體Q=Q(x0,d),使得x∈Q,則 Tb(f)(x)=(b-bQ)Tf(x)-T((b-bQ)f) (x) 因此 下面分別估計(jì)Ⅰ與Ⅱ。首先估計(jì)Ⅰ。利用H?rmander不等式, 為估計(jì)Ⅱ,將f分解:f=f1+f2,其中f1=fχ2Q(x),f2=f-f1。則 再分別估計(jì)Ⅱ1和Ⅱ2。選取1 對Ⅱ2,當(dāng)x∈Q時(shí),有 針對Ⅱ21,利用|b2k+1Q-b2Q|≤k‖b‖BMO, 根據(jù)H?lder不等式,有 對Ⅱ22,取t>r,使用H?lder不等式,有 綜上所述,得 最后證明定理2。 定理2的證明:在定理1中,選取1 [1] Coifman R R,Rochberg R,Weiss G.Fractorization theorems for Hardy spaces in several variables[J].Ann.of Math,1976,103:611-635. [2]Janson S.Mean oscillation and commutators of singular integral operators[J].Ask.Math,1978,16:263-270. [3]Trujillo-Gonzalez R.Weighted norm inequalities for sing- ular integral operators satisfying a variant ofH?rmander′scondition[J].Comment.Math.Univ.Carolin,2003,44:137-152. [4]Pe′rezC.Endpoint estimate for commutators of singular integral operators[J].J.Func. Anal,1995,128:163-185. [5]Garcia-Cuerva J,Rubio de Francia J L.Weighted Norm Inequalities and Related Topics[J].North-Holland Math.Amsterdam,16,1985. [6]Grubb D J,Moore C N.A Variant ofH?rmander′s condition for singular integrals[J].Colloq.Math,1997,73:165-172. [7]Lorente M,Riveros M S,de la Torre A.Weighted estimates for integral operators satisfyingH?rmander′s condition of Young type[J].Journ Fourier Anal Appl,2005,(11):495-509. [8]張 璞,張代清.變形H?rmander條件與奇異積分算子的加權(quán)估計(jì)[J].數(shù)學(xué)學(xué)報(bào),2……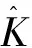
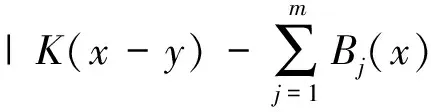
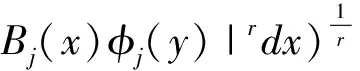
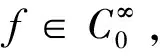
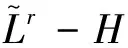
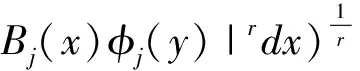
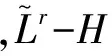
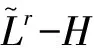
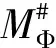
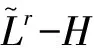
2 預(yù)備知識(shí)和需要的引理
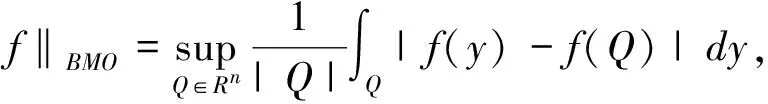
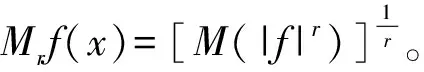
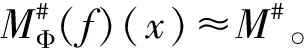
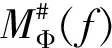
3 定理的證明