基于MIV與RBF神經網絡的滾珠絲杠故障診斷*

溫國強 文 妍 譚繼文

(青島理工大學，山東 青島 266033)

滾珠絲杠是數控機床中最常使用的關鍵傳動元件，具有高精度、可逆性和高效率的特點［1］。滾珠絲杠若出現故障，將會直接影響到數控機床的加工精度，造成產品質量下降甚至報廢，損失嚴重。因此，若能在滾珠絲杠故障形成早期進行正確及時的診斷，對其生產效率與產品質量的提高大有裨益。

在傳統診斷方法中，通常是對原始故障信號進行特征提取后，將所有特征值作為傳統BP 神經網絡或者支持向量機的輸入參量進行模式識別。這種方法輸入參量多、診斷過程復雜，同時，由于BP 網絡容易陷入局部極小值，而且收斂速度相對較慢或無法收斂，診斷精度相對較低。本文引入平均影響值(MIV)方法對故障特征進行篩選處理，去除冗余特征，將剩余特征作為故障識別的輸入參量;基于具有逼近精度高、無局部極小問題且收斂速度快等特點的徑向基(RBF)神經網絡建立了數控機床滾珠絲杠故障識別模型，有效提高了故障診斷精度和速度，效果良好。

1 MIV 算法

1.1 平均影響值(MIV)

平均影響值(MIV，Mean Impact Value)，是一種目前被認為是在神經網絡中評價變量相關性的最好指標之一［2］。該算法可用于確定輸入變量對輸出變量的影響大小，其符號代表相關的方向，絕對值代表影響的大小。

1.2 計算思想［3］

(1)用原始樣本S 對BP 神經網絡進行訓練，并對訓練集S 進行回歸預測;

(2)在網絡訓練結束后，將訓練樣本S 中每一自變量在其原值的基礎上分別加、減10%構成兩個新的訓練樣本S1 和S2;

(3)利用構建好的BP 網絡，對樣本Sl 和S2 分別進行仿真，得到兩個仿真結果Ml 和M2;

(4)求出Ml 和M2 的差值，即為變動該自變量后對輸出產生的影響變化值(簡稱W);

(5)將W 按觀測例數平均得出該自變量對于因變量的平均影響值MIV，同理可計算出各個自變量的MIV 值;

(6)根據MIV 絕對值的大小為各自變量排序，得到各自變量對網絡輸出影響相對重要性的位次表，從而判斷出輸入特征對于網絡結果的影響程度，即實現了變量篩選。

2 RBF 神經網絡

2.1 RBF 網絡

RBF 神經網絡是1985 年由Powell 提出的多變量差值的徑向基函數(Radial Basis Function，簡稱RBF)方法。該網絡是一種性能優良的前饋型神經網絡，具有唯一的最佳逼近特性，且無局部極小問題存在［4］。其結構與多層前向網絡相似，是三層的前向網絡，由一個輸入層、一個隱含層、一個輸出層組成。

2.2 RBF 網絡算法

學習算法具體步驟如下［5］:

步驟1:基于K-均值聚類方法求取基函數中心c。

(1)將網絡進行初始化設置:隨機選取h 個訓練樣本作為聚類中心ci(i=1，2，…，h)。

(2)利用最近鄰規則將輸入的訓練樣本集合進行分組:按照xp與中心ci之間的歐式距離將xp分配到輸入樣本的各個聚類集合vp(i=1，2，…，h)中。

(3)聚類中心作重新調整:對每個聚類集合vp中的訓練樣本求取平均值，構成新的聚類中心ci，如果ci沒有改變，則此時的ci就是RBF 神經網絡最終的基函數中心，否則返回(2)，進行下一輪的中心求解。

步驟2:求解方差σi。

選取高斯函數作為該RBF 神經網絡的基函數，方差σi可由下式求解:

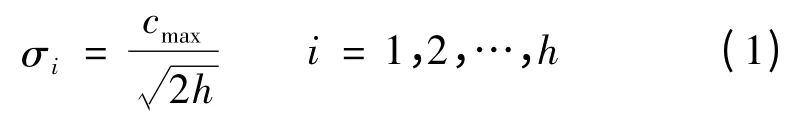
式中，cmax是所選取中心之間的最大距離。

步驟3:求取隱含層和輸出層之間的權值。

運用最小二乘法可直接計算出隱含層到輸出層之間神經元的連接權值，計算公式如下:

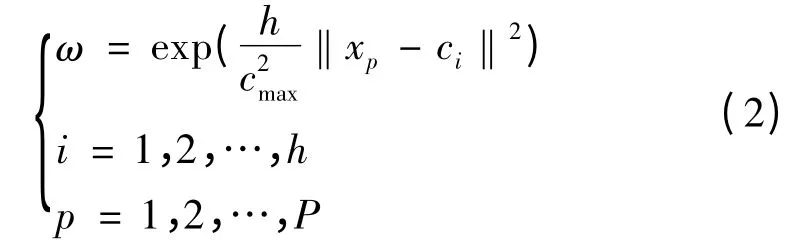
3 滾珠絲杠故障診斷實例與建模

3.1 信息采集

將加速度傳感器布置于絲杠兩端軸承座處，采集工作狀態下的滾珠絲杠振動信號。為獲取較全面的故障信息，采用3 個傳感器測量X(徑向)、Y(軸向)、Z(徑向)3 個方向的信號，如圖1 所示。

本實驗用正常絲杠、滾珠磨損、滾道磨損及絲杠彎曲4 種狀態試件，檢測每種試件運行時20 組振動信號。取出每種狀態前16 組作為訓練集，剩余4 組作為測試集。

3.2 特征提取

(1)時域特征:標準差、均方根、峭度、峰值、峰度、偏斜度。

(2)頻域特征:能量。依據EMD 方法適合于分析非線性、非平穩信號序列的特性［6-7］。本例借該法對采集的振動信號進行經驗模態分解，并提取前8 個本征模函數(IMF)的能量值C 作為頻域特征。

本實例分別提取X、Y、Z 三向振動信號的前8 個IMF 能量和6 個時域特征指標，總共42 類特征值。

3.3 特征篩選

3.3.1 BP 網絡設計

由于本例中MIV 依附于BP 網絡訓練進行篩選，這里首先需要對BP 網絡進行設計。

(1)輸入層:等于特征值個數為42;

(2)輸出層:利用1 個節點輸出值表示4 種故障狀態，期望輸出結果為:

正常為“1”、滾珠磨損為“2”、滾道磨損為“3”、絲杠彎曲為“4”;

(4)學習速率

通常情況下傾向于選取較小的學習速率以保證系統的穩定性。學習速率的選取范圍在0.01～0.8 之間［8］。結合本實驗進行多次對比分析，選取學習速率為0.1 可達較好效果。

(5)期望誤差

通常期望誤差設定值越小，網絡診斷精度越高，但若太小會使網絡訓練時間過長甚至不能收斂。經多次試驗，選取期望誤差為0.001 較為合適。

3.3.2 特征量篩選結果

依據MIV 算法得到各個特征的平均影響值(MIV)，依次填入表格并進行位次排序，見表1。由于表格格式限制，只列出排位前14 的特征值。

參照表1，選取與結果正相關且絕對值較大的前10 個特征作為新的特征集組合，按由大到小排序分別是:C1X、C1Z、C3X、峰度Y、C5Z、C2X、C1Y、標準差X、C2Y、標準差Y。

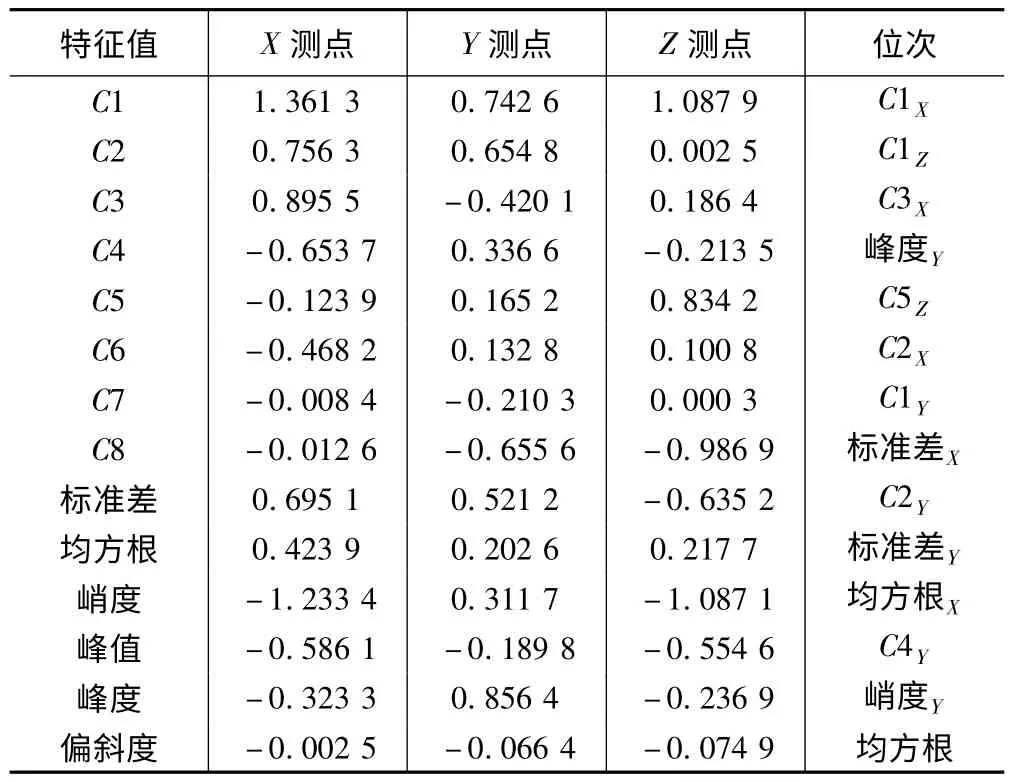
表1 平均影響值MIV

3.4 模式判別

3.4.1 建立RBF 神經網絡

調用Matlab 工具箱中newrb 函數實現對RBF 網絡進行的設計。newrb 函數格式如下:

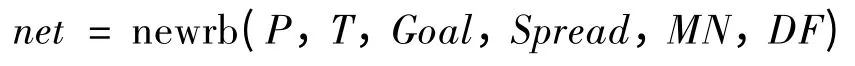
P 為輸入向量:對應經MIV 篩選后的10 類特征量。T 為目標向量:輸出層節點數，利用4 個節點輸出值表示4 種故障狀態，期望輸出結果為:正常［1，0，0，0］、滾珠磨損［0，1，0，0］、滾道磨損［0，0，1，0］、絲杠彎曲［0，0，0，1］。Goal 為均方誤差，本例取作0.001;Spread 為徑向基函數的分布密度，默認為1。MN 為神經元的最大數目。DF 為兩次顯示之間所添加的神經元數目，默認為1。

3.4.2 不同診斷模式對比分析

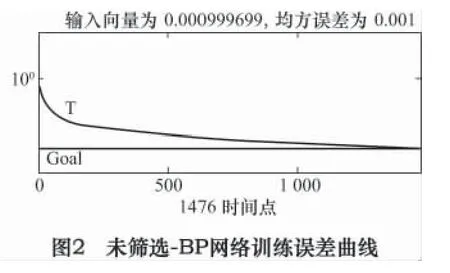
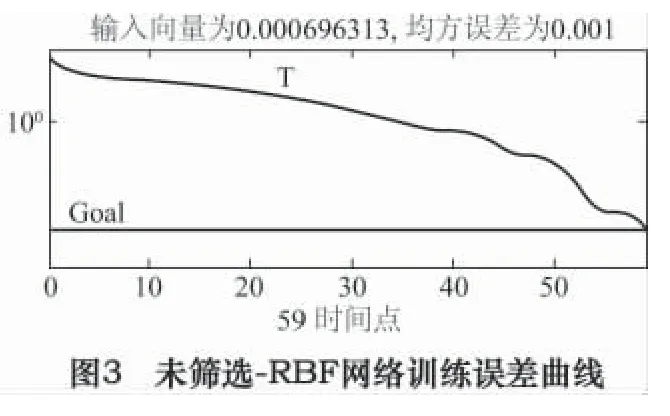
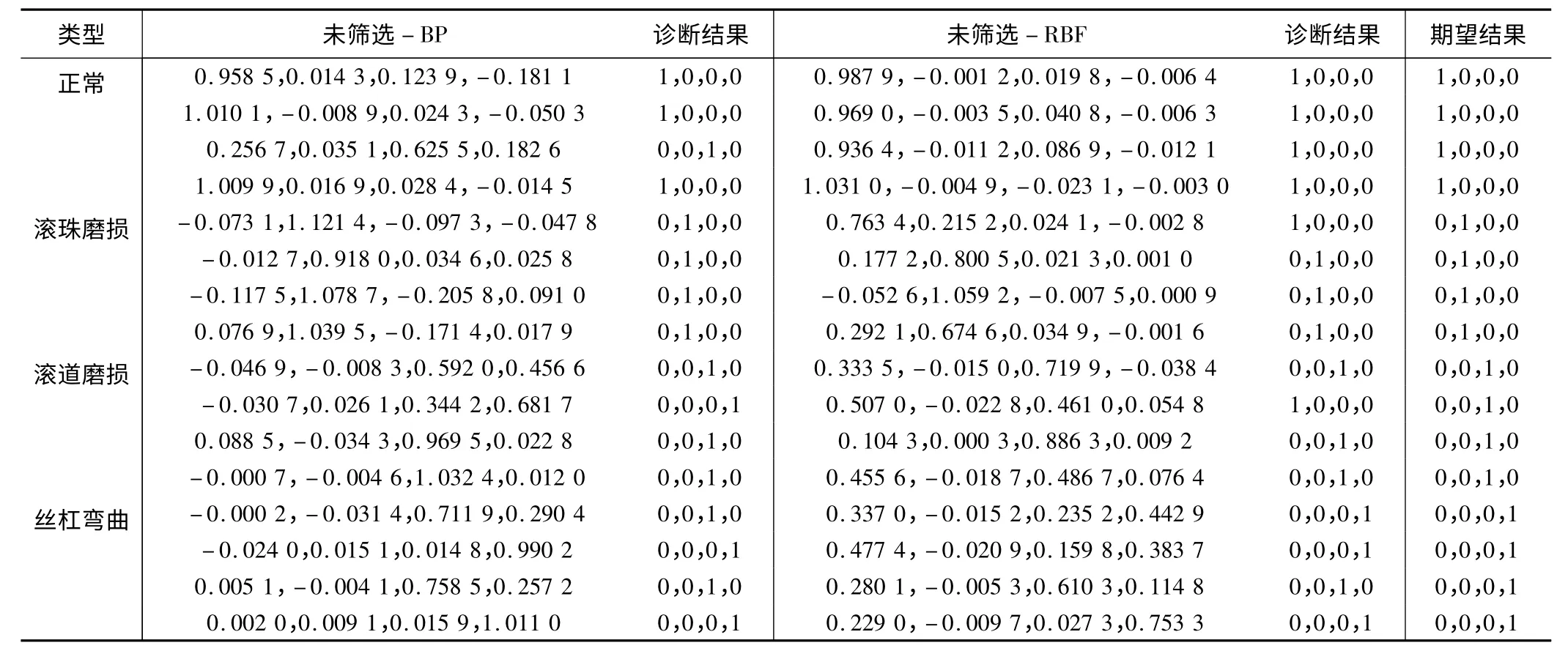
表2 未篩選-BP、未篩選-RBF 實際輸出及診斷結果

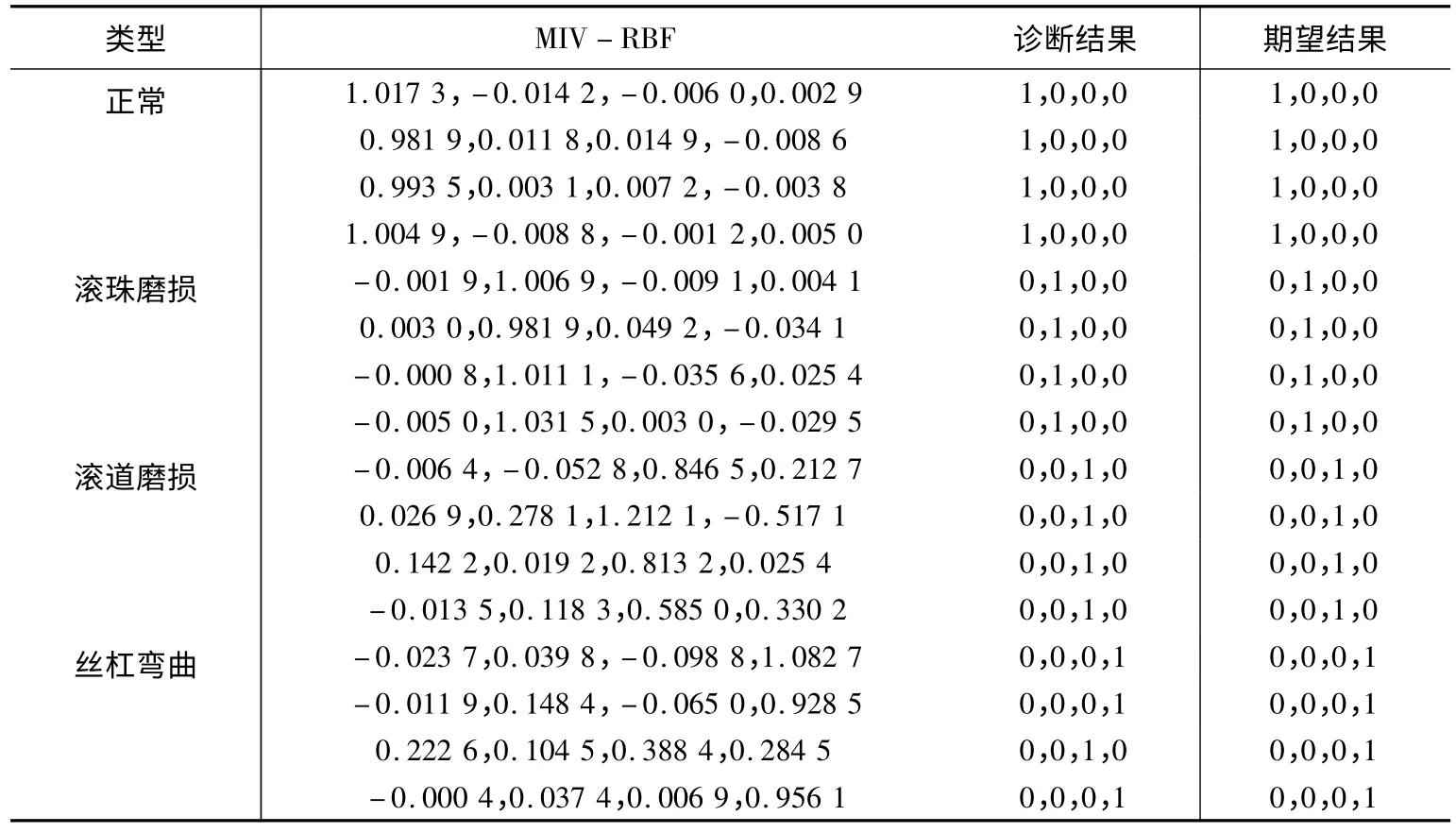
表3 MIV-RBF 實際輸出及診斷結果

對“未篩選-BP”、“未篩選-RBF”、“MIV -RBF”三種模式訓練與診斷結果進行分析，得到網絡訓練誤差曲線如圖2、圖3、圖4 所示;網絡實際輸出及診斷結果見表2、表3。

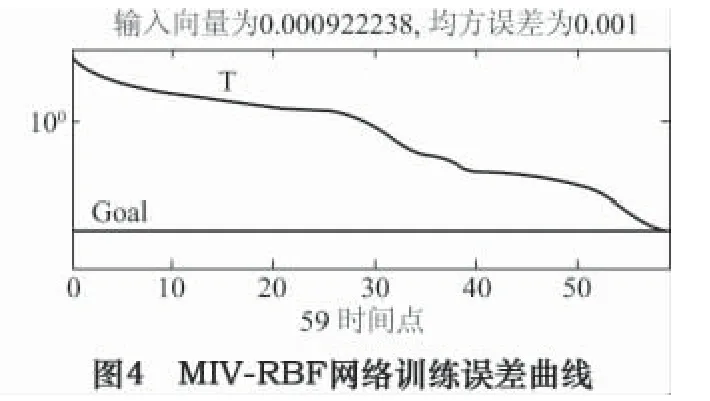
在BP 網絡、RBF 網絡的輸入層、隱含層、輸出層、期望誤差一致的情況下，通過對3 種診斷模式的訓練與診斷結果進行對比分析，得出結論匯總表，見表4。由表4 可得:

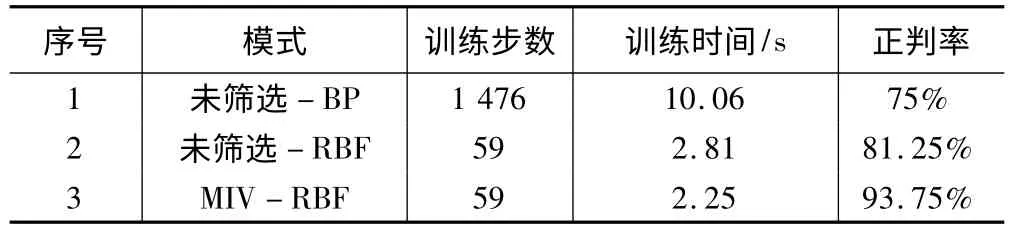
表4 匯總

(1)RBF 網絡相對于BP 網絡，能使用較少的訓練步數，在較短的訓練時間內達到收斂，完成訓練;同時具有較高的正判率。

(2)基于MIV 篩選后的RBF 網絡診斷相對于未篩選的RBF 網絡，訓練速度相差不大，但是正判率有明顯地提高。

4 結語

為了實現對滾珠絲杠的故障診斷，本文提出了一種基于MIV 與RBF 神經網絡的故障診斷方法。該方法首先通過MIV 算法對獲得的特征進行篩選處理，保留對診斷結果影響較大的特征構成新的特征集合。將新的特征集作為網絡輸入，構建RBF 神經網絡以實現診斷功能，并與傳統診斷方法進行比較，驗證了該方法在滾珠絲杠故障診斷中的可行性和優越性。

［1］王植，殷愛華.滾珠絲杠導程誤差分析與計算機輔助診斷研究［D］.南京理工大學，2004:1 -3.

［2］周瑩，程衛東.基于MIV 特征篩選和BP 神經網絡的滾動軸承故障診斷技術研究［D］.北京:北京交通大學，2011:25 -27.

［3］王紫微，葉奇旺.基于神經網絡MIV 值分析的腫瘤基因信息提取［J］.數學的實踐與認識，2011，41(14):47 -57.

［4］史峰，王小川，郁磊，等.MATLAB 神經網絡30 個案例分析［M］.北京:北京航空航天大學出版社，2010:65 -72.

［5］郭秀容，陸懷民.RBF 神經網絡在電噴發動機故障診斷中的應用研究［D］.哈爾濱:東北林業大學，2005:9 -12.

［6］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the hilbert spectrum for non -linear and non -stationary time series analysis［C］.Proc.R.Soc .Lond.A，1998，454:903 -995.

［7］Shen F，Zheng M，Shi D F，et al.Using the cross -correlation technique to extract modal parameters on response-only data［J］.Journal of Sound and Vibration，2003，259(5):1163 -1179.

［8］王凡重，田慕琴.基于小波神經網絡和支持向量機的電機故障診斷與研究［D］.太原:太原理工大學，2011:46 -47.