基于系統動力學的供應鏈融資零售商訂貨策略

馬中華， 孔偉

(上海海事大學 經濟管理學院，上海 201306)

0 引 言

企業資金約束已經成為制約供應鏈競爭力提高的關鍵，除直接的銀行信用融資外，實踐中還有兩種常見的融資方式：一是上游企業參與的貿易信用融資；二是第三方物流企業參與的存貨質押融資.貿易信用是以上游企業允許下游企業延遲支付貨款為主要方式，常見于供應鏈內有資金充裕或融資便利的企業的情況.存貨質押融資是企業將所持有的季節性存貨等抵押給銀行，由第三方物流企業負責監管，從而獲得銀行貸款的一種融資模式，對固定資產較少、信用度較低的中小企業更為適用.

貿易信用作為一種供應鏈內部融資渠道，在實踐中被廣泛采用，已經引起業界和學者的關注.ELLIEHAUSEN等[1]指出貿易信用融資在實踐中被幾乎所有類型的企業所采用，貿易信用(應付貨款)占非金融、非農業類小型企業總負債的20%，占所有大型企業總負債的15%；ATANASOVA等[2]指出大多數企業都同時既是貿易信用的提供者，又是貿易信用的需求者.存貨質押融資是在解決中小企業融資難題的實踐中發展起來的[3]，相應的理論研究也取得一定的成果.國外學者的研究成果主要集中于金融工具質押的融資定價問題，JOKIVUOLLE等[4]建立質押商品價值與企業違約概率相關條件下的風險債務模型，并給出經濟學解釋；COSSIN等[5]研究質押融資的風險定價問題.國內學者對存貨質押融資的研究主要集中在第三方物流企業的重要價值和地位[6-7]、浮動抵押融資[8]、供應鏈協調下的最優績效[9]以及存貨質押融資中的貸款價值比率[10-12].

在現實中，企業所采用的融資途徑可能不止一種，而運營策略的選擇又會受到融資成本等的交互影響，因此本文研究同時采用貿易信用和存貨質押融資的零售商的訂貨策略問題.考慮上游企業為零售商提供貿易信用融資，允許一定延遲期限支付貨款，同時零售商可以將因批量訂貨所產生的存貨質押給銀行從而獲得支持日常經營運作的資金，則追求收益最大化的零售商的訂貨決策既受到市場需求的限制，又受到貿易信用期限和存貨質押融資利率的影響.考慮到零售商決策背景的復雜性，本文擬采用系統動力學理論進行分析和計算機模擬.

系統動力學應用于供應鏈管理的研究中由來已久，在供應鏈設計、物流、資金流、信息流的協調和整合等方面的定性與定量分析研究中發揮著重要作用.FORRESTER[13-14]將計算機科學和反饋控制理論應用于社會、經濟等系統的研究中.楊陽等[15]采用系統動力學理論，從牛鞭效應、供應商生產率和庫存水平3個方面,分析供應鏈環境下第三方物流的引入對供應商管理庫存策略的動態影響，并進行計算機模擬.張力菠等[16]利用系統動力學的方法，從系統動態角度研究供應鏈環境下庫存控制的動力學特性.李旭[17]以系統動力學模型為框架, 提出以預測平均值和誤差標準差為基礎確定訂貨量的庫存控制策略，并以庫存服務水平和庫存成本為目標，對所提出的庫存策略中的政策性參數進行組合優化.針對供應鏈融資的系統動力學問題主要集中于定性分析.汪洋等[18]基于系統動力學理論的供應鏈系統物流資金供需機制，構建資金供需平衡的系統動力學流程圖和模型方程.王欣[19]建立影響供應鏈融資的因素指標體系，運用系統動力學方法對影響供應鏈融資的因素進行分析，建立各因素之間的因果關系模型及動力學流圖.

零售商的訂貨策略不僅影響零售商的收益，而且影響供應商甚至供應鏈整體的收益，因此零售商的訂貨策略一直是供應鏈管理理論研究的熱點，而現實中零售商由于資金短缺往往難以實現最優訂貨數量.本文考慮面臨資金約束的零售商在貿易信用(供應鏈內部融資)和存貨質押融資(供應鏈外部融資)下的最優訂貨策略.為充分考慮零售商訂貨系統的動態特征，采用系統動力學方法進行仿真分析，最終給出零售商訂貨策略參數的組合優化結果.

1 零售商策略分析

模型變量:rorder為訂購速率;q為訂購量;TR為庫存調節時間;IG為庫存偏差;IE為期望庫存;IA為實際庫存;IO為初始庫存;d為安全系數;S為需求標準差;x為市場需求;rs為銷售速率;Ft為總預測量;F1為預測量1;F2為預測量2;a為指數平滑系數;FC為本期市場需求預測值;FI為市場需求預測輸入值;FO為市場需求預測輸出值;i為資金的機會收益率;p為零售價格;r為存貨質押貸款利率;w為批發價格;M為延遲支付期限;T為銷售周期;h為單位庫存持有成本;Ia為平均庫存;Pd為每日利潤;Pa為平均利潤;Pt為總利潤;D為步長;Tsi為仿真時間.

背景假設：(1)考慮一個供應商和一個零售商所構成的供應鏈系統;(2)供應商和零售商雙方具有完全信息，了解所有的成本、參數和規則;(3)供應商和零售商都是風險中性的，以各自收益最大化為目標;(4)市場需求是隨機不確定的，即零售商可能面對各種復雜多變的市場環境;(5)零售商面臨資金約束時可以向銀行申請存貨質押融資或憑借供應商給予的貿易信用進行訂貨;(6)零售商對市場需求的預測有多種方法，在此選取最通用的一次指數平滑法進行預測.

1.1 零售商訂貨策略模型

零售商訂貨可認為是立即補貨(即庫存調節時間為1),且采取庫存偏差法向供應商訂貨，此種情況下零售商訂貨的基本系統動力學模型見圖1.

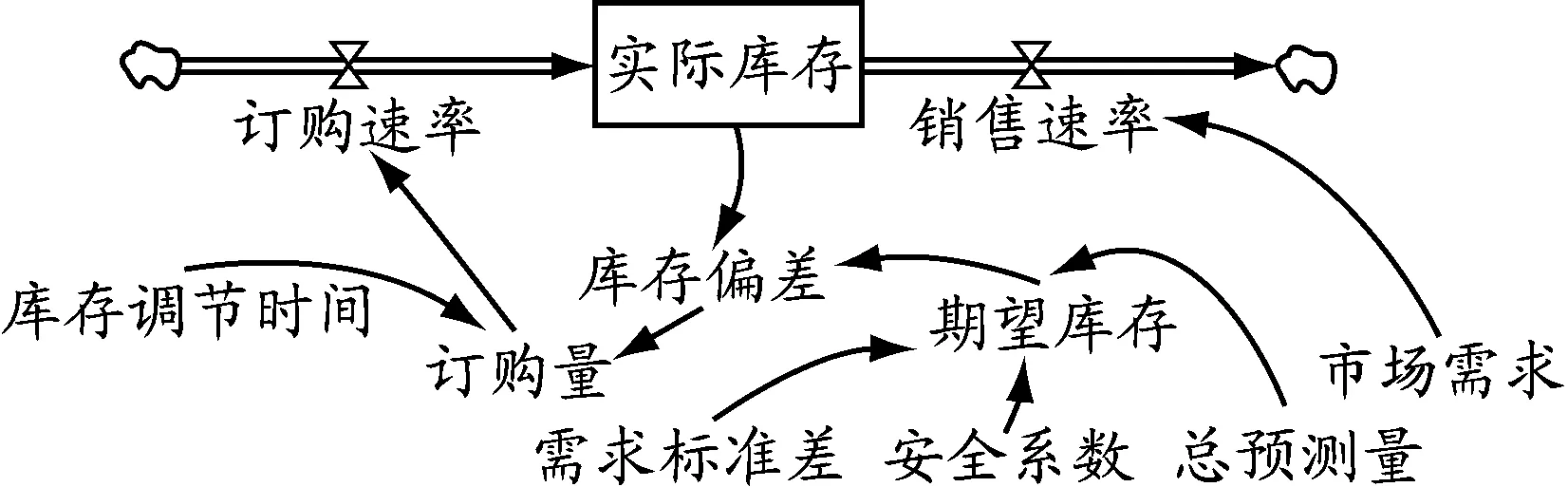
圖1 零售商訂貨的基本系統動力學模型

相關參數滿足:rorder=q;q=IG/TR;IG=IE-IA;IE=d·S+Ft;rs=x;IA=(INTEG(rs-rorder))·D+I0.式中:INTEG函數為積分函數，(INTEG(rs-rorder))·D為銷售速率與訂購速率之差在D時間段內的累積.期望庫存由安全庫存和市場需求的預測量組成，安全庫存可看成安全系數與需求標準差的乘積，庫存偏差為期望庫存與實際庫存的差值.

1.2 指數平滑法預測模型

本文采用指數平滑法預測市場需求，同時假定安全系數(服務水平)對市場需求也有影響，即高服務水平將增加未來的市場需求，其系統動力學模型見圖2.

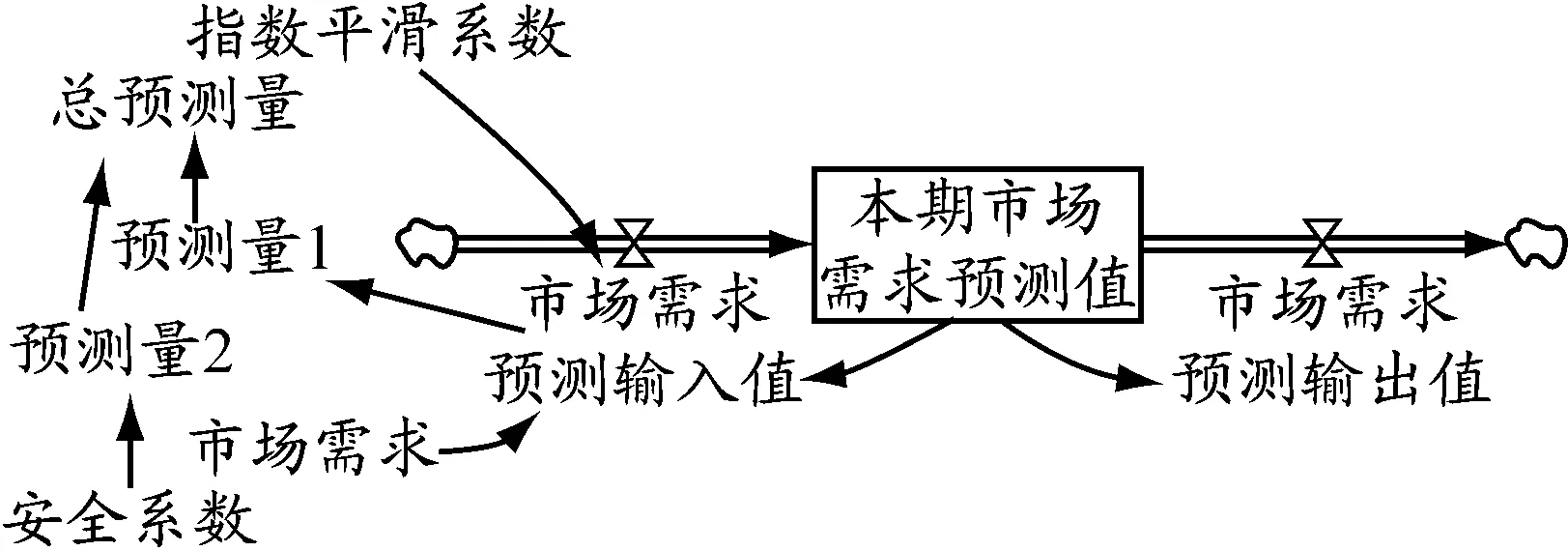
圖2 指數平滑法預測的系統動力學模型

相關參數滿足：FI=ax+(1-a)FC;FO=FC;F1=FI.安全系數d對需求預測量的影響可用表函數表示，根據歷史數據，設定F2=WITH LOOKUP(d)LOOKUP([(0,-8)-(10,10)],(0.84,-8),(1.04,-5),(1.28,0),(1.65,5),(1.96,7),(2.05,8)).其中表函數WITH LOOKUP可以建立兩個變量之間的非線性關系，其函數關系難以用具體的函數表示，只能通過輸入自變量與因變量的最大值和最小值以及一系列點加以控制.且零售商在銷售過程中的服務水平的提高會提高消費者的滿意度，吸引更多的客源，進而使市場需求量增大.最終的市場需求預測量由根據指數平滑法得到的預測量和安全系數對預測量的修正兩部分組成,即Ft=F1+F2.

1.3 零售商的控制目標

假設零售商沒有初始資金，供應商為刺激零售商多訂貨允許零售商延遲支付貨款，期限為M，零售商需要在M內用銷售收入償還供應商的貨款.延遲支付期限時間M小于訂貨周期T，需求量在訂貨周期內與時間成正比.

市場需求是隨機的，根據實際中可能的情況分為4類:(1)市場需求很大，在M內零售商可以用銷售收入償還供應商的貨款，零售商在延遲支付期限結束后，繼續銷售商品，周期末無剩余貨物.(2)市場需求較大，在M內零售商可以用銷售收入償還供應商的貨款，零售商在延遲支付期限結束后，繼續銷售商品，周期末將剩余貨物按殘值處理.(3)市場需求較小，在M內零售商不能用銷售收入償還供應商的貨款，零售商在延遲支付期限結束后，將剩余貨物抵押給銀行，申請存貨質押貸款，由銀行支付所欠供應商貨款，到期末零售商的銷售收入可以償還銀行的借款本息，剩余貨物歸零售商所有.(4)市場需求很小，在M內零售商不能用銷售收入償還供應商的貨款，零售商在延遲支付期限結束后，將剩余貨物抵押給銀行，申請存貨質押貸款，由銀行支付所欠供應商貨款，到周期末零售商的銷售收入不能償還銀行的借款本息，剩余貨物歸銀行所有，此時可認為零售商的利潤為零.

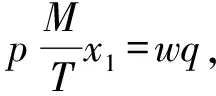
將零售商在整個時間段內的平均利潤最大化作為控制目標，描述這項指標的系統動力學協流結構見圖3.

描述利潤的系統動力學方程為

Pa=Pt/Tsi

Ia=q/2+drs

式中:平均利潤為總利潤與仿真時間的比值；平均庫存為經常性庫存與安全庫存之和.為分類討論不同市場需求下零售商每天的利潤，采用Vensim的IF THEN ELSE函數.

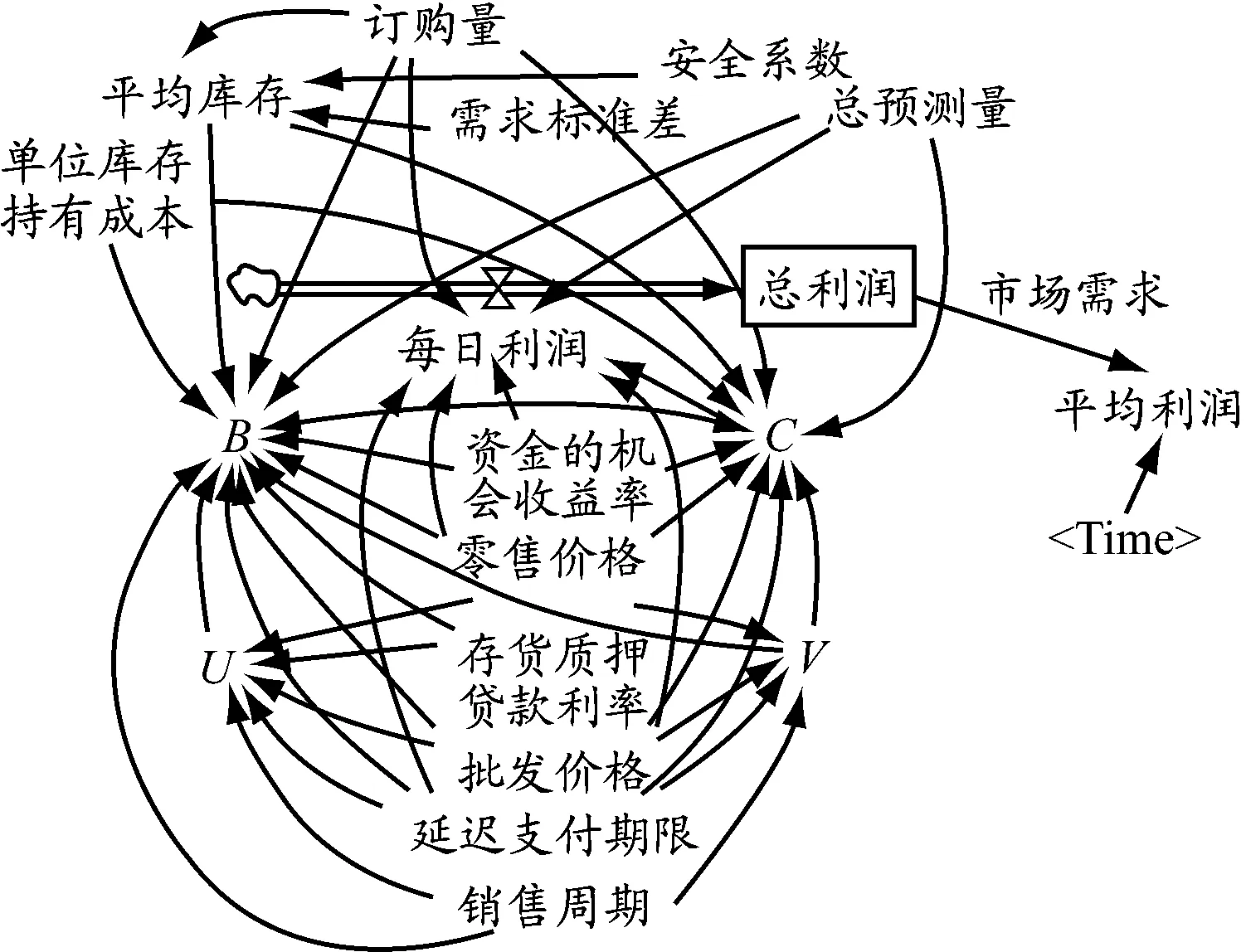
圖3 零售商平均利潤最大的協流結構

(1)Ft≥q時，零售商的收益為pq+iwqM，成本為wq.

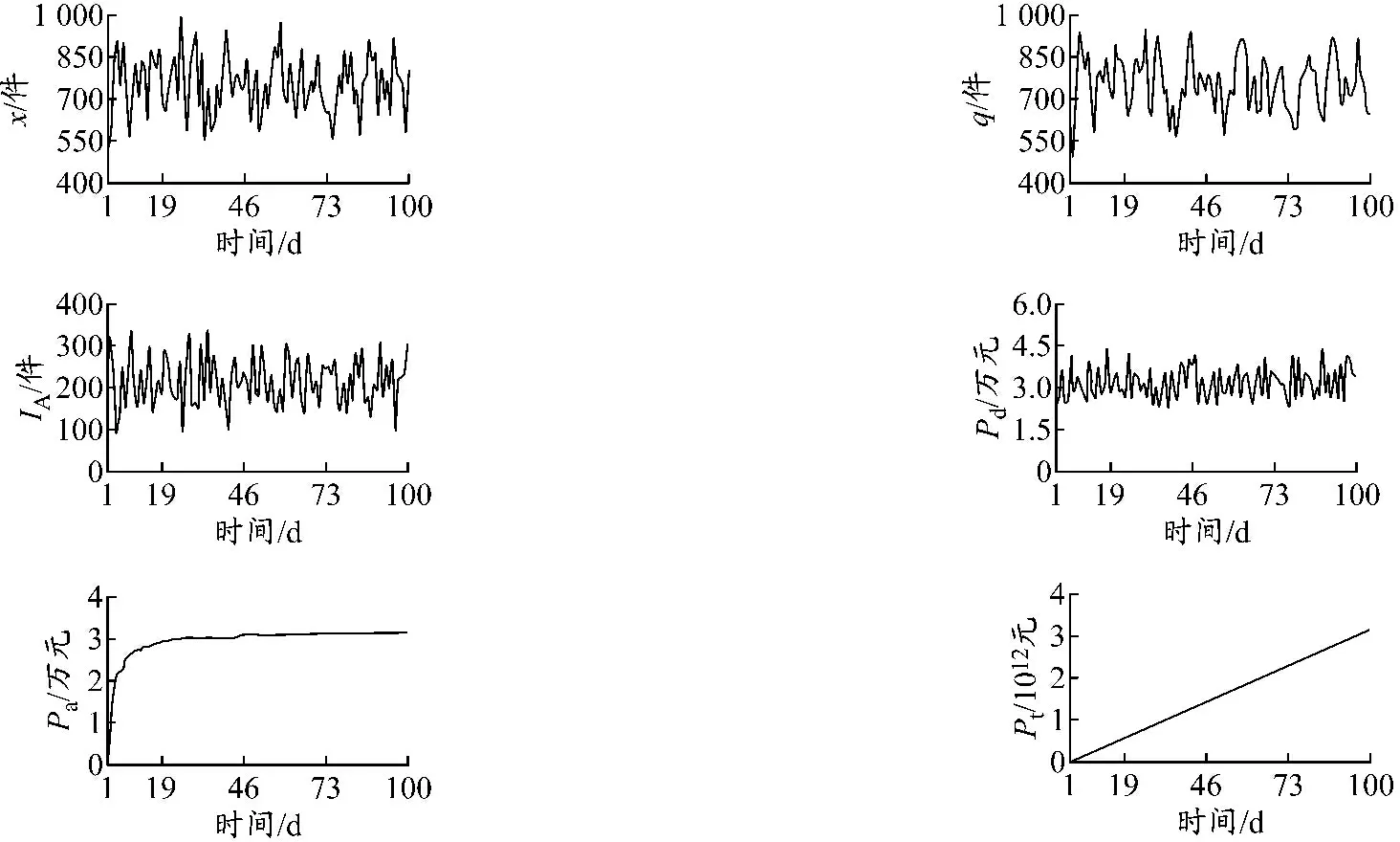
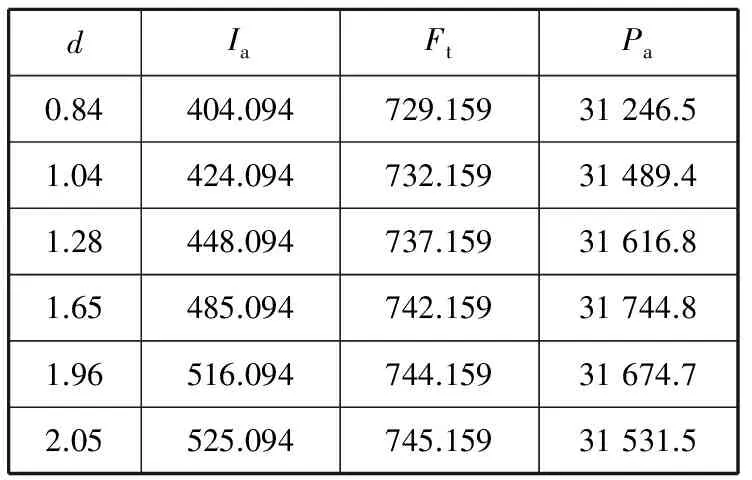
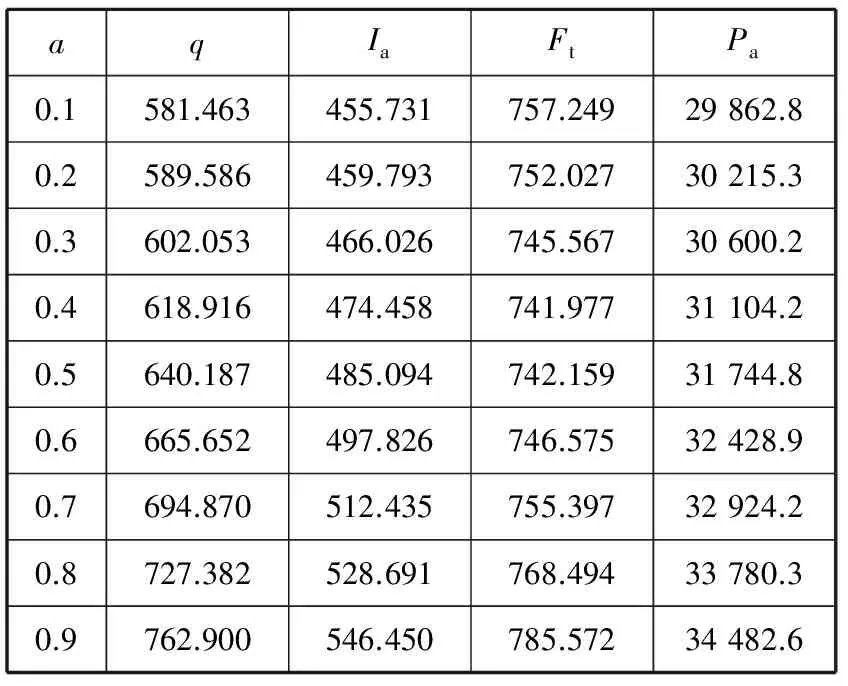
(2)Uq≤Ft

(3)Vq≤Ft

相關系統動力學方程為

Pd=IF THEN ELSE(Ft≥q,pq+iwqM-wq,B)

B=IF THEN ELSE(Uq≤Ft:AND:Ft

iwqM-wq-Iah,C)

C=IF THEN ELSE(Vq≤Ft:AND:Ft

iwqM-pMFt/T+(wq-pMFt/T)(1+

r(T-M))-Iah,0)

2 系統仿真與參數優化

考慮某服裝零售商的訂購策略.p=100元/件，w=50元/件，h=20元/件，T=90天；供應商提供的M=60天.x服從(750,1002)的正態分布.r=0.002元/(d·元)，供應商提供給零售商的i=0.001元/(d·元).初始需求預測值為均值750件，初始庫存水平為200個，初始利潤為0.以d為單位，仿真區間為1～100 d.取d=1.28,a=0.5，仿真結果見圖4.

從仿真結果可以看出：(1)零售商的q與x的變化方向基本相同，IA與x的變化方向呈現相反的趨勢，且都存在一定的滯后.零售商根據本時刻的x確定下一時刻的x預測量，進而根據IG確定下一時刻的q.本時刻x的實際值越大，零售商為防止缺貨損失，下一時刻的q將會越大，同時IA因商品售出而降低.(2)零售商的Pd會呈現周期性波動，Pt會隨時間呈直線上升的趨勢，但Pa會有先上升后趨于平穩的趨勢.這是因為x每天都是不確定的，零售商的Pd會出現較大的波動.由于管理者根據某種規則或經驗對系統實施管理和控制，幾經周折發現系統運行的內在規律后，系統逐漸達到穩定狀態.顯然，Pt隨著時間的積累會呈現一直上升的趨勢.

圖4d=1.28,a=0.5時的仿真結果

本文考慮零售商在供應鏈融資下的訂貨策略，d和a分別用于確定零售商的現貨供應水平和未來需求的預測量，是零售商的決策變量.下面采用政策研究的試湊法以平均利潤最大化為目標對d和a進行組合優化.

2.1 安全系數敏感性分析

考察a不變時d的變化對零售商Ia,Ft和Pa的影響.考慮到通常情況下零售商提供的服務水平取值范圍，選取與服務水平從80%到98%所對應的d(0.84到2.05)作為d的變化范圍.為更好地定量研究各類指標，將最后時刻各變量值輸出，見表1.

表1 d的敏感性分析

從表1中可以看出，隨著d的增大，零售商的Ia和Ft都有上升的趨勢，Pa呈現先上升后下降的趨勢，并在d=1.65時達到最大值.這是由于零售商為達到更高的服務水平，必然增大安全庫存，同時更高的服務水平又會使市場需求增大，使銷售收入提高.當提高的銷售收入大于增加的庫存持有成本時，零售商的Pa增大，否則，Pa會下降.為此，取d=1.65，即服務水平為95%，使零售商平均利潤最大化.

2.2 平滑系數敏感性分析

考察d不變時a的變化對零售商Ia,Ft和Pa的影響.固定d=1.65，a的變化范圍為0.1～0.9.同樣，為更好地定量研究各類指標，將最后時刻各變量值輸出，見表2.

表2 a的敏感性分析

從表2可以看出，隨著a的增大，零售商的q和Ia有上升的趨勢，Ft呈現先下降后上升的趨勢，零售商的Pa呈現上升的趨勢.這是因為當市場需求呈現明顯且迅速的上升或下降趨勢時，選擇較大的a使預測模型靈敏度較高，才能迅速跟上數據的變化.在此例中零售商的q一直小于Ft，由a的增大所導致的銷售收入的增加量一直大于增加的庫存持有成本，Pa會呈現一直增加的趨勢.當a=0.9時，Pa達到最大值.為此，取a=0.9.

通過敏感性分析以及政策參數優化的試湊法，可以得到當d=1.65，a=0.9時，面臨資金約束的零售商可以在模擬的時間段內實現Pa最大化，此時Pa為34 482.6元.

3 結束語

采用系統動力學對供應鏈融資的零售商運營策略進行建模，考慮同時采用貿易信用和存貨質押融資兩種融資模式下，面臨資金約束的零售商收益最大化的訂購策略.模型中采用指數平滑方法對市場需求進行預測，并對零售商的訂購策略進行多個周期的模擬，對零售商訂貨策略的相關參數進行靈敏度分析.采用試湊法對策略參數進行優化，最終確定零售商訂貨策略的最優安全系數和指數平滑系數.

為分析貿易信用和存貨質押融資下零售商的訂貨策略優化問題，僅考慮單一零售商和單一供應商所構成的簡單供應鏈，同時假定批發價格、零售價格等參數固定不變，沒有考慮實際中可能遇到的與訂購批量相關的價格折扣、產品促銷等更為復雜的情況，以及多個供應商和多個零售商構成的供應鏈網絡中存在的類似問題.同時，在仿真分析中，本文采用系統動力學方法給出供應鏈融資下實現零售商的最優訂貨策略中的安全系數和指數平滑系數的優化結果.由于仿真方法的局限性，不能實現兩個系數的同時優化，這在未來的研究中值得進一步探討.

參考文獻：

[1]ELLIEHAUSEN G, WOLKEN J. The demand for trade credit: an investigation of motives for trade credit use by small businesses[R]. Washington：Board of Governors of Federal Reserve System, 1993: 1-18.

[2]ATANASOVA C V, WILSON N. Bank borrowing constraints and the demand for trade credit: evidence from panel data[J]. Managerial & Decision Economics, 2003, 24(6/7): 503-514.

[3]陳祥鋒, 朱道立. 現代物流融資服務創新——金融物流[J]. 物流技術, 2005, 3(4/6): 15.

[4]JOKIVUOLLE E, PEURA S. Incorporating collateral value uncertainty in loss given default estimates and loan-to-value ratios[J]. European Financial Management, 2003, 9(3): 299-314.

[5]COSSIN D, HRICKO T. A structural analysis of credit risk with risky collateral: a methodology for haircut determination[J]. Economic Notes, 2003, 32(2): 243-282.

[6]陳祥鋒, 朱道立. 資金約束供應鏈中物流提供商的系統價值研究[J]. 系統工程學報, 2008, 23(6): 667-674.

[7]馬中華, 朱道立. 物流企業在存貨質押融資中的決策問題研究[J]. 系統工程學報, 2011, 26(3): 346-351.

[8]陳倫倫. 浮動抵押在造船抵押融資中的適用[J]. 上海海事大學學報, 2009, 30(1): 89-94.

[9]朱衛平, 劉偉, 高志軍. 三級物流服務供應鏈能力協調[J]. 上海海事大學學報, 2012, 33(2): 26-32.

[10]李毅學, 徐渝, 馮耕中, 等. 重隨機泊松違約概率下庫存商品融資業務貸款價值比率研究[J]. 中國管理科學, 2007, 15(1): 21-26.

[11]李毅學, 汪壽陽, 馮耕中. 物流金融中季節性存貨質押融資融資質押率決策[J]. 管理科學學報, 2011, 14(11): 19-32.

[12]嚴飛, 汪傳旭. 海陸倉融資模式下船公司質押率優化[J]. 上海海事大學學報, 2010, 31(1): 47-55.

[13]FORRESTER J W. Industrial dynamics[M]. US: MIT Press, 1961: 1-11.

[14]FORRESTER J W. World dynamics[M]. US: MIT Press, 1971: 1-18.

[15]楊陽, 劉志學. 供應商管理庫存與第三方物流的系統動力學模型[J]. 系統工程, 2007, 25(7): 38-44.

[16]張力菠, 韓玉啟, 陳杰, 等. 供應鏈管理的系統動力學研究綜述[J]. 系統工程, 2005, 23(6): 8-15.

[17]李旭. 二級供應鏈系統庫存策略的系統動力學研究[J]. 系統工程, 2009, 27(5): 1-6.

[18]汪洋, 郝紅雨. 基于系統動力學的供應鏈物流資金供求平衡[J]. 工業工程, 2009, 12(1): 46-50.

[19]王欣. 基于系統動力學的供應鏈融資模式研究[D]. 沈陽: 沈陽大學, 2011.