固化促進劑種類對集成電路封裝材料固化行為的影響

李 光，楊明山＊，張 卓，馮徐根，金洪廣

（1.北京化工大學材料科學與工程學院，北京100029；2.北京石油化工學院材料科學與工程學院，特種彈性體復合材料北京市重點實驗室，北京102617）

0 前言

隨著微電子技術以及集成電路封裝技術的發展，環氧模塑料（EMC）作為電子封裝關鍵材料，得到了快速的發展。EMC 的主要成分為環氧樹脂、固化劑、固化促進劑和填料等。其中，固化劑起交聯的作用，環氧樹脂只有在固化劑存在的條件下才可能打開環氧鍵，形成穩定的三維網狀結構。環氧樹脂與大部分固化劑反應都需要在較高溫度下才能發生固化交聯，為了降低固化反應溫度、縮短固化反應時間，需要在EMC 中加入固化促進劑，固化促進劑主要有胺類、咪唑類、膦類［1－3］。由于各自分子結構及催化活性的差異，不同種類的固化促進劑對集成電路封裝用EMC 固化的促進效果、封裝工藝和固化后的性能具有重要的影響。本文采用非等溫DSC 法對EMC 的固化行為進行了研究，為其配方優化和集成電路封裝工藝的確定提供基礎數據。

1 實驗部分

1.1 主要原料

鄰甲酚醛環氧樹脂，JEN－801，江山江環化學工業有限公司；

溴化環氧樹脂，EB－400，江山江環化學工業有限公司；

酚醛樹脂，A002－34，連云港市中和科技有限公司；

三氧化二銻，天津市福晨化學試劑廠；

硅微粉，DRG－600，連云港東海硅微粉有限責任公司；

硅烷偶聯劑，WD－60，武漢武大有機硅材料有限公司；

巴蠟，巴蠟1號，市售；

2－甲基咪唑、三苯基磷，廣州市固研電子材料有限公司。

1.2 主要設備及儀器

高速混合機，SHR10B，張家港市輕工機械有限公司；

雙輥開煉機，IR502，東莞市臺銳儀器有限公司；

動態差示掃描量熱儀（DSC），DSC－60，日本島津公司；

1.3 樣品制備

分別按照鄰甲酚醛環氧樹脂16份（質量份，下同）、溴化環氧樹脂2份、三氧化二銻1份、酚醛樹脂6.5份、硅微粉72份、硅烷偶聯劑0.8份、巴蠟1號0.8份、配方1選用2－甲基咪唑0.1份、配方2選用三苯基磷0.1份準確稱量各組分，放入高速混合機中，高速混合20s，靜置1min，連續混合3次；后采用雙輥開煉機進行混煉，溫度90～100 ℃，開煉時間3～5min，輥速前后比為1.0∶1.2；雙輥開煉后冷卻，經過粗粉碎、細粉碎，然后過孔徑為150μm 的網篩，進行測試。

1.4 性能測試與結構表征

非等溫固化行為測試：氮氣氣氛，氣體流量為50mL／min，稱取3～5mg待固化樣品于鋁坩堝中，壓蓋，用空白鋁坩堝作參比，溫度范圍30～250 ℃，升溫速率分別為5、10、15、20 ℃／min，得到樣品DSC曲線。

2 結果與討論

2.1 實驗原理

EMC固化反應為放熱反應，在DSC曲線上會出現固化放熱峰，該放熱峰的起始溫度Ti、峰值溫度Tp和終止溫度Te隨升溫速率的增大逐漸向高溫方向移動。這主要是因為升溫速率增大，d H／dt增大，即單位時間內放出的熱量多，產生的溫差大，表現為放熱峰向高溫移動。

用非等溫DSC 分析環氧樹脂模塑料的固化動力學，可采用Kissinger法、Crane法和Ozawa法。利用不同升溫速率下固化峰的峰值溫度Tp，就可以對固化動力學參數進行計算。

Kissinger［4］法是進行固化動力學處理時常采用的方法。Kissinger方程中，峰值溫度與升溫速率的關系為：

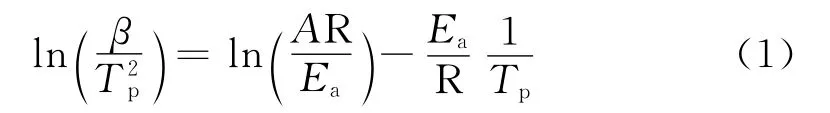
式中 β——升溫速率常數，值為dT／dt，℃／min

Tp——DSC曲線上放熱峰的峰值，K

A——指前因子

R——理想氣體常數，值為8.314J／（mol·K）

Ea——固化活化能，J／mol

反應級數是反應復雜與否的宏觀表征，通過反應級數的計算可簡單地判定反應過程的復雜程度，及粗略地估計固化反應機理。反應級數n 可用Crane［5］方程計算：

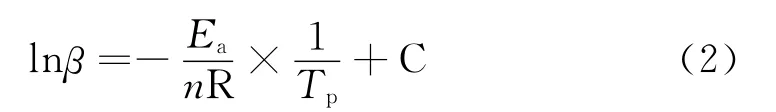
式中 C——常數

n——反應級數

以－lnβ對1／Tp作圖，通過線性擬合可得直線斜率Ea／nR，將Kissinger法計算出的活化能Ea帶入，進而可求得固化反應級數n。

固化反應的活化能也可由Ozawa［6］方程得到：

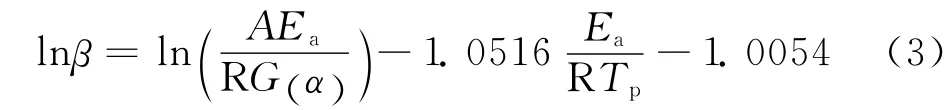
式中 G（α）——與轉化率有關的函數

以－lnβ 對1／Tp作 圖，經 擬 合 得 直 線 斜 率1.0516Ea／R，由此可計算出固化活化能Ea。

2.2 不同固化促進劑種類EMC的固化活化能

圖1為2－甲基咪唑、三苯基磷2個體系在不同升溫速率下的DSC 曲線。可以看出，2種體系的放熱曲線隨升溫速率的不同而不同，DSC 曲線上均只出現一個放熱峰。在同一體系中，隨著升溫速率的增大，固化反應的起始溫度（Ti）、峰值溫度（Tp）和終止溫度（Te）都會升高。對比2種體系的DSC 曲線可以看出，以三苯基磷為固化促進劑的體系有較高的Ti和較低的Te，其放熱峰的溫度區間跨度小于以2－甲基咪唑為固化促進劑的體系。

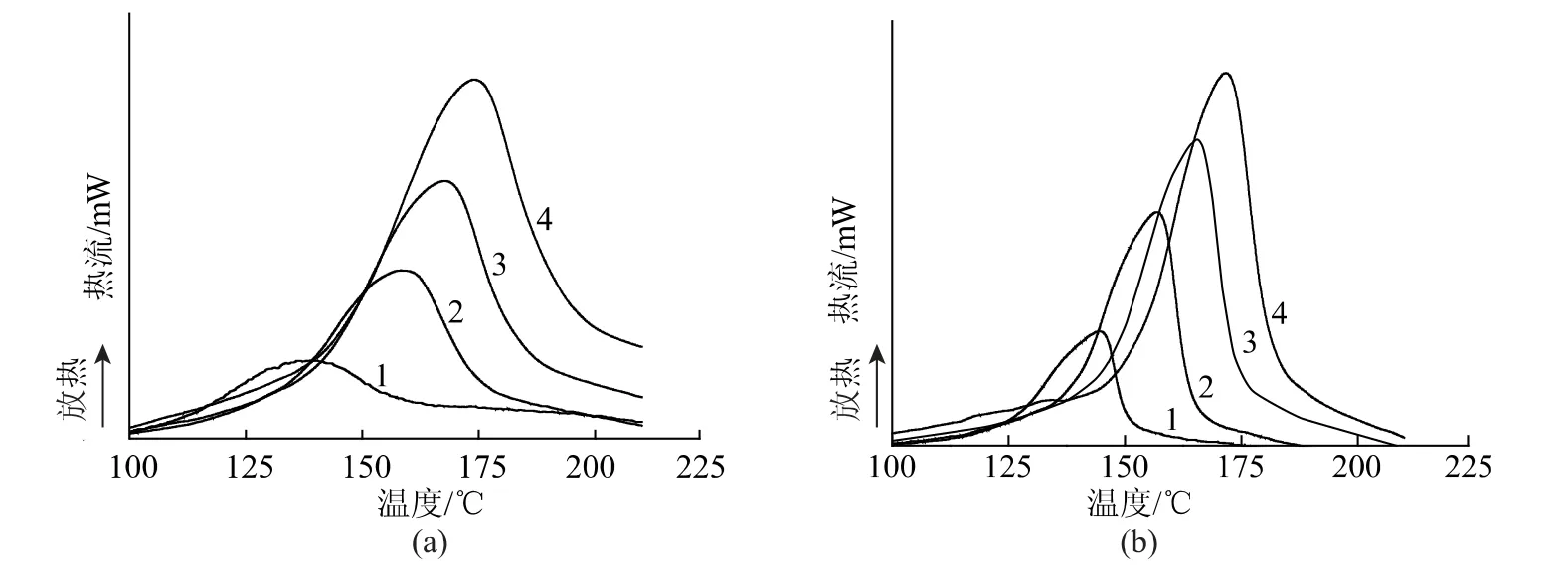
圖1 不同固化體系在不同升溫速率下的DSC曲線Fig.1 DSC curves of two curing stytems at different heating rate

2.2.1 Kissinger法計算固化活化能

根據DSC實驗數據，以ln（T2p／β）對1／RTp作圖，見圖2，通過線性擬合計算直線斜率K，可求得固化活化能Ea。從 圖2 擬 合 直 線 可 以 看 出，ln（T2p／β）與1／RTp有良好的線性關系，由直線斜率得體系固化活化能Ea。2－甲基咪唑體系的固化活化能為63.821kJ／mol，三 苯 基 磷 體 系 的 固 化 活 化 能 為71.562kJ／mol。

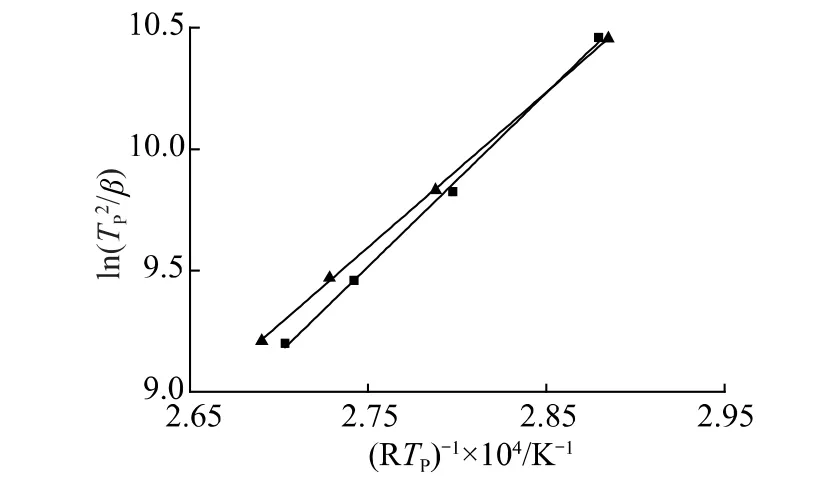
圖2 不同固化體系的ln（T／β）與1／RTp 擬合直線Fig.2 Curves of ln（T／β）－1／RTpof two curing systems

通過對比不同固化促進劑種類對環氧模塑料固化行為的影響，發現以2－甲基咪唑為固化促進劑的體系，其反應的活化能小于以三苯基磷為固化促進劑的體系，這就表明其更容易發生反應，該體系性能優于三苯基磷固化體系。

2.2.2 Ozawa法計算固化活化能

根據DSC數據，以－lnβ對1／Tp作圖，見圖3，經擬合得直線斜率1.0516 Ea／R，由此可計算出固化活化能Ea。2－甲基咪唑體系的固化活化能為67.507kJ／mol，三苯基磷體系的固化活化能為74.861kJ／mol。

通過Ozawa法計算出固化活化能的結果與Kissinger法計算固化活化能的結果相比較，數值上有些許不同，但整體范圍和趨勢不變，即固化促進劑為2－甲基咪唑的體系其固化活化能較低。

以Kissinger法和Ozawa法所得活化能的平均值為各固化體系的活化能，2－甲基咪唑體系的活化能為65.664 kJ／mol，三 苯 基 磷 體 系 的 活 化 能 為73.211kJ／mol。

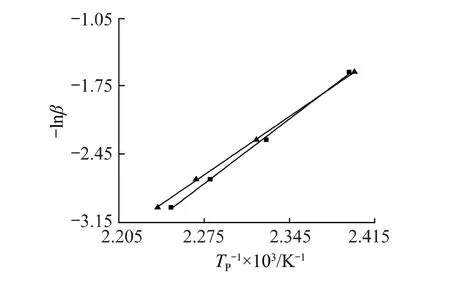
圖3 不同固化體系的－ln（β）與1／Tp 擬合直線Fig.3 Curves of－ln（β）－1／Tpof two curing systems

2.2.3 Crane法計算反應級數

根據DSC數據，以－lnβ對1／Tp作圖，見圖3。通過線性擬合可得直線斜率Ea／nR，將Kissinger法計算出的活化能Ea帶入，進而可求得固化反應級數n。

2－甲基咪唑體系的反應級數為1.028，三苯基磷體系的反應級數為1.059。2 種固化體系的反應級數比較接近，在簡化處理的前提下其固化反應都接近于一級反應，由此可以看出，固化促進劑種類對反應級數影響很小。

2.2.4 n級動力學模型

環氧樹脂體系固化反應的動力學研究大多采用唯象模型中的n級動力學模型：

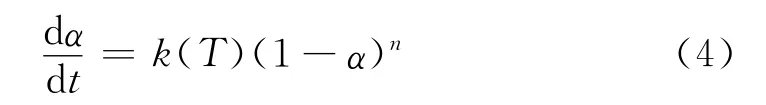
式中 dα／dt——反應速率

α——固化度

k（T）——反應速率常數，與溫度相關

根據Arrhenius方程：

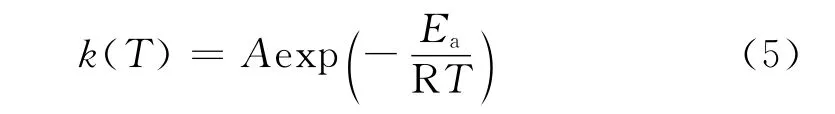
式（4）可改寫為：

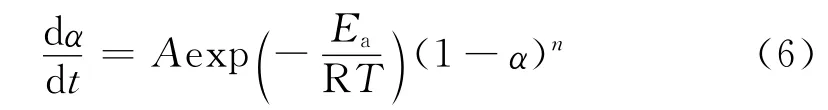
結合前面求出的動力學參數Ea、n，可得出固化體系的n級固化動力學模型方程。

2－甲基咪唑體系的固化動力學方程為：

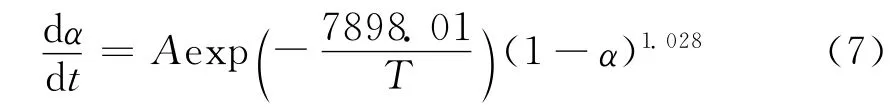
三苯基磷體系的固化動力學方程為：

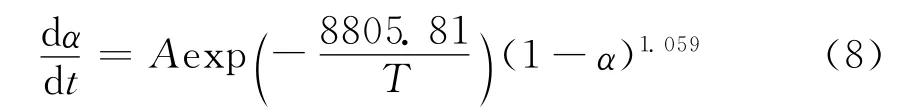
該模型可以為EMC 工藝參數的選擇提供必要的理論依據。

2.3 固化工藝的確定

EMC在一定固化工藝下進行固化反應，其固化程度對性能有較大影響。固化程度越高，熱性能越好。不同升溫速率下的體系起始溫度（Ti）、峰值溫度（Tp）和終止溫度（Te），對不同升溫速率下的3個溫度值進行線性回歸，外推得到升溫速率為零時的固化起始溫度、峰值溫度和終止溫度，從而可以確定環氧樹脂模塑料的最佳固化溫度范圍，初步確定固化工藝。

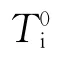
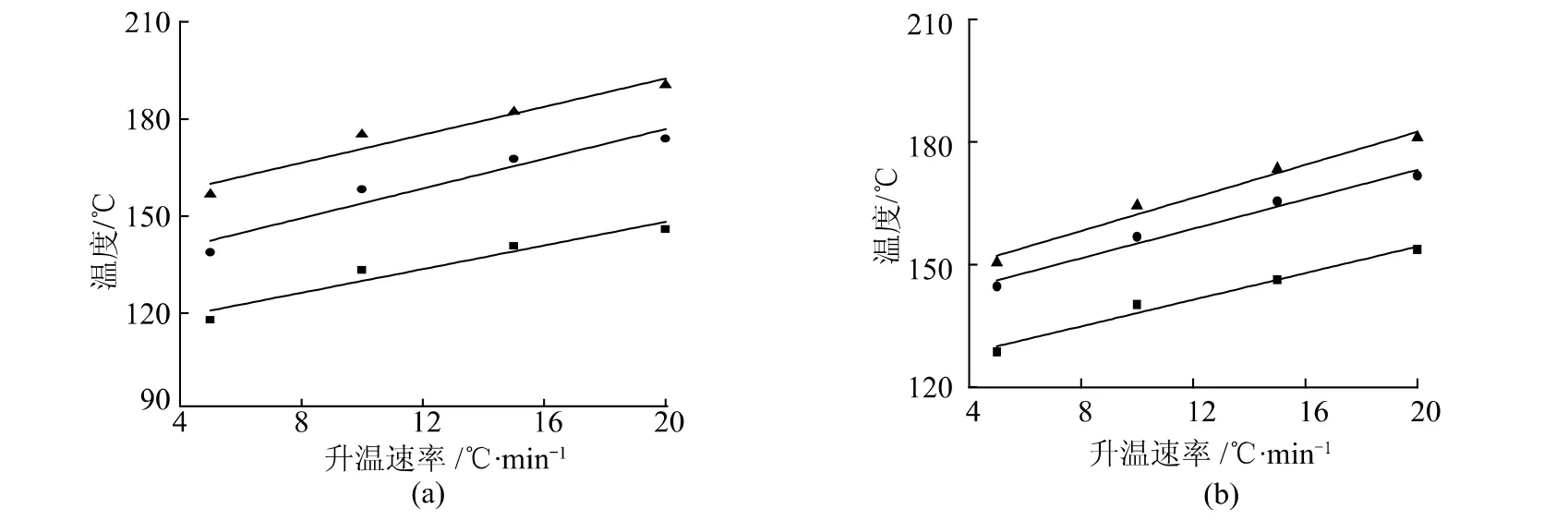
圖4 Ti、Tp和Te與升溫速率的關系曲線Fig.4 Curves of curing temperature vs incresing rate of temperature

表1 環氧模塑料的動力學參數和固化工藝參數Tab.1 The kinetic parameters and curing parameters of EMCs

3 結論

（1）對不同固化促進劑種類的EMC 的固化行為進行了非等溫DSC分析，應用Kissinger、Crane和Ozawa方法獲得了反應活化能Ea、反應級數n 等固化動力學參數；其中，2－甲基咪唑體系活化能為63.821kJ／mol（Kissinger法）和67.507kJ／mol（Ozawa法），反應級數為1.028；三苯基磷體系活化能為71.562kJ／mol（Kissinger法）和74.861kJ／mol（Ozawa法），反應級數為1.059；

（2）推導出2－甲基咪唑體系固化反應過程的Ti0、Tp0、Te0分別為111.720、130.995、149.145 ℃；三苯基磷體 系 的Ti0、Tp0和Te0分 別 為121.790、137.090、142.035 ℃；

（3）固化促進劑為2－甲基咪唑的體系其固化活化能低于三苯基磷體系，該體系固化反應易于發生。

［1］ 韓江龍.環氧塑封料現狀及發展趨勢［J］.電子工業專用設備，2012，12：6－9.Han Jianglong.Current Situation and Development Trend of Epoxy Molding Compounds［J］.Equipment for Electronics Products Manufacturing，2012，12：6－9.

［2］ 孫曼靈.環氧樹脂應用原理與技術［M］.北京：機械工業出版社，2002：442－473.Sun Manling.Epoxy Resin Application Principle and Technology［M］.Beijing：Mechanical Industry Press，2002：442－473.

［3］ 亢雅君，殷立新.環氧樹脂中溫固化促進劑評述［J］.熱固性樹脂，1995，（2）：47－51.Kang Yajun，Yin Lixin.Review on Accelerators for Epoxy Resin under Middle Temperature［J］.Thermosetting Resin，1995，（2）：47－51.

［4］ Kissinger H E.Reaction Kinetics in Differential Thermal Analysis［J］.Analytical Chemistry，1957，29（11）：1702－1706.

［5］ Crane L W，Dynes P J，Kaelble D H.Analysis of Curing Kinetics in Polymer Composites［J］.Polymer Letter Edition，1973，11（8）：533－540.

［6］ Ozawa T.Kinetic Analysis of Derivative Curves in Thermal Analysis［J］.Journal Thermal Anal，1970，2：301－324.