基于CUDA的遙感圖像快速超分辨率重建算法研究

陳 昕 胡 杰 李 映

(西北工業大學 西安 710129)

0 引言

圖像超分辨率重建技術的基本思想是采用信號處理的方法，在改善圖像質量的同時，重建成像系統截止頻率之外的信息，從而在不改變硬件設備的前提下，獲取高于成像系統空間分辨率的圖像。如圖1所示，由于成像系統中存在不同的降質過程［1］，理想的高分辨率圖像x在成像過程中會受到形變、模糊(包括光學、傳感器和幀內運動模糊)、抽樣和噪聲等因素的影響，造成圖像質量的下降。實際應用中，對同一場景的多次成像會得到k幀低分辨率圖像:

式中，M(k)為第k幀低分辨率圖像成像過程中由運動引起的形變矩陣;B(k)為點擴散函數或衍射極限引起的模糊矩陣;D為下采樣矩陣，反映了成像系統對原始高分辨率場景的下采樣過程;n(k)為噪聲，通常被認為是加性高斯白噪聲。

從圖1 可以看出，圖像的超分辨率重建過程就是根據獲取的一幀或多幀低分辨率圖像y(k{)} 重建理想的高分辨率圖像x的過程，即在對成像系統通帶內獲取的圖像低頻信息進行復原的基礎上，恢復其截止頻率以上的高頻信息的過程。

圖1 圖像獲取過程示意圖

由于在頻域中很難有效表達圖像中目標的運動信息，近些年大部分研究工作都集中在空域法。其中主要包括反向迭代投影法(IBP，Iterative Back Projection)［2］，凸集投影法(POCS，Projection Onto Convex Sets)［3］，最大后驗概率估計法(MAP，Maximum A Posteriori)［4］和一些濾波方法，相比傳統的插值方法，能夠更好的重建圖像的高頻信息(如邊緣，結構信息等)，獲得更好的視覺效果。在稀疏表示框架下基于字典學習的圖像超分辨率重建算法［5-6］提出了一種更加新穎的思路，從信號、圖像底層的表示模型出發，討論高、低分辨率圖像之間的關系，進而確定高、低分辨率圖像之間的映射關系以及相應的約束，該類方法獲得了高質量的重建結果。然而由于字典學習、稀疏表示等過程具有較高的計算復雜度，很難直接應用在實際中。在保證高質量的圖像超分辨率重建效果前提下，獲得接近或達到工業級(25 幀每秒)的處理速度，一直是圖像/視頻超分辨率重建領域的一大難題，但同時也是一個具有重大研究和實際意義的研究方向。2007年6月NVIDIA 公司推出了統一設備計算架構(CUDA，Compute Unified Device Architecture)。CUDA 是一種將GPU 作為數據并行計算設備的軟硬件體系，被廣泛應用于天文計算、圖像處理、音視頻編解碼等領域，獲得了幾倍、幾十倍，乃至上百倍的加速比。CUDA 為加速圖像/視頻處理提供了一個很好的平臺，使得圖像實時/快速超分辨率重建成為可能。文章重新設計并實現了Non-local IBP［7］算法，實現了基于CUDA 的遙感圖像快速超分辨率重建。

1 Non－local IBP 算法

Non-local IBP［7］算法的主要思想是利用圖像含有非局部冗余信息的特點來改善超分辨率重建圖像的質量，并且通過結合IBP［2］來減小重建圖像的誤差。如圖2所示，大多數自然圖像含有許多重復的結構。這些重復的結構，即非局部冗余信息對于求解圖像處理問題方面的逆問題都有很大的輔助作用。算法流程如圖3所示。

其中:

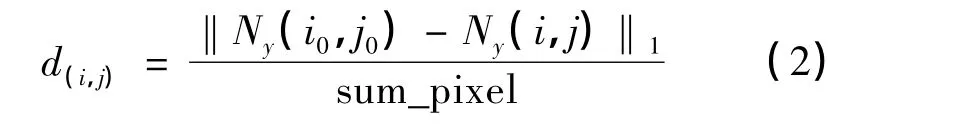
圖2 圖像中重復的結構

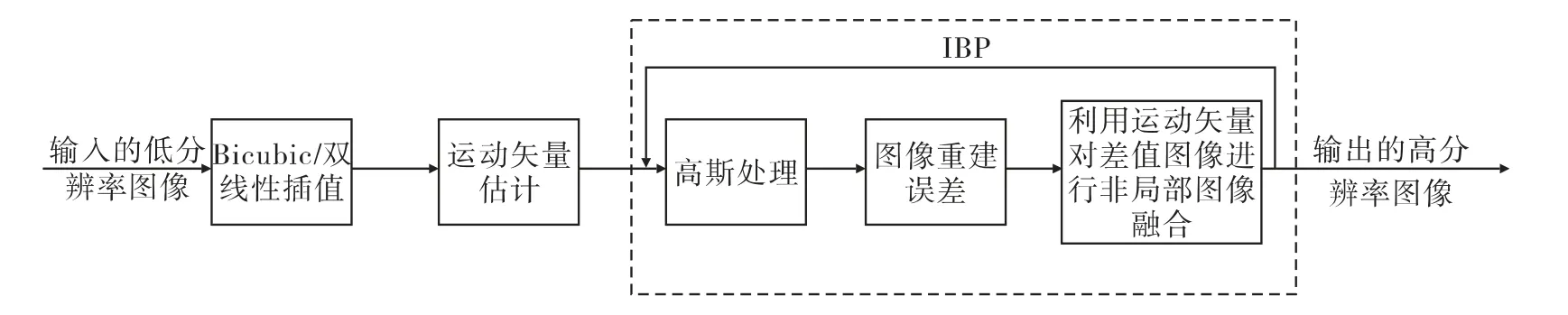
圖3 Non-local IBP 算法流程

其中‖·‖1是L1范數，sum_pixel 是方形鄰域中像素點的個數。如果圖像塊之間的距離d(i，j)比預設的閾值小，說明兩個圖像塊是相似的，并把像素y(i，j)歸于集合S(i0，j0)。S(i0，j0)中包含以及和其相似的像素。在文章的實驗部分中，只選擇保存7 個最小的MAD 值所對應的像素點y(i，j)。同時，記錄下和y(i，j)坐標之差，即vector_x= i0-i，vector_y= j0-j。盡管塊匹配處理可以在整個圖像上進行，但是計算量過大。因此，在實驗中，我們把搜索限定在一個相對較大(21×21)的窗口中。

b.圖像重建誤差:

Il是低分辨率圖像;Ih是高分辨率圖像;D是下采樣矩陣;* 是卷積算子;G是點擴散方程(PSF)［3］，通常是一個高斯核;是圖像重建誤差。

c.利用運動矢量進行圖像融合:第tth次迭代時計算圖像的重建誤差，用重建誤差來更新:

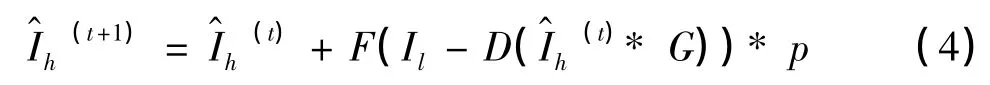
其中F(·)是一個bicubic 插值算子，p是一個向后投影核來控制收斂的速度，對于高分辨率像素的更新，用運動矢量估計得到的7 個低分辨率像素進行更新。

2 Non －local IBP 算法在CUDA 上的實現

CUDA 程序的執行包含兩部分，一部分是在CPU 上串行執行的主機(Host)代碼，另一部分是在GPU 上并行執行的設備(Device)代碼。運行在GPU 上的函數稱為核函數(Kernel)，而運行在CPU上的串行代碼主要完成Kernel 啟動之前的數據準備和設備初始化工作，以及在Kernel 之間進行的一些串行運算。CUDA 程序一般包括以下過程:

在CPU 上初始化數據;

將數據傳輸給GPU;

調用Kernel 進行并行計算;

將結果數據傳回CPU。

Kernel 以線程網格(Grid)的形式組織，每個線程網格包含若干個線程塊(Block)，而每個線程塊包含若干個線程(Thread)，如圖4所示。實質上，Kernel 是以Block 為單位執行的，CUDA 引入Grid 只是用來表示一系列可以被并行執行的Block 的集合。不同Block 之間可以并行執行［8］，但無法進行通信，也沒有執行順序;同一Block 內的線程不僅能夠并行執行，而且能夠通過共享存儲器(shared memory)和_syncthreads()函數相互通信。在Kernel 函數啟動之前需要確定Grid 和Block 的維度。CUDA 提供了dim3 類型(基于uint3 定義的矢量類型，由3 個unsigned int 組成的結構體)的內建變量threadIDx 和blockIDx。這樣，就可以使用一維、二維或三維的索引來標識線程，構成一維、二維或三維的線程塊。

如圖3所示，Non-local IBP 算法主要由bicubic 插值，運動矢量估計，高斯處理，圖像差值和圖像融合這5 個步驟構成，對應到CUDA 架構下相應的核函數依次為bicubic Kernel，運動矢量估計Kernel［9］，高斯模糊Kernel，圖像差值Kernel 和圖像融合Kernel 這5 個Kernel 函數。在核函數被調用前，必須配置核函數的執行參數。例如，對于352×288的低分辨率遙感圖像進行放大因子為2 的超分辨率重建，bicubic Kernel 核函數用來對遙感圖像并行地進行雙三次插值。線程塊Block 的大小blockSize 可取(blockSize.x= 16，blockSize.y= 16)，則線程網格Grid 的大小gridSize 為(gridSize.x= 352/block-Size.x，gridSize.y= 288/blockSize.y)。bicubic Kernel 的配置為bicubic Kernel＜＜＜gridSize，blockSize＞＞＞，一個線程處理圖像的一個像素點。由于GPU實際上是以線程束(Warp)為單位來調度線程執行計算的，因此通常設定M為線程束大小(即32)的倍數，以更加方便、有效地對線程進行管理。CUDA程序執行如圖5所示，首先將圖像數據讀入主機端內存，再將數據從內存傳送到設備端顯存，然后設備端的核函數，即bicubic Kernel，運動矢量估計Kernel，高斯模糊Kernel，圖像差值Kernel 和圖像融合Kernel 依次對顯存數據做并行處理，最后將得到的超分辨率重建的圖像數據從設備端顯存傳送回主機端內存。

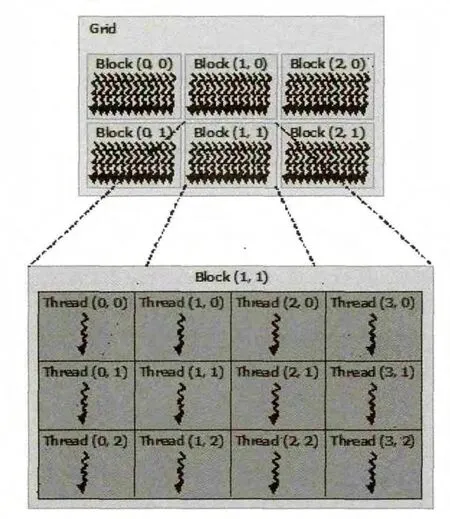
圖4 線程層次結構

3 實驗結果分析

本實驗實現了基于CUDA 的Non-local IBP 算法，對真實遙感圖像進行了尺度大小為2 的超分辨率重建，并與用傳統bicubic 插值算法得到的結果進行了對比。如圖6、圖7 和圖8 三種狀態所示，本文提出的算法重建得到的超分辨率圖像的細節更豐富，對比度更高，邊緣信息更加清晰，圖像的結構特征基本保持完整。

圖5 CUDA 程序執行

表1 是Non-local IBP 算法在CPU 和GPU 兩種環境下的仿真實現的速度對比。如表1所示，相較于CPU 的遙感圖像超分辨率重建速度，GPU 的處理速度有了質的提升，實現了對遙感圖像的快速超分辨率重建。

表2 是Non-local IBP 和bicubic 兩種算法得到的遙感圖像超分辨率重建質量的定量評價。BRISQUE［10］(Blind/Referenceless Image Spatial Quality Evaluator，盲圖像空間質量評估)的值越小(最小值為0，最大值為100)，說明重建圖像的質量越好。由圖6，圖7，圖8，表1，表2 可以看出，基于CUDA 實現的超分辨率重建算法不僅滿足了快速處理的要求，相比bicubic 插值得到的重建圖像，質量要高出很多，增加了圖像的對比度，邊緣保持得很清晰，人工痕跡很少。

圖6 遙感圖像超分辨率重建對比

圖7 遙感圖像超分辨率重建對比

圖8 遙感圖像超分辨率重建對比

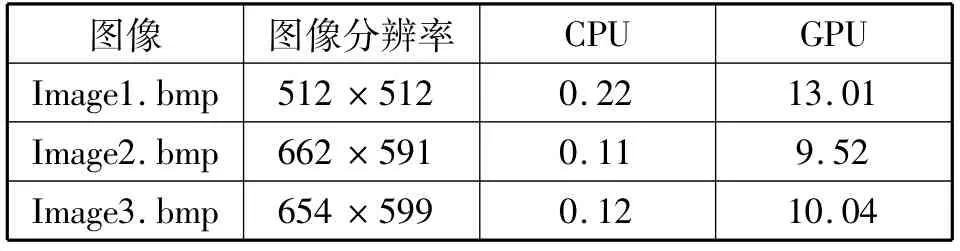
表1 GPU 和CPU 實現Non-local 算法的速度對比(單位:幀/秒)

表2 Non-local IBP 和bicubic 算法超分辨率重建圖像的BRISQUE

4 結束語

文章基于Non-local IBP 算法，在CUDA 架構下實現了遙感圖像的快速超分辨率重建算法，合理利用了Non-local 特性在圖像處理中對描述圖像結構特征的優勢，并能同時包含全局和局部結構特征信息，使得Non-local IBP 超分辨率重建算法得到的圖像細節更豐富，對比度更高，邊緣更加清晰;并且充分地利用GPU 超強的并行計算能力，使得超分辨率重建算法的速率得到了質的提高。

［1］Park S C，Parkm K，Kangm G.Super-resolution image reconstruction:A technical review［J］.IEEE Signal Processing Magazine，2003，20(3):21-36.

［2］S.Dai，M.Han，Y.Wu，and Y.Gong.Bilateral back projection for single image super resolution［C］.In Proc.Int.Conf.on Multimedia and Expo，2007，1039-1042.

［3］H.Stark，P.Oskoui.High resolution image recovery from image-plane arrays，using convex projections［J］.J.Opt.Soc.Am.A，1989，6:1715-1726.

［4］M.Elad，A.Feuer.Restoration of a single superresolution image from several blurred，noisy and undersampled measured images［J］.IEEE Transaction on Image Processing，1997，6(12):1646-1658.

［5］Jianchao Yang，John Wright，Thomas Huang，and Yi Ma.Image super-resolution as sparse representation of raw image patches ［C］.In Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2008，1-8.

［6］Jianchao Yang，John Wright，Thomas Huang，and Yi Ma.Image super-resolution via sparse representation［J］.IEEE Transactions on Image Processing，2010，19(11):2861-2873.

［7］Dong W，Zhang D，Shi G，et al.Nonlocal back-projection for adaptive image enlargement［C］.Image Processing(ICIP)，2009 16thIEEE International Conference on.IEEE，2009，349-352.

［8］張舒，褚艷利，趙開勇，張玉勃.GPU 高性能計算之CUDA ［M］.北京:中國水利出版社，2009.

［9］E.Monteiro，B.Vizzotto，C.Diniz，B.Zatt，and S.Bampi.Applying CUDA architecture to accelerate full search block matching algorithm for high performance motion estimation in video encoding［C］.2011 23rd International Symposium on Computer Architecture and High Performance Computing(SBAC-PAD)，2011，128-135.

［10］A.Mittal，A.K.Moorthy，and A.C.Bovik.No-reference image quality assessment in the spatial domain ［J］.IEEE Trans.Image Process.，2012，21(12):4695-4708.