基于二分法的函數圖像描繪
羅遠峰 LUO Yuan-feng;王凈 WANG Jing
(①遵義師范學院數學與計算科學學院,遵義 563002;②貴州省習水縣樹人中學,習水 564600)
(①School of Mathematics and Computer Science,Zunyi Normal College,Zunyi 563002,China;②Guizhou Xishui County Shuren Middle School,Xishui 564600,China)
0 引言
眾所周知,用近似值的方法描繪出函數圖像,若取值越精確、描點越稠密,所得圖象就越準確。近似求解的方法發展到今天,已經成為數學領域一個獨立的分支。“逐步搜索法、二分法、牛頓法、迭代法、玄截法、拋物線法等”[1],都是計算數學中用于計算近似值的基本方法。二分法已經用于求方程近似的解、求函數零點及極值點的近似值、廣義多項式求值、證明實數連續性中的部分定理、證明不等式等。但卻還未涉足用以描繪函數的圖像。因此,本文闡述了如何用二分法描繪函數圖像及其優越性。
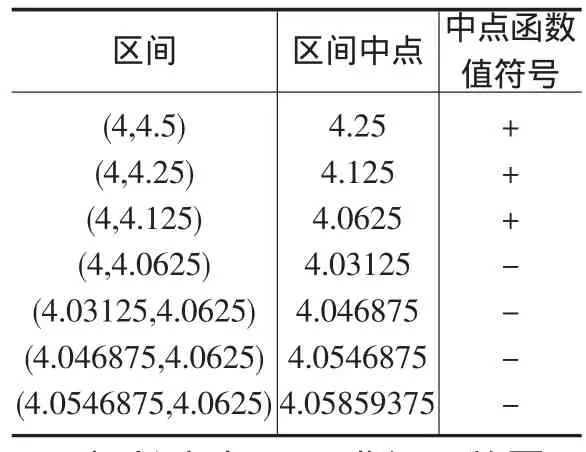
表1 函數零點近似值表
1 二分法求函數零點近似值的步驟
“若函數f(x)在區間[a,b]上連續,且有f(a)f(b)<0,則f(x)在區間[a,b]內有零點。通過不間斷地把函數f(x)的零點所在的區間一分為二,使區間的兩個端點逐步逼近零點,進而得到零點近似值的方法叫做二分法”[2]。求函數零點近似值的步驟:①確定區間[a,b],驗證f(a)f(b)<0,給定精確度 ε;②求中點;③計算 (fc);若 (fc)=0,則c就是函數的零點;若f(a)f(c)<0,則令a(此時零點x0∈(a,c));若f(b)f(c)<0,則令a=c(此時零點x0∈(c,b));④判斷是否達到精確度ε;即若|a-b|<ε,則得到零點近似值a(或b),否則重復②~④。
2 用二分法求函數的零點和極值
用二分法求函數極值的近似值,主要是利用函數的駐點來對函數的極值求近似值,這類問題要求函數本身在給定的區間上具有一階導數,如果所求函數的導函數不是基本初等函數,那么選擇用二分法去求它的近似值完全適用。
例1:求函數y=x4-4x3-x的零點與極值的近似值(精確到 0.01)。
解:因為函數y=x4-4x3-x可看成 x4、4x3和 x三個子函數的代數和,而x4是較 x3、x更高階的無窮小,當 x<0 時,y<0,當 x=0時 y=0,當 x>5 時,y>0。因此,此函數零點所在區間為[0,5)。現利用逐步搜索法尋找函數零點所在區間,取區間長度為0.05求得函數零點所在區間為[4,4.5](表1)。
由于|4.0625-4.054875|<0.01,已達到精確度,所以,可取4.0625作為函數零點的近似值,此時,函數y=x4-4x3-x相應的近似值為y4.0625≈0.1279。因此,函數的一個零點為0,另一個零點的近似值為4.0625。
由于函數在實數集上可導,有y′=4x3-12x2-1,令 y′=0可將上式變為4x2(x-3)-1=0,顯然,當 x=0時,y′<0,當 x=4 時,y′>0。當 x<0 時,y′<0,當 x>4 時,y′>0。因此導函數 y′=4x3-12x2-1的極值點的近似值所在區間為(0,4)(表2)。
由于|3.0234375-3.03125|=0.0078125<0.01,因此,導函數方程的零點近似解可取為x=3.02734375。又因為x=3.02734375 時 y′>0,x=3.0234375 時 y′<0,所以函數 y=x4-4x3-x的極值點的近似值為y≈-31。

表2 函數極值近似值
3 用二分法求函數的拐點
函數拐點是函數圖象上凸和下凸的分界點,而函數的凸性在具體描述函數的性態和證明不等式方面有廣泛的運用。因此,利用二分法求函數拐點的近似值能夠更準確地描繪函數的圖像,拓展二分法的應用。在求函數拐點的近似值時,仍需要從函數拐點的定義入手,利用函數二階導數的性質來為二分法的應用提供條件。所以,要求函數具備二階導數。
例2:求函數y=x4-4x3-ln|x|(x∈R,x≠0)的零點、極值點、拐點的近似值(精確到0.01),并描繪函數的圖像。
解:由于此函數在(x∈R,x≠0)上存在二階導數,其二階導函數為,令 y″<0,利用逐步搜索法取區間長度為0.5,得出二階導函數的零點所在區間為(1.5,2)和(0,1),區間端點導函數值然后求二階導函數零點的近似值。
由于|1.976525-1.98437125|<0.01,|0.375-0.3828125|<0.01,因此可取二階導函數的零點分別為x1=0.375,x2=0.976525。此時,y1≈0.97,y2≈-16.41。由函數拐點的定義可知,(x1,y1)是函數的拐點,又因為(x2,y2)左側下凸,右側下凸。所以(x2,y2)不是函數的拐點。參照例1的方法,求得函數y=x4-4x3-ln|x|的零點近似值分別為x3=0.5495,x4=4.015;導函數的零點近似值分別為x5=-0.4175,x6=3.0215,此時,函數極值的近似值分別為 y5≈1.2,y6≈-29.37。
4 用二分法描繪函數圖像的認識
4.1 用二分法描繪函數圖像的優越性 利用二分法描繪函數圖像主要是利用函數的零點、極值點、拐點的近似值,以整體把握函數的基本性質,進而描繪出函數的圖像,而且在求某些函數的漸近線上仍然可以運用二分法。另外,“基于區間套定理的理論基礎結合‘代整為零,積零為整’的數學思想,二分法可以有效證明不等式。”[3]“二分法簡單直觀,特別適合用來求迭代法的初值。”[4]總之,用二分法求近似值的思想易于理解,便于掌握。
4.2 用二分法描繪函數圖像的弱點及改進設想 從以上幾個例子容易看出,“用二分法求函數零點近似值收斂速度太慢”,如果不借助計算機,很難操作,且用二分法求函數的零點、極值點、拐點方面常常很難找全零點所在的區間。另外“用二分法求函數零點時,如果在區間[a,b]內有多個實根,則單獨利用二分法只能得到其中一個實根”[5]。因此在找函數的零點問題上,可考慮用函數的極值、單調性、拐點等來探求函數零點的近似值,可以綜合運用其它來描繪函數圖像,這樣便解決了收斂速度過慢的問題,但在這方面需要進一步探索。
5 結束語
本文僅僅研究了二分法描繪函數圖像的一些步驟,結合自身實踐對該方法的優劣與發展提出了看法和設想,認識難免膚淺,還需今后進一步探究。另外,也期待對該方法有研究者的交流指導。
[1]肖筱南.現代數值計算方法[M].北京:北京大學出版社,2003,7(第1版):80-83.
[2]人民教育出版社,課程教材研究所,中學數學課程教材研究開發中心.普通高中課程標準實驗教科書數學必修1(A版)[M].北京:人民教育出版,2007,1(第 2版):89-91.
[3]劉小明.二分法思想的應用[J].高中生之友,2011,12(9):27-28.
[4]鄭成德,李志斌,王國燦,孫日明,李炎淼.數值計算方法[M].北京:清華大學出版社,2010,9(第1版):142-158.
[5]徐士良.數值分析與計算法[M].北京:機械工業出版社,2007,1(第1版):154-156.

