衛星高度計數據樣本大小對潮汐信息提取的影響＊

宋箐陽，于華明，陳學恩，李曉榮

（中國海洋大學1.海洋環境學院；2.環境科學與工程學院，山東 青島266100）

海洋衛星測高技術逐步興起，極大的推動了全球海洋潮汐學研究的發展，特別是1992年發射的TP衛星及其后續衛星，它所提供的海面高度誤差在5cm以內，數據質量明顯優于之前的衛星高度計數據。20年來其數據應用于物理海洋學研究，取得了豐碩的成果，同時也大大的促進了海洋潮汐動力學的發展。

Cartwright D.E.和R.D.Ray[1]最先從衛星高度計數據中提取潮汐信息，他們選用重復周期為17.050 5d的衛星高度計GEOSET第1年的數據，采用正交響應法，在每個星下點獨立的進行潮汐分析，詳細討論了混淆效應對潮汐組分分離的影響，將得到的主要半日分潮M2和S2的調和常數與沿岸驗潮站進行了比較。Ma X.C等[4]將Cartwright等使用的方法應用于更為精確的T/P數據處理上，同樣使用1年的觀測數據，只是在內插的過程中考慮了地形的影響，從而分離了8個主要分潮和3個長周期分潮，得到了比Cartwright等更精確的計算結果。Gary D.Egbert等[3]引入了T/P衛星數據的同化反演算法以建立全球潮汐模型，而C.Le Provost等[4]將這種算法應用到有限元水動力潮汐模型中，也取得了不錯的結果。但是即便是以上述2種方法為基礎的最新潮汐模型TPXO7.2和FES2004，也從沒有引入過18.6年的衛星高度計數據。其中TPXO7.2僅僅包含T/P 和 Jason－1的數據，而FES2004在同化的過程中只是引入了T/P衛星在一部分軌道交叉點的數據。然而自1992年8月TP衛星發射以來，至今將近20年，數據觀測的時間長度超過了18.61年，之前的衛星高度計數據分析所使用的數據樣本較小，大都未考慮T/P后續衛星Jason－1和Jason－2的加入，樣本更大的高度計數據的引入是否可以進一步提高潮汐分析的精確度，未來衛星高度計數據的增加對于海洋潮汐研究是否還具有重要意義？本文運用最新的衛星高度計數據，結合 T/P，Jason－1和Jason－2共18.6年的觀測數據，分析探討衛星高度計數據觀測時間長度的增加即觀測樣本的增大對潮汐分析結果的影響，以及沿軌衛星高度計數據使用過程中存在的一些問題，旨在為上述問題的解答提供一定的參考。

1 數據和方法

1.1 數據

1.1.1 衛星數據 TOPEX/POSEIDON以及它的后續衛星Jason－1和Jason－2是由美國航空航天局（NASA）和法國國家空間研究中心（CNES）合作開展的高度計衛星項目。其中TOPEX/POSEIDON衛星于1992年8月發射升空，它的重復周期為9.915 6d，1個重復周期由127個升軌和127個降軌所組成。最南端至最北端（或最北端至最南端）之間的星下點軌跡被稱為1個pass。由此可見，在1個衛星重復周期中，共有254個pass，并分別由1～254來編號表示。同樣，Jason－1和Jason－2衛星也沿著與T/P衛星相同的軌道運行。

本文所使用的衛星數據是由法國空間研究中心（CNES）和美國加州工學院噴氣實驗室（JPL）提供的綜合地球物理數據記錄（MGDR）和地球物理數據記錄（GDR），數據自1992年8月～2011年8月，共18.6年。作者將這些數據按衛星傳感器分為3段，分別是TP（T/P衛星數據，Cycle2～Cycle365），J1（Jason－1衛星數據，Cycle1－Cycle259），J2（Jason－2衛星數據 Cycle1－Cycle120）。

MGDR和GDR數據提供的測量值是衛星距海平面高度（hsat）以及衛星距參考橢球面的高度。海表面高度（SSH）可以由如下（1）式計算：

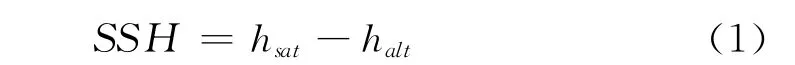
然而衛星測距（衛星相距海表面的高度測量）會受到大氣等物理因素的影響，所以需要進行數據訂正，分別包括濕對流校正，干對流校正，電離層校正和電磁偏差校正，這些物理訂正以Δh表示。這些訂正所使用的數值由數據本身所提供。雖然本文并沒有考慮徑向軌道誤差，但是從升軌和降軌交叉點上數據計算結果的比較中，本文仍然可以估計出該誤差造成的影響。在潮汐計算中，研究者更關心多種周期組分疊加的海面高度變化，而不關心它的絕對值，所以本文將平均海平面高度從數據中減去，即將參考系平移到平均海平面高度處，同時去除固體潮（SET），極潮（PT）和負荷潮（LT）的影響，由（2）式計算所得到的數據用于本文的潮汐分析。

1.1.2 站位數據 潮汐測站數據取自NOAA和夏威夷大學海平面中心提供的 GLOSS（The Global Sea Level Observing System）逐時數據，其在66°N～66°S共有256個測站，站位分布圖如圖1所示。

圖1 衛星交叉點及驗潮站位置Fig.1 Location of crossover points（crosses）and tide gauge stations（dots）

1.1.3 同化反演模式TPXO7.2 本文選用全球潮汐反演同化模式TPXO7.2的數據來進行對照分析。TPXO7.2覆蓋了包括北冰洋在內的全球海域，分辨率為1/4（°）。該模式在同化過程中除了引入T/P系列高度計數據外，還包括有GRACE，ERS的衛星數據以及一些測站數據，這些數據能幫助提高其在極地以及淺水中的準確度。作為成熟的全球潮汐模式，TPXO7.2輸出的M2分潮振幅均方根誤差在大洋中只有1～2cm，與一些淺水站位比較也只有6cm左右，其可靠性毋庸置疑。有關該模式的具體方法請參考Gary D.Egbert等和 Gary D.Egbert等[5]。

1.2 方法

1.2.1 網格點選取 按照上一節所述的方法處理完數據并去除缺省值之后，本文又以偏離平均海平面不超過5m的標準（因為在全球大部分海區，半潮差都在5m以內）進行質量控制，剔除由隨機因素造成的奇異值。通過衛星高度計數據提取潮汐信息的關鍵步驟在于建立合適的時間序列。衛星雖然沿著固定的軌道運行，但對于不同的cycle，其相對應的觀測點位置卻存在偏差。一般的處理方法是選擇1個確定的參考軌道，并在該軌道上確定要作為計算點的觀測點位置，再進行插值。本文同樣采用了這種方法，將缺測點最少的cycle作為參考軌道。介于對全球海洋分辨率以及計算量的考慮，在參考軌道上，每隔10個觀測點取1個點（相距約60km，時間間隔為10s）來作為固定的計算點。然后將同1個pass不同cycle上的測點按照（3）式的插值形式（距離加權內插方法）插值到計算點上，以形成時間間隔為9.915 642d的時間序列。其中（3）式是 Tetsuo Yanagi et al[6]提出的1種用于將潮汐調和常數預報所得的水位插值到整個區域的插值方法。

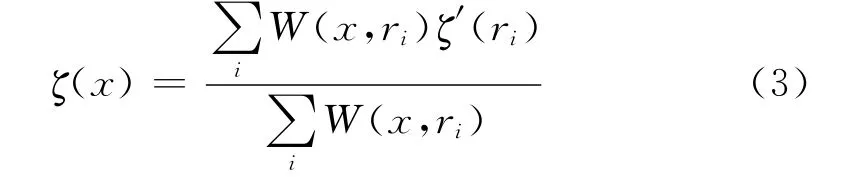
式中：x為網格點的位置；ri為被插值點的位置；W為距離插值的權函數；L為距離插值的相關半徑。本文取L＝12km，覆蓋4個測點（衛星在1個軌道上測量的每2個星下點，相距約為6km）左右。

1.2.2 調和分析與混淆問題 本文用上述方法在衛星覆蓋的全球海域內共確定了49 248個計算點，并通過將不同cycle的觀測數據插值到這些點上，在每1個點上都構成了水位的時間序列。但是由于這個時間序列的Nyquist頻率遠低于主要的潮汐頻率，在調和分析的過程中，高頻混淆會對結果造成一定影響。根據Rayleigh準則，12個主要的分潮只有在數據長度滿足表1的要求時才能被完全分離開。當單獨使用TP和J1來進行調和分析時，沒有將長周期半年潮Ssa和半日潮K2考慮在內，因為這些分潮不能分離，會影響K1和P1分潮的分析結果。而對于結合多個衛星的18.6年高度計數據，Ssa和K2分潮也都可以分離。

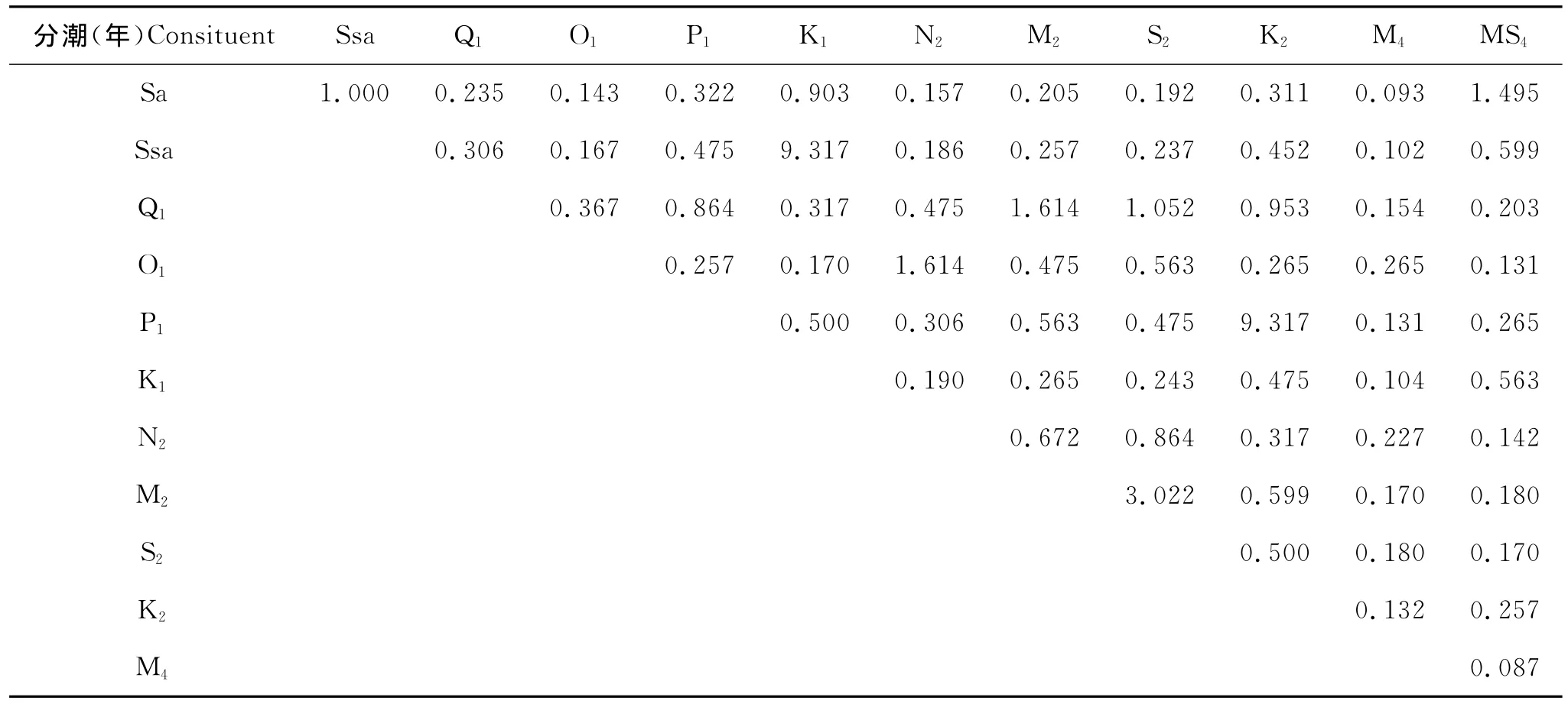
表1 12個主要分潮基本分辨所需資料長度Table 1 Alias synodic periods of each pair of 12main constituents /a

1.2.3 衛星數據時間錯位問題 除了上述的混淆問題，在將來自不同衛星高度計的數據結合到一起進行分析的過程中還存在著時間序列錯位的問題，這個問題是由于新老衛星的更替造成的。2001年Jason－1發射升空，與T/P衛星在相同的軌道上運行，而2002年8月15日。T/P衛星通過變軌移動到了與原衛星軌道交錯的軌道上，即變軌后T/P衛星的pass（星下點軌跡）在Jason－1衛星的2個pass之間。這樣能夠在T/P衛星停止工作以前臨時地增加衛星高度計的觀測分辨率（AVISO 2002）[7]。而在2008年6月，Jason－2發射后，Jason－1也同樣進行了變軌。可以看到，在新衛星發射之后，舊衛星變軌之前，存在一段時間2個衛星同時在1個軌道下運行。這就意味著2個衛星在對同1個點進行觀測時必定會有一段時間差，按照AVISO提供的使用手冊，這個偏差是70s。盡管在70s的時間內潮汐變化很小，但是忽略這70s的時間差進行調和分析是否會影響到分析結果的準確性仍然存在疑問。本文雖然在進行調和分析的過程中忽略了這個時間差，但是結合來自不同衛星的數據進行分析與單獨使用T/P衛星數據分析所得結果的過程中，本文詳細討論了這個時間偏差所帶來的影響。

2 結果分析

2.1 與潮汐測站結果的比較

為了明確各組數據所得的調和常數是否準確，本文將其插值到256個大洋及島嶼站點上，并與潮汐測站的結果進行比較（見表2）。從表中看，對于不同的分潮來說，衛星數據分析所得的分潮遲角與實測相比，相差最小的是M2分潮，遲角差的平均值為6.64°，最大的是K1分潮，平均值為10.02°；振幅相差最小的是O1分潮，振幅差的平均值為1.77cm，最大的是 M2分潮，達到3.84cm。但是全球海洋中M2分潮平均振幅要比全日分潮K1和O1以及半日分潮S2要大。事實上，M2分潮振幅的平均相對誤差（ΔH/H）為0.083 2，而S2，，K1，O1的振幅平均相對誤差分別為0.105，0.115和0.173。可見，利用衛星數據調和分析出的 M2分潮振幅在這4個分潮中是最為準確的。

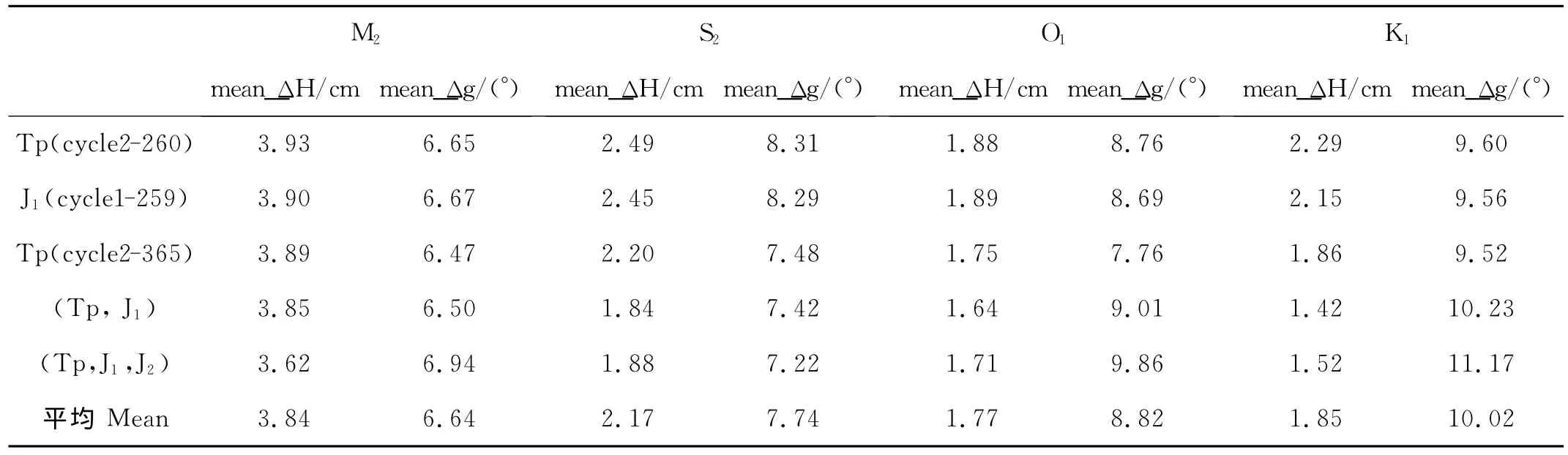
表2 多組測高數據計算的調和常數與驗潮站比較結果Table 2 Comparison between satellite－derived harmonic constants（5groups）and ground－derived harmonic constants（Mean＿ΔH and mean＿Δg are the mean absolute errors）

而從各組數據分析得到的振幅與實測數據的比較來看，參與分析的數據樣本越大，其所得的M2分潮振幅與實測的相差越小，但是同樣的情況并沒有發生在另外3個分潮上。盡管結合T/P和Jason－1 2顆衛星的數據進行調和分析時，即表中（Tp，J1）所示，其得到的調和常數與實測相比，4個分潮的振幅差比僅使用T/P衛星數據分析有較大的減小（0.5～1cm）。但是當把Jason－2的數據也加入計算時，分析所得的除M2分潮之外的其他3個分潮與實測相比的振幅差反而增大了。雖然這種振幅差的增大都只在0.1cm左右，但是其產生的原因卻不能被忽視。另外，隨著參與分析的數據樣本的增大，計算得到的調和常數與實測的結果相比，全日潮的遲角差明顯有而增大的趨勢，而半日分潮的情況卻有點復雜，M2分潮的遲角差增加很小，S2分潮的遲角差甚至隨著數據長度的增加而減小了。而造成遲角計算誤差的主要有如下2種因素：（1）調和分析過程中忽略了2顆衛星在同一軌道運行時（tandem mission）的70s的時間差；（2）衛星測量時的隨機時間誤差。然而無論是哪一種單獨的原因都不會造成像S2分潮所表現出的遲角差減小的情況，而測量誤差的隨機性也很難造成像2個全日分潮這樣遲角差趨勢性增大的現象。但是作者無法判斷忽略70s的時間差進行調和分析會造成什么樣的影響，特別是期間還存在有高頻混淆。于是本文做了如下的理想性試驗，首先假設1個理想的潮汐水位，他只有單個分潮作用，并且按照3個衛星一樣的取樣間隔與取樣長度進行取樣。同樣在忽略2顆衛星之間70s的時間差進行調和分析后發現，在水位僅由單個分潮作用的前提下，這70s的時間差對不同頻率的分潮都沒有造成振幅計算上的誤差，但是對遲角計算卻產生了影響，其造成的具體遲角誤差如圖2所示。

圖2 理想化實驗遲角誤差圖Fig.2 Error of phase－lag in idealized experiment

從圖中看，對于半日潮，將2顆衛星的數據放在一起調和分析的結果將造成0.2°左右的偏差，而對于全日潮，這種偏差只有0.1°左右，并且對于所有頻率的分潮，將第3顆衛星的數據加入計算會使得遲角差進一步增大。其中，半日潮增大到0.3°，而全日潮增大到0.15°。可見，單單是這種因素并不能造成表3所呈現的現象。于是為了看到混淆的影響，又不失理想化，本文將表3中的4個分潮疊加在一起。通過對這4個分潮產生的理想水位進行忽略70s偏差的調和分析來檢驗混淆的影響，這樣得到的4個分潮的振幅計算誤差僅為0.001cm左右。當然 ，如果是在實際的情況中，因為分潮數目較多，混淆的影響肯定要大的多。再加上衛星測量的誤差，才造成了這幾厘米的振幅誤差量級。而遲角計算誤差的結果反應在圖2中如＋所示，由于混淆的存在，O1分潮的遲角差減小了，2個半日分潮則都增大了。可見混淆確實會對遲角的計算誤差產生影響，雖然與表3的結果相比，這種影響要小的多。但是由于在實際的調和分析中考慮的分潮并不僅限于這4個，具體能產生什么樣的結果仍然需要進一步的討論。盡管如此，這個實驗仍然能夠表明，表2這種現象有非常大的可能是在忽略70s的時間差進行調和分析的過程中由于混淆而產生的。

2.2 M2同潮圖的對比

為了更進一步的檢驗本文所得到的潮汐經驗模式的結果，本文將Tp，J1，J2三者共18.6年的數據計算所得的 M2分潮調和常數插值到66°N～66°S，1（°）×（1°）的規則網格上，并繪制了同潮圖（見圖3a），而與其進行對比的圖3b則是根據OTIS輸出的全球潮汐模式TPXO7.2的M2分潮調和常數進行繪制的。為了在一定程度上避免由于模式計算點的不同而造成的插值誤差，本文中OTIS輸出的TPXO7.2的數據與經驗模式計算點的位置一致。通過比較可以看出，兩者結果基本相似，遲角振幅相差很小，大洋潮汐與近岸潮汐相比較小，與平衡潮的潮差比較接近。兩者在太平洋中各有7個M2分潮無潮點，位置基本一致，特別是對于大洋中部的潮汐波系統。菲律賓海的2個相距較近的潮汐系統的結構也都體現了出來，但是兩者位于所羅門海的無潮點位置有所偏差，同樣的情況也發生在印度洋及大西洋中。在這2個大洋中，本文所得到的經驗模式和OTIS輸出的TPXO7.2的旋轉潮汐系統的數目和分布是一致的。大洋中部無潮點的位置也相差較小，稍有區別的是在臨近陸架或島嶼的無潮點上，如在澳洲大陸西南角處以及位于加勒比海的東側的無潮點。除此以外，TPXO7.2的插值結果更為平滑，這是因為OTIS所提供的雙線性插值是經過了8點平滑的，而在使用本文所得到的調和分析結果進行插值時沒有做任何處理。

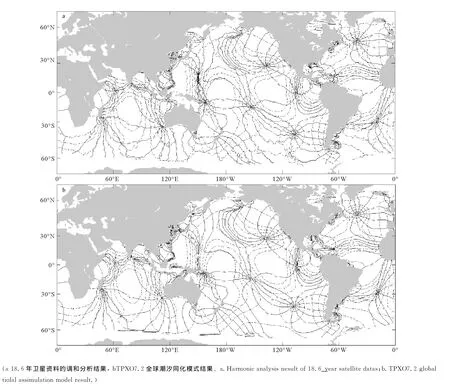
圖3 M2分潮同潮圖Fig.3 Cotidal charts of M2constituent

從上述比較中可以看到，雖然與其他潮汐模式所得到的同潮圖相比在高緯度及近岸地區有很大的缺陷，但這是由衛星的覆蓋范圍以及計算點的選取所決定的。由本文的方法所建立的全球經驗潮汐模式還是可信的。從圖中看，北半球的M2分潮潮波系統幾乎都成逆時針旋轉，而在南半球卻并非如此。赤道太平洋地區存在2個M2分潮的高值區，其振幅都超過了40cm，同樣的情況也發生在印度洋中部。另外，總體來看在北半球東邊界的M2分潮振幅要大于西邊界，南半球的情況則相反。

為了與TPXO7.2進行更進一步的比較，本文將調和分析T/P衛星10年數據以及3顆衛星18.6年數據所得到的M2分潮振幅，分別減去OTIS輸出的TPXO7.2模式的結果，并插值到1（°）×1（°）的網格上（見圖4）。從圖中可以看到，總體上，TPXO7.2與另外2個模式的M2振幅差都在1cm左右。一些沿岸地區，特別是太平洋和大西洋的西海岸，則相差較大。研究者認為這是由于TPXO7.2在同化過程中引入了較多沿岸測站和其他一些衛星的數據所致。另一方面，圖4a和4b的對比說明，18.6年數據的計算結果明顯更接近TPXO7.2，其在大洋中誤差為0的部分要遠大于僅由T/P衛星數據計算所得到的結果，這體現了長時間大樣本數據分析的優越性。

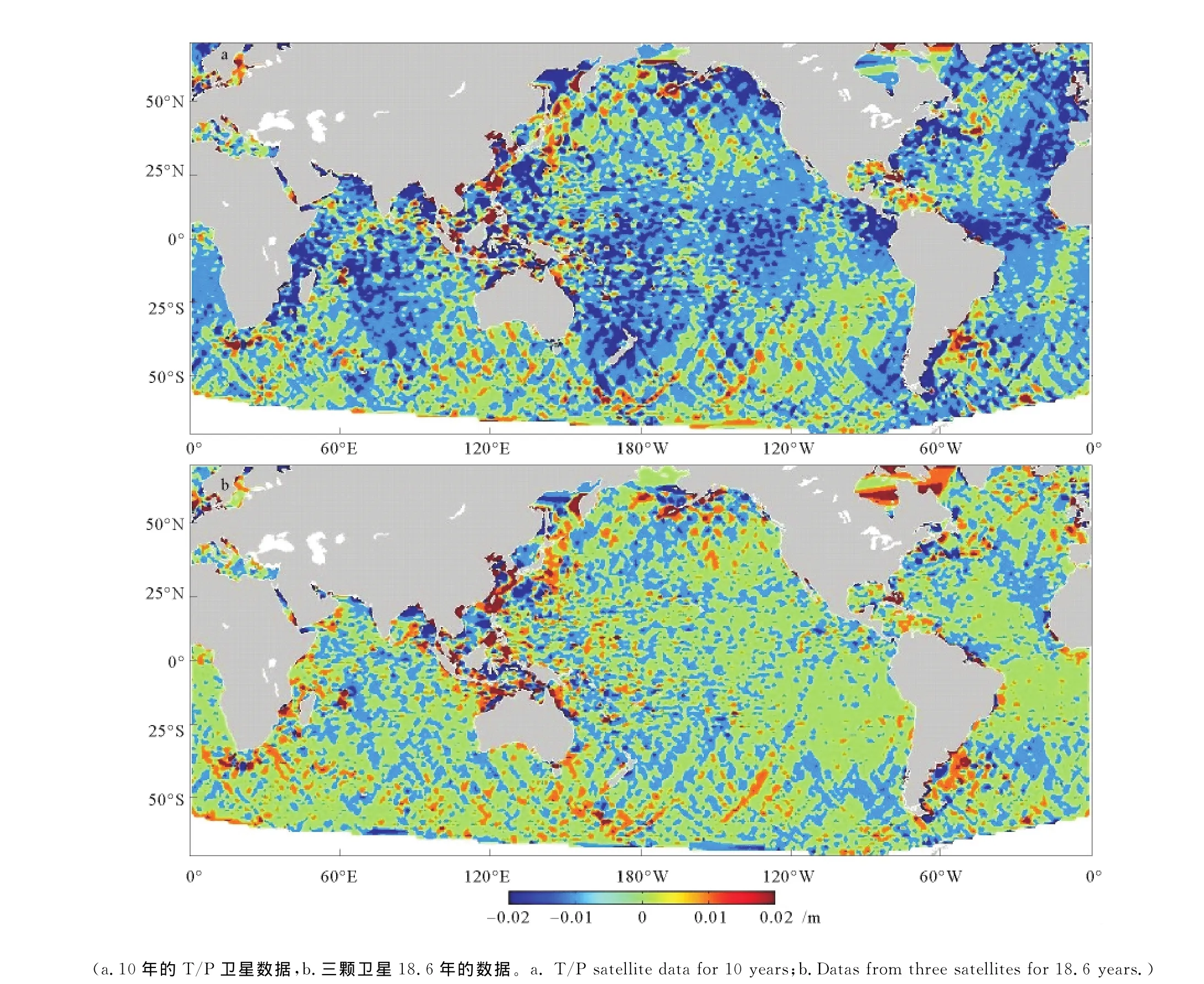
圖4 經驗模式與TPXO7.2的M2分潮振幅偏差Fig.4 The different of amplitude for M2constituent between empirical model and TPXO7.2

2.3 潮汐信息提取精度分析

高度計衛星的交叉點（Crossover Point）指的是衛星星下點軌跡中升軌與降軌的交點。由于在這些點上同時具有2個pass上的觀測數據，所以能夠通過不同pass在這些點上調和分析結果的比較來討論調和分析的精度。

本文選取60°S～60°N之間的交叉點（共5 328個，見圖1）進行統計分析。本文對升降軌各自在交叉點上的7年以及10年T/P衛星數據，7年Jason－1數據，結合T/P與Jason－1兩者的數據以及結合3顆衛星的數據分別進行調和分析，并比較由2個軌道的數據計算所得到的4個主要分潮（M2，S2，O1，K1）以及周年潮Sa，結果如表3～5所示。其中由（4）式定義的Δ來指示升降軌數據計算得到的調和常數的差，而H則為由升降軌數據在交叉點處計算得到的分潮平均振幅，Δ/H則可以用來指示調和常數的相對偏差。

表3 多組測高數據交叉點處全日潮調和常數比較（‘（）’代表組成整體使用）Table 3 Difference between harmonics derived from ascending and descending passes at crossover

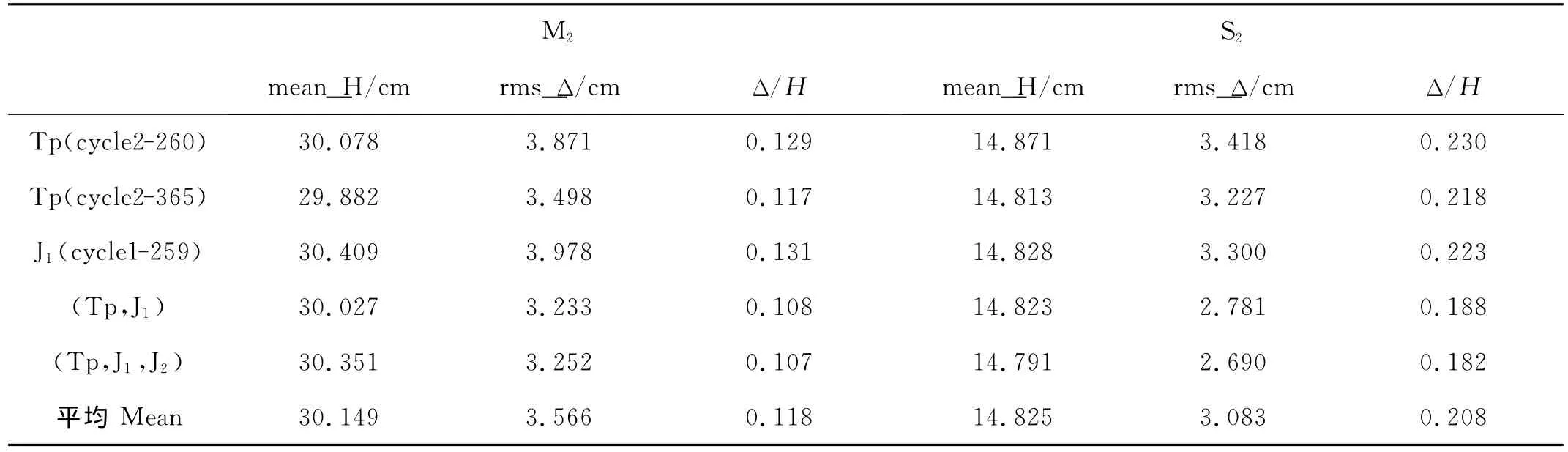
表4 多組測高數據交叉點處半日潮調和常數比較Table 4 Difference between harmonics derived from ascending and descending passes at crossover points：Semidiurnal Constituents

下標a和d分別代表升軌和降軌，g為分潮遲角。該式是由（Fang et.al 2004）[8]提出的。需要說明的是，由于衛星高度計在這些區域的測量精度本來就存在疑問，特別是當衛星從陸地進入海洋時[9]，表中H的平均值以及Δ的均方根值去掉了位于近岸海域的21個交叉點，這些點上的Δ異常大。

從表中看，不同樣本數計算得到的M2分潮Δ的平均值是除長周期分潮Sa外最大的，為3.566cm。而O1分潮的則最小，為2.484cm。但是由于 M2分潮的振幅較大，其Δ/H的平均值只有0.118，要小于表中所有的半日潮和全日潮。K1分潮則由于振幅較小而成為了Δ/H最大的分潮，其值達到0.226。另外，對于計算得到的某1個分潮的調和常數，隨著參與調和分析的高度計數據樣本數的增加，其Δ/H值是趨于減小的，在樣本數增大到使數據能覆蓋18.6年的時間長度時，其計算出的4個主要分潮 M2，S2，O1，K1的Δ/H值分別只有0.107，0.182，0.166，0.151，都遠小于單獨使用1個衛星的數據TP或者J1所得到的結果。顯然，要說明這個調和分析的精度隨著樣本數的增加而提高的現象，比較來自同1個衛星的不同樣本數數據的計算結果更有說服力。比如，來自T/P衛星的2組不同樣本大小的數據，Tp（cycle2－260）和 Tp（cycle2－365），用他們分別計算得到的M2分潮調和常數的Δ/H值為0.129和0.117，樣本數較大者Δ/H較小。而由這2組數據調和分析得到的其他分潮的調和常數也有類似的結果，他們都驗證了上述的現象。除此之外，對于來自不同衛星的相同樣本數的數據，如J1（cycle1－259）和Tp（cycle2－260），還存在著另外一個現象。在他們的結果中，由J1計算所得到3個主要分潮S2，O1，K1的調和常數，其Δ/H值都要小于由Tp（cycle2－260）計算的結果，而兩者M2分潮的結果其實很接近，Δ/H的差僅為0.002。因為Δ/H不僅受制于調和分析的計算精度也受制于衛星的觀測精度，所以這在一定程度上說明了Jason－1衛星的數據精度要好于T/P衛星。除了這4個主要分潮，長周期分潮Sa比較特殊。從表中看，在使用7年的數據時，計算得到的Sa的振幅遠遠大于使用10，17及18.6年的數據進行調和分析的結果，而且隨著樣本數的的增大，不僅Δ/H在減小，調和分析得到的分潮平均振幅H也在減小，這反映了調和分析的過程中高頻混淆的影響，正是由于高頻信息無法完全分辨，計算時便會混淆在長周期的周年潮Sa中，使得出的Sa分潮的振幅偏大。

表5 多組測高數據交叉點處周年潮調和常數比較Table 5 Difference between harmonics derived from ascending and descending passes at crossover points：annual constituents.

3 結論

（1）通過與沿岸站位的比較表明，高度計數據樣本數的增加在一定程度上有利于提高反演分潮振幅時的準確度。將不同樣本數的數據計算出的M2分潮振幅與TPXO7.2輸出的結果進行比較也印證了這一點。但是，不同衛星之間的數據存在70s時間差，在結合不同衛星的數據并忽略這個時間差進行調和分析時，由于混淆的作用，使得分析反演遲角過程中產生的誤差會有所改變。對于全日潮K1，O1以及半日潮M2，誤差會增大，而對于半日潮S2，誤差會減小。

（2）在交叉點上，對于不同樣本大小的數據，通過比較在升降軌2個軌道上各自計算出的調和常數，表明本文所使用的調和分析方法的計算精度隨著參與分析的衛星數據樣本數的增加而提高。相比于單獨使用10年T/P衛星數據分析得到的調和常數，利用18.6年的衛星數據計算得到的K1，O1這2個全日分潮的Δ/H減小了7%左右，而半日分潮M2和S2則分別減小了1%和3.6%。

（3）本文分析所獲得的經驗模式與基于全球潮汐模式TPXO7.2的結果所繪制的 M2分潮同潮圖的對比表明，兩者反映的大洋潮汐特征基本一致，只有3個陸架近岸的無潮點位置有微小的出入。而高緯及近岸潮汐信息的缺失則是由衛星覆蓋區域以及本文所選擇的計算點分辨率（同一軌道上相距60km左右）的原因造成的，加密計算點將在一定程度上解決這個問題。可見本文所建立的這個基于多個高度計衛星18.6年數據的全球經驗模式是可信的。

[1]Cartwright D E，Ray R D.Oceanic tides from Geosat altimetry[J].J Geophys Res，1990，95：3069－3090.

[2]Ma X C，Shum C K，Eanes R J，et al.Determination of ocean tides from the first year of TOPEX/POSEIDON altimeter measurements[J].Geophys J Res，1994，99（C12）：24809－24820.

[3]Gary D Egbert，Andrew F Bennett.TOPEX/POSEIDON tides estimated using aglobal inverse model[J].J Geophys Res，1994，99（C12）：24821－24852

[4]Le Provost C，Lyard F，Molines J M，et al.A hydrodynamic ocean tide model improved by assimilating a satellite altimeter－derived data set[J].J Geophys Res，1998，103（C3）：5513－5529.

[5]Gary D Egbert，Svetlana Y Erofeeva，Richard D Ray.Assimilation of altimetry data for nonlinear shallow－water tides：Quarter－diurnal tides of the Northwest European Shelf[J].Continental Shelf Research，2010，30：668－679.

[6]Yanagi T，Morimoto A，Ichikawa K.Co－tidal and co－range charts for the East China Sea and the Yellow Sea derived from satellite altimetric data[J].J Oceanogr，1997，53：303－309.

[7]AVISO.AVISO and PODAAC User Handbook IGDR and GDR Jason－1Products，SMM－MU－M5－OP－13184－CN[M].USA：AVISO，2008.

[8]Fang Guohong，Wang Yonggang，Wei Zexun，et al.Empirical cotidal charts of the Bohai，Yellow，and East China Seas from 10 years of TOPEX/Poseidon altimetry[J].J Geophys Res，2004，109（C11006）：doi：10.1029/2004JC002484.

[9]董曉軍，馬繼瑞，范振華，等.利用衛星高度計資料提取黃海、東海潮汐信息的研究[J].海洋與湖沼，2002，33（4）：672－678.