基于VSC技術的交直流混聯系統靜態電壓穩定分析

毛志強

（濟南供電公司，山東濟南250001）

基于VSC技術的交直流混聯系統靜態電壓穩定分析

毛志強

（濟南供電公司，山東濟南250001）

大區域電網間采用異步互聯是未來電網發展趨勢，直流輸電技術是實現異步互聯的關鍵技術。VSC-HVDC輸電技術是直流輸電技術的主要發展方向之一，與傳統的較為成熟的PCC及CSC技術不同，基于VSC技術的交直流混聯系統靜態電壓穩定性問題研究較少，對此問題進行較為深入的探討，提出基于VSC技術的交直流混聯系統靜態電壓穩定性分析方法，并使用算例進行AC/VSC-HVDC系統的電壓穩定性計算，算例結果證實算法的可行性。

靜態電壓穩定性；VSC-HVDC輸電技術；交直流混聯系統

0 引言

大區域電網直流互聯是保證大電網安全穩定運行的有效手段，直流互聯可以使所聯接的兩交流電網非同步運行，實現了兩互聯交流電網的隔離，利于兩非同步交流電網的進一步發展。電壓源換流器高壓直流輸電（VSC-HVDC）技術采用大功率全控型IGBT器件，與傳統的PCC-HVDC和CSC-HVDC相比優勢明顯［1］。

自1990年，加拿大學者提出VSC-HVDC輸電技術至今，關于該項技術的研究多集中于VSC擴容及系統控制器設計，對基于VSC技術的交直流（AC/ VSC-HVDC）混聯系統穩定性研究較少。在已公開的文獻中，文獻［2-4］利用d-q變換方法，對VSCHVDC系統進行了強制線性化處理，建立起VSCHVDC的穩態數學模型并提出相應的控制策略，但對大容量VSC技術情況下未做分析。而文獻［5］針對短路容量比較低的交流系統，建立VSC-HVDC非線性數學分析模型，并分析了VSC控制器模型對該系統建模的影響，此方法只針對低短路比的交流系統適用，具有一定的局限性。文獻［6］所述VSCHVDC系統的狀態空間數學模型是將直流系統兩側換流器所接的交流系統簡化為理想電壓源進行分析，并未考慮交流系統潮流變化對直流系統的影響，不符合實際系統運行情況。文獻［7］利用VSC兩個控制變量進行推演進而得到換流器的4個被控變量，以此建立VSC-HVDC的穩態數學模型，并提出了VSC的兩個控制量與4個被控變量之間的近似解耦關系。

對于AC/VSC-HVDC混聯系統靜態電壓穩定性分析方面，文獻［8］依據混合勢函數的概念，利用平衡點判定法，分析了交直流混聯系統的靜態穩定性。文獻［9］則是利用李亞普諾夫理論對VSC-HVDC系統的穩定性進行了分析，對交流混聯系統分析仍然較為簡單。總體來講，有關AC/VSC-HVDC混聯系統靜態電壓穩定性的方法還較少，多數研究仍然集中于控制策略分析。

本文在建立AC/VSC-HVDC混聯系統的穩態數學模型的基礎上，探討將延拓法和交替求解法相結合的AC/VSC-HVDC混聯系統靜態電壓穩定性分析方法，并將此方法應用于基于電壓源換流器的交流／多端直流混聯系統（AC/VSC-MTDC）中，使用算例加以驗證，結果驗證了該方法的正確性和可行性。

1 AC/VSC-HVDC混聯系統數學建模

AC/VSC-HVDC混聯系統的穩態模型是系統靜態電壓穩定分析的基礎。通過VSC的穩態模型及VSC-HVDC的控制方程，得到AC/VSC-HVDC混聯系統的穩態數學模型。

1.1 AC/VSC-HVDC系統交流子系統穩態數學模型

在AC/VSC-HVDC混聯系統中，把交流系統中與VSC換流器直接相連的節點稱為直流節點，其他節點稱為交流節點。假設混聯系統共有n節點、m個VSC換流器，則混聯系統的交流節點數na=n-m，直流節點數為m。

對于交流節點，其節點功率偏差方程和純交流系統一致，為

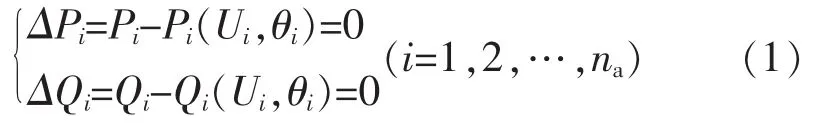
對于節點i，Pi表示其有功功率；Qi表示其無功功率；Ui表示節點電壓；θi表示相角。

對于直流節點，其節點功率偏差方程為

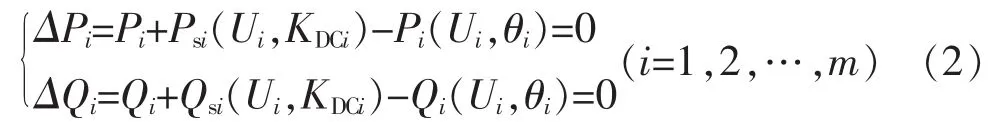
式中：Psi（Ui，KDCi）是第i個VSC注入交流母線的有功功率；Qsi（Ui，KDCi）是第i個VSC注入交流母線的無功功率。Ui是交流母線電壓，KDCi是直流系統變量

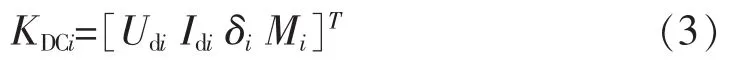
式中：Udi表示VSC換流器直流電壓；Idi表示VSC換流器直流電流；δi表示PWM控制器相位角；Mi為PWM控制器調制度。

由式（1）和式（2）組成了AC/VSC-HVDC混聯系統的交流系統穩態數學模型

式中：U為交流系統節點電壓，θ為相角。

1.2 AC/VSC-HVDC系統直流子系統穩態數學模型

VSC注入交流系統第i個節點的有功功率Psi和無功功率Qsi可以表示為［10］

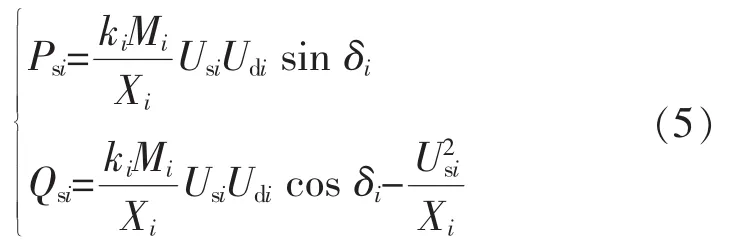
式中：k為VSC的直流電壓利用率（0＜ki＜1）；M為VSC的調制度；Us為與VSC換流器相連的交流節點的電壓基波分量；Ud為VSC直流側的直流額定電壓；X為與VSC連接的換流電抗器電抗。

由式（5）可以得到VSC節點交流系統側的功率偏差方程

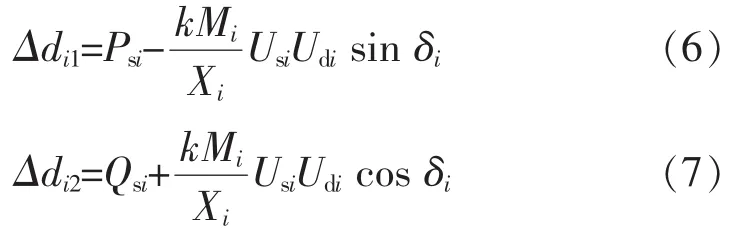
忽略VSC控制器內阻，則直流系統功率Pdi與VSC直流系統側的有功功率Pci相等

進而得到VSC輸出端節點功率偏差方程

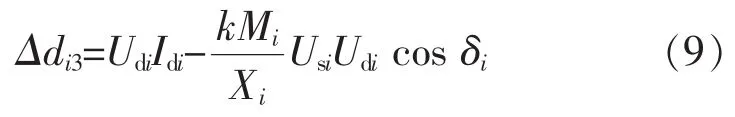
再由直流網絡列出節點電壓方程

式中，G表示直流子系統的節點導納矩陣。

得到第4個偏差方程

令式（6）、（7）、（9）、（11）偏差均為零，便是求解直流系統變量的數學方程，概括寫為

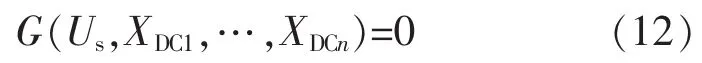
由式（12）得到牛頓法修正方程的矩陣形式

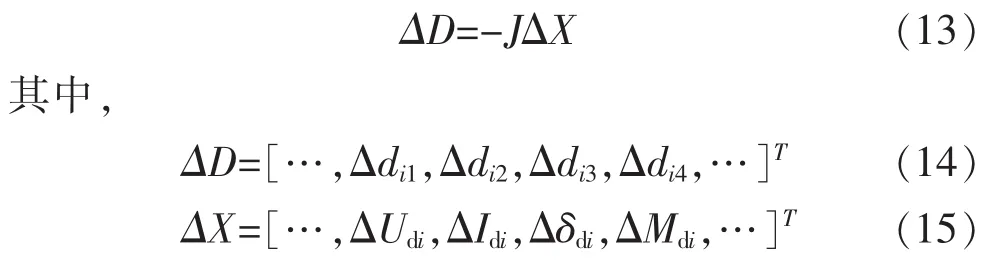
2 AC/VSC-HVDC混聯系統靜態電壓穩定分析方法

延拓法有4個基本環節：參數化環節、步長控制、預估環節和校正環節。P-V曲線常被用來分析電力系統的電壓穩定性。在交流系統模型中引入負荷增長水平參數λ，用來反映系統中負荷PL和發電機功率PG的變化，則穩態模型變為包含參數λ的擴展方程。參數化后的負荷和發電機功率可統一表示為

式中：Yd表示發電機功率和負荷功率的增量；Y0表示發電機功率和負荷功率的初始值；Ys表示當前的發電機功率和負荷功率。

引入負荷增長水平參數λ后，式（4）變為

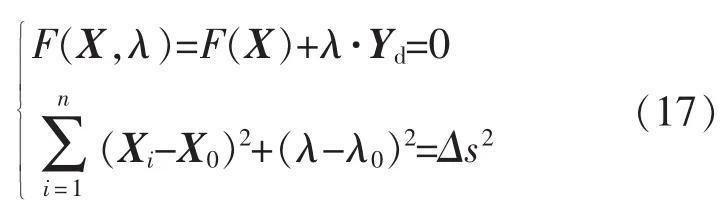
式中：λ0是P-V曲線上一個穩態點的負荷增長水平參數；Δs為延拓法中定義的弧長。X為系統中節點電壓的幅值和相角向量。

文獻［11］指出在描述交流系統的非線性代數方程中包含有與直流系統相關的變量，因而需要增加描述直流系統的方程式。對這樣的混聯系統進行分析計算時不能沿用原來的純交流方法，通常采用交替求解法或統一迭代法進行求解。

確定交直流迭代步驟后，就可以用交替求解法結合延拓法進行求取聯合系統的電壓崩潰點。每一次交直流迭代收斂之后，都作為P-V曲線上的一個穩定點，然后用延拓法預估下一個可能的穩定點并校正得到精確點，如此反復，最終得到系統的電壓崩潰點。

3 算例分析

計算流程如圖1所示。

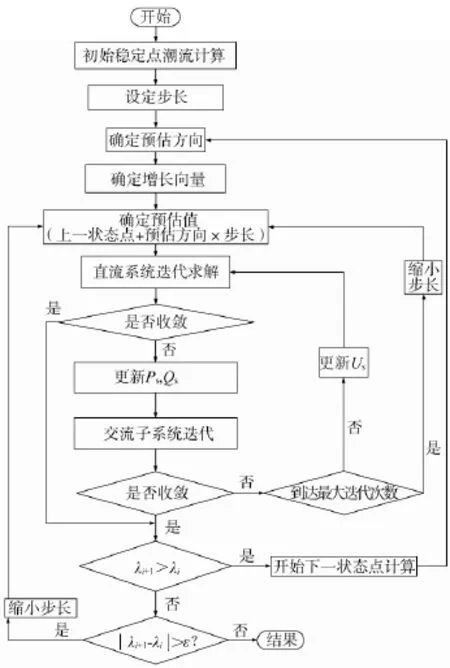
圖1 計算流程

考慮到現實情況下，發電機所發有功和無功數值有限，因此，在電力系統靜態電壓穩定性分析中必須考慮發電機的有功和無功功率輸出約束［12］。如果系統中存在多個發電機，那么，在延拓計算過程中，要盡量使每個狀態點相對于上一狀態點只有一個限制達到條件并起作用，否則將有可能導致臨界點的計算失真。

算例采用新英格蘭10機39節點系統，假定在節點10、12以及節點14間通過直流線路連接，彼此互聯構成三端直流網絡，則與其它交流系統部分共同組成了AC/VSC-MVDC系統。取增長方式Yd=Y0，計算精度ε=1.0×10-5，發電機功率限制見表1。

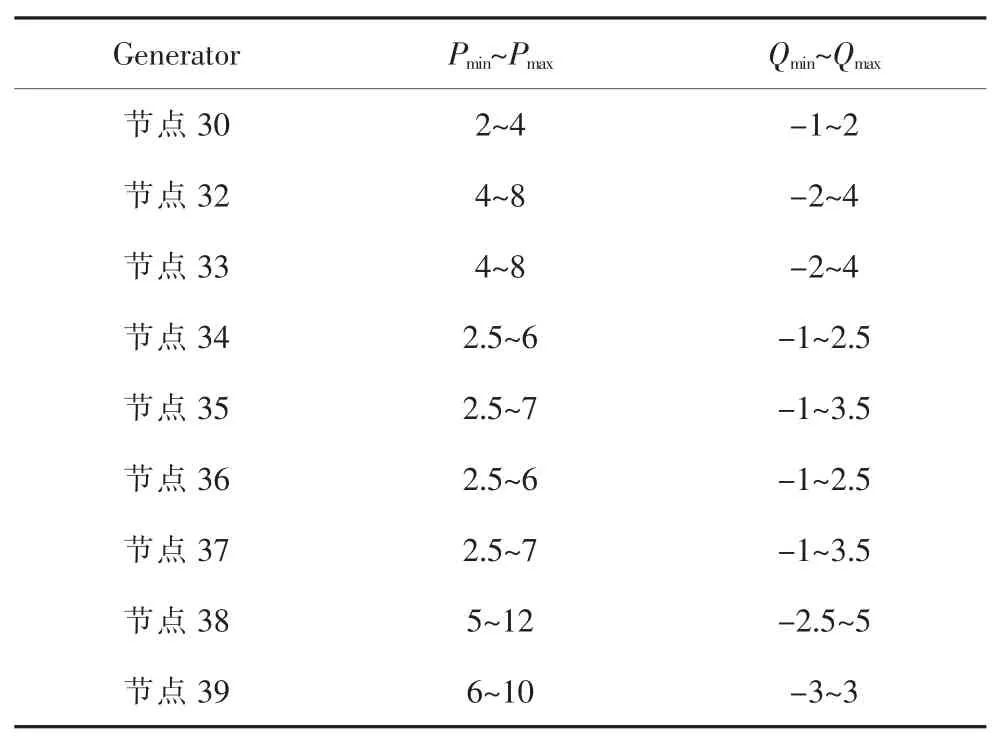
表1 發電機功率限制

VSC初始控制方式如表2所示。

表2 VSC初始控制方式

VSC控制器的設定參數及控制器限制見表3、表4。

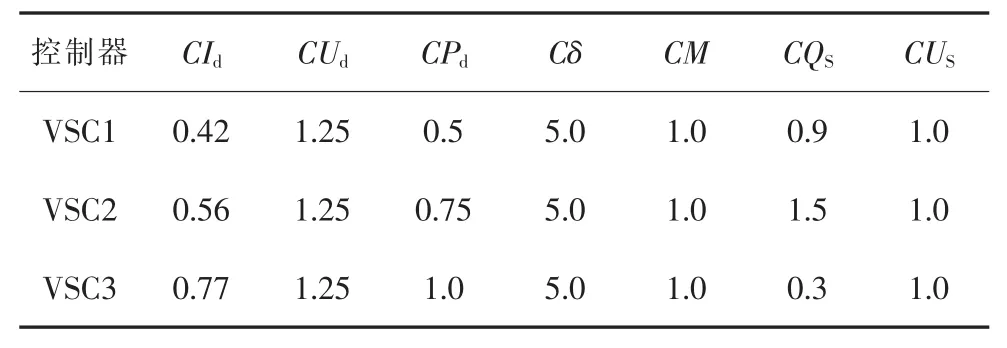
表3 VSC設定參數限制

表4 VSC控制器限制

AC/VSC-MTDC初始狀態點的計算結果見表5。

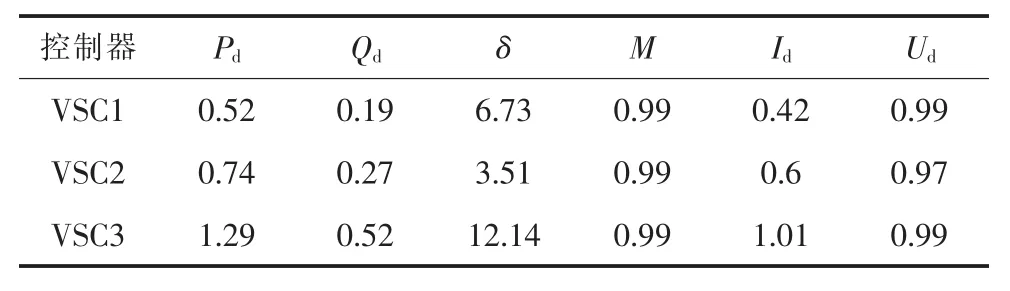
表5 初始運行點計算結果（λ=0）

不考慮發電機有功和無功功率限制情況下，AC／VSC-MTDC系統的崩潰點計算結果見表6。

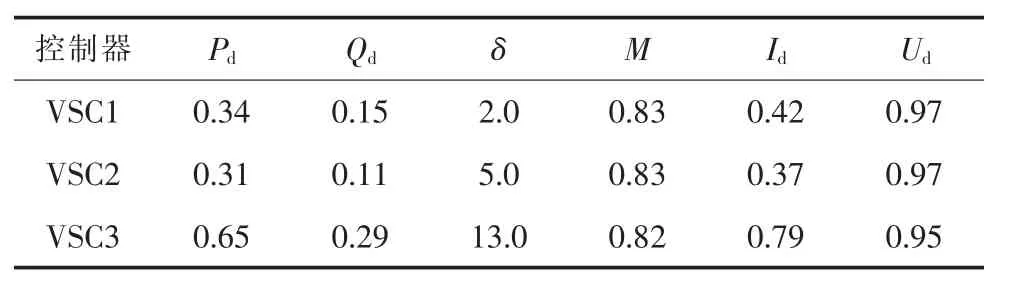
表6 不考慮發電機功率限制時崩潰點計算（λ=1.12）

考慮發電機有功和無功限制情況下，AC/VSCMTDC系統的崩潰點計算結果見表7。

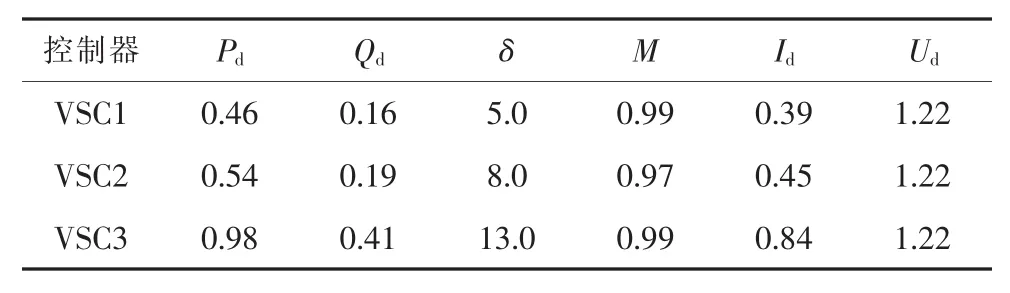
表7 考慮發電機功率限制時崩潰點計算（λ=0.41）

由以上算例驗證了提出的靜態電壓穩定分析算法的實用性，能夠用于AC/VSC-MTDC系統。表6與表7的結果表明：當不考慮發電機無功約束時，系統電壓崩潰點對應的功率增長因子λ=1.12；若考慮發電機無功約束，則λ=0.41，崩潰點位置遠小于前者，表明在AC/VSC-MTDC系統的靜態電壓穩定中，無功功率同樣對系統穩定起著重要作用，系統在無功功率充足情況下才能夠保持穩定運行。

4 結語

本文結合延拓法和交替求解法的原理提出了一種AC／VSC－HVDC混聯系統靜態電壓穩定分析方法，將交流迭代與直流迭代分別進行，可方便考慮發電機出力的上下限以及VSC-HVDC的運行方式轉換等問題，并通過算例將此方法應用于AC／VSCMTDC混聯系統的靜態電壓穩定性分析，得知該方法的有效性和可行性。

［1］丁道齊.現代電網的發展與安全［M］.北京：中國電力出版社，2012.

［2］Xiao Wang，Ooi B.T.High Voltage Direct Current Transmission System based on Voltage Source Converters.PESC’90 Record，SanAntonio，Texas，USA.1990（1）：325-332.

［3］陳謙，唐國慶，胡銘.采用dq0坐標的VSC-HVDC穩態模型與控制器設計［J］.電力系統自動化，2004，28（16）：61-66.

［4］李國棟，毛承雄，陸繼明，等.基于逆系統理論的VSC-HVDC新型控制［J］.高電壓技術，2005，31（8）：45-50.

［5］Durrant.M，Werner.H，Abbott.K.Model of a VSC HVDC Tenmnal Attached to a Weak AC System.Proceedings of 2003 IEEE Confereneeon Control Applications，Istanbul.2003：178-182.

［6］D.Jovcic，L.A.Lamont L.Xu.VSC Transmission Model for Analytical Studies.IEEE Power Engineering Society General［7］Meeting. 2003，7.

［8］張桂斌，徐政，王廣柱.基于VSC的直流輸電系統的穩態建模及其非線性控制［J］.中國電機工程學報，2002，22（1）：1-5.

［9］陳謙.新型多端直流輸電系統的運行與控制［D］.南京：東南大學，2004.

［10］Guangkai Li，Guopeng Ma，Chengyong Zhao，et al.Research of Nonlinera Control Strategy for VSC-HVDC System Based on Lyapunov Stability Theory.Electric Utility Deregulation and Restructuring and Power Technologies，2008.

［11］陳謙，唐國慶，王潯.多端VSC-HVDC系統交直流潮流計算［J］.電力自動化設備，2005，25（6）：1-6.

［12］趙成勇，李金豐，李廣凱.基于有功和無功獨立調節的VSCHVDC控制策略［J］.電力系統自動化，2005，29（5）：20-24，30.

［13］姜志勇.AC/MTDC系統靜態電壓穩定性分析［D］.哈爾濱：哈爾濱工業大學，2009.

［14］王晶芳，李新年，胡濤，等.含特高壓直流的多饋入交直流系統動態特性仿真［J］.電力系統自動化，2007，31（11）：97-102.

Study on the Static Voltage Stability of AC／HVDC Hybrid Power System Based on VSC

Large regional power grid using asynchronous interconnection is the future trend of the grid.HVDC technology is a key technology to implement asynchronous interconnection.VSC-HVDC transmission technology is one of the main development directions of HVDC technology.It is different from the more mature and traditional PCC and CSC technology，there is few study of static voltage stability problems based on AC/VSC-HVDC system.So this paper has a more in-depth discussion with this problem，proposed an AC/VSC-HVDC power system static voltage stability analysis method.The feasibility of the algorithm，is confirmed by examples.

static voltage stability；VSC-HVDC；AC/HVDC hybrid power system

TM721.3

：A

：1007－9904（2014）03－0013－04

2014-02-07

毛志強（1988—），男，工程師，從事電力系統運行與控制工作。