基于非對稱模糊PI控制的光伏發電MPPT研究

楊海柱，劉 潔，曾志偉，姚君旺

（1.河南理工大學電氣工程與自動化學院，河南焦作 454000；2.河南理工大學計算機科學與技術學院，河南焦作 454000；3.六盤水師范學院 物理與電子科學系,貴州六盤水 553004）

光伏發電具有無污染、無噪音等優點，越來越受到關注。制約光伏發電系統發展的主要因素是能量轉換效率問題，所以提高光伏陣列的光電轉換效率并使其輸出功率最大化，即在理論和實踐上提出了光伏陣列的最大功率點跟蹤問題。由于傳統方法的局限性，本論文采用智能控制方法的智能性、自適應性來對非線性光伏發電系統進行控制，無疑是一個很好的選擇[1]。

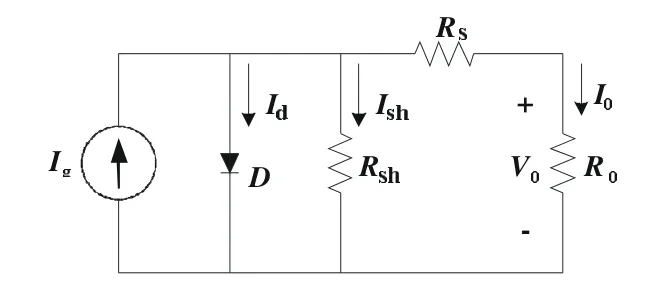
圖1 太陽電池等效電路

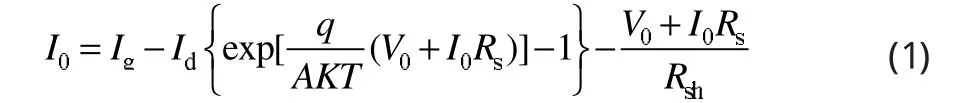
1 太陽電池陣列特性

太陽電池是一種光電轉換的半導體裝置，其產生的電壓和電流分別受溫度和光照強度的影響。當受光照射的太陽電池接上負載時，光生電流流經負載，并在負載兩端建立起端電壓。這時太陽電池的工作情況可用圖1所示的等效電路來描述。

當流進負載R0的電流為I0，負載的端電壓為V0時，由太陽電池的等效電路圖可以得到如下的解析式：

式中：Ig為光生電流；Id為二極管飽和電流；q為電荷電量 (1×10－19C)；A為二極管因子；K為波爾茲曼常數 (1.38×10－23焦耳/度)；T為開氏溫度(K)；V0為電池的輸出電壓；I0為電池的輸出電流；Rs為等效串聯電阻；Rsh為等效并聯電阻。

根據光伏電池等效電路圖建立其仿真模型，調節電阻負載的大小進行采樣，當光照變化時光伏陣列的I-V特性曲線和P-V特性曲線如圖2所示[2]。從圖中可以看出在溫度不變的條件下，光伏電池的開路電壓隨光照的降低而下降，短路電流和光照成正比，最大輸出功率隨光照的升高而劇增。

2 基于非對稱模糊PI控制原理及實現

常用的最大功率跟蹤控制算法有恒電壓跟蹤算法(CVT)、干擾觀察法(P&O)、增量電導法(IC)等。對于那些時變的、非線性的復雜系統，當無法獲得精確的數學模型時，利用具有智能特性的模糊控制器能給出有效的控制[3-5]。

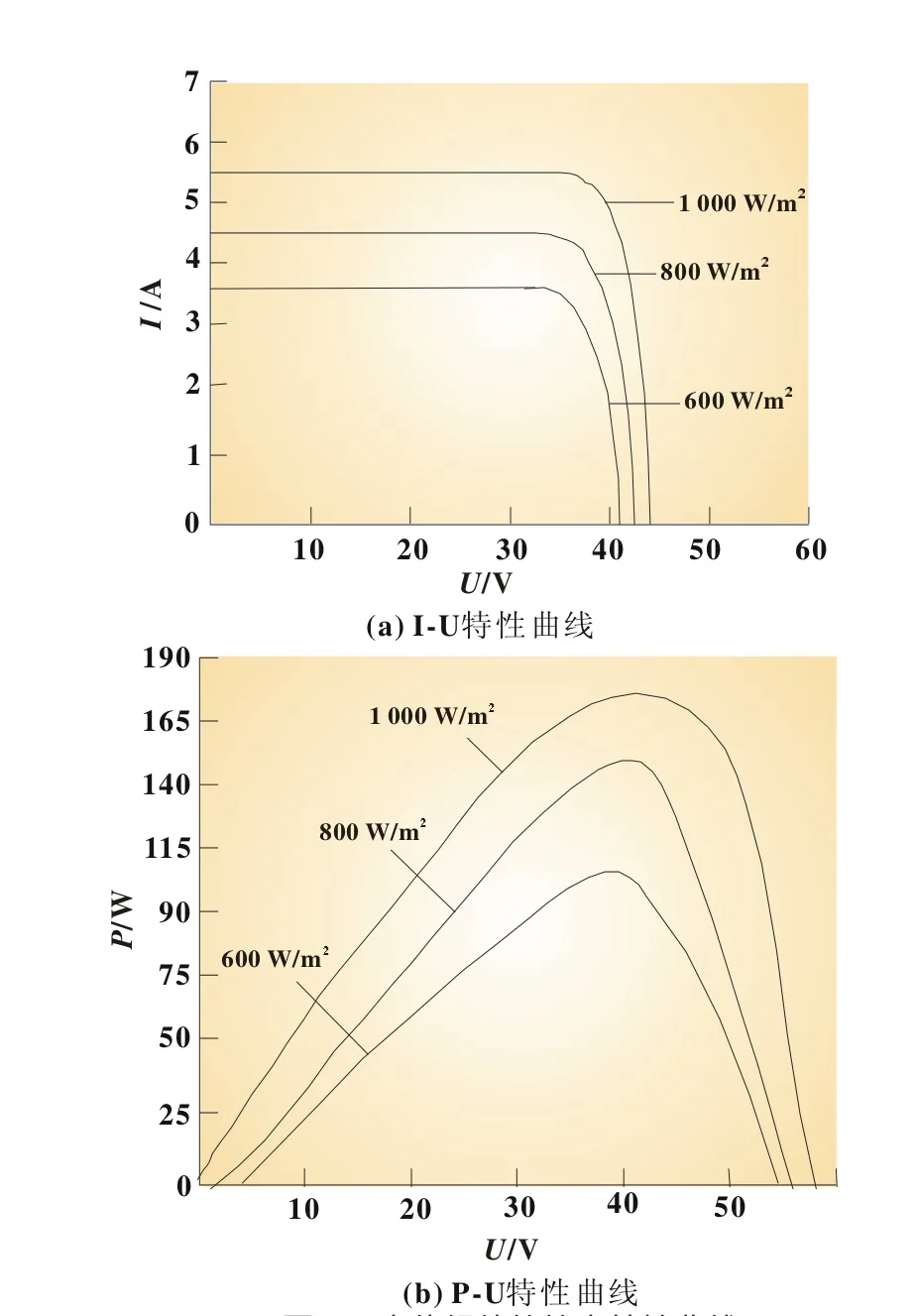
圖2 光伏組件的輸出特性曲線

光伏電池輸出功率見公式(2)，公式(3)是輸出功率對輸出電壓的導數d P/d V，表明該導數是輸出電壓的單調函數。當輸出電壓為零時該值最大，大小等于電池的短路電流；隨著輸出電壓的增加，d P/d V緩慢下降，在輸出功率最大點附近該值下降速度加快，在MPP點該值等于零；隨著輸出電壓V進一步增加，d P/d V變為負值，絕對值快速上升遠大于曲線在最大功率點左側的值，特性曲線見圖3。公式(2)和圖3表明最大功率點兩側相同電壓變化△V造成的功率變化有很大差異，因此在最大功率點兩側應該采用不同的占空比△d，實現光伏電池最大功率跟蹤。

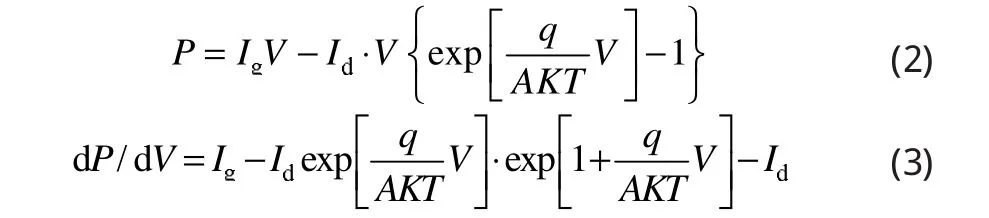
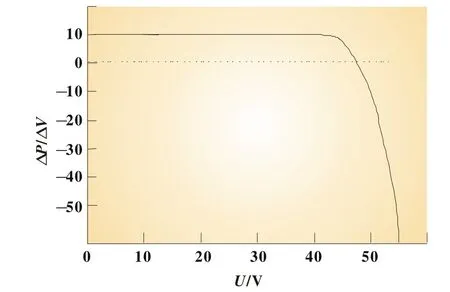
圖3 光伏電池d P/d V-V特性曲線

因此根據光伏電池的特性將非對稱模糊-PI控制應用到光伏電池的最大功率點跟蹤，它在最大功率點兩側采用不同的控制策略和隸屬度函數，可以有效消除功率振蕩現象。本文提出的非對稱模糊PI控制系統如圖4所示[6]。

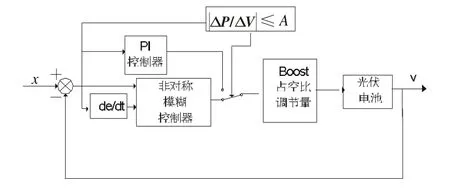
圖4 非對稱模糊PI控制原理圖

2.1 非對稱模糊控制器的設計

2.1.1 模糊控制器的輸入量和輸出量

模糊控制器兩個輸入分別是誤差e和誤差變化ec，見公式(4)。輸出為MPPT電路中開關器件占空比的改變量△d。

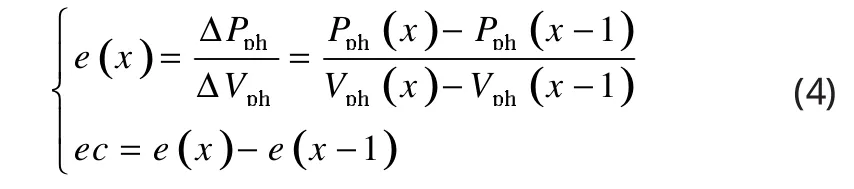
2.1.2 量化因子和比例因子

為便于控制，分別對誤差e和誤差變化ec的實際值進行量化，用比例因子把模糊控制器的輸出轉化為MPPT電路開關占空比的變化量△d，然后映射到模糊集合論域Ep和Ed。

e，ec的論域均為{－0.5,0.5}，△d的論域為{－0.01，0.01}

2.1.3 隸屬度函數

根據光伏電池的特點，本文誤差選用非對稱的隸屬度函數，為了便于實現和保證系統可靠運行，輸出采用梯形隸屬度函數，如圖5所示。

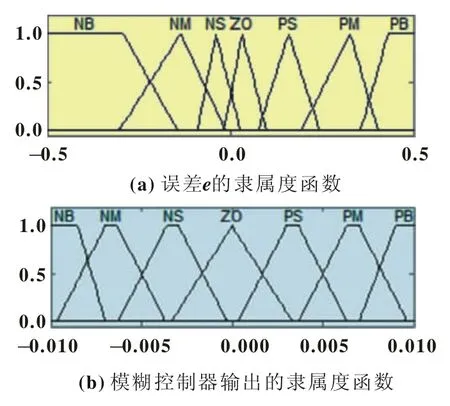
圖5 隸屬度函數

2.1.4 模糊決策表和解模糊方法

選取控制量的原則：當誤差大或較大時，選擇控制量以盡快消除誤差為主；當誤差較小時，選擇控制量要注意防止超調，以系統穩定性為主要出發點。確定了輸入和輸出控制量之后，下一步是設計模糊控制器的控制規則。在本方案中，模糊推理采用Mamdani方式，解模糊方法為面積重心法。最后得到模糊規則表，如表1所示。

2.2 非對稱模糊-PI控制仿真圖

通過Matlab的Fuzzy Logic工具箱可以建立模糊子系統。采用非對稱模糊控制算法通過占空比來調整最大輸出電壓的同時，需要考慮占空比的步長，步長過大，精度達不到要求，穩態誤差變大；步長過小，跟蹤時間過長，易在MPP點附近反復振蕩，為了最終達到自動尋優的效果。設計了非對稱模糊-PI系統，其仿真圖如圖6所示。根據論域和變量實際取值范圍，e和ec的比例因子都為0.1，△d的比例因子為10，根據經驗，|△P/△V|≤A中，A取 0.06，仿真時間設置為 0.01 s，延時時間為0.000 02 s。通過多次仿真實驗得出，當比例系數kp=0.01，ki=1時，PI控制器能夠達到較好的控制效果[7]。

3 仿真結果分析

設定初始條件：以NT-R5E3E 175W太陽電池板為仿真目標；G=1 000W/m2，T=25℃。采用占空比擾動法和非對稱模糊控制法的功率輸出曲線如圖7和圖8所示。從圖7中可以看出，系統從初始功率0W上升到功率175W，并在0.01 s左右達到穩定狀態，并伴隨有較大功率振蕩；在t=0.1 s時，當光強突變到G=800W/m2，系統在0.11 s左右達到最大功率點并穩定于140W左右。從圖8可以看出，加入模糊控制之后，響應速度明顯加快了，最大功率點處功率振蕩明顯減少。非對稱模糊-PI控制的輸出功率跟蹤曲線如圖9所示。通過仿真對比發現，都能跟蹤系統最大功率點，占空比擾動法響應速度慢，適合光照強度變化緩慢的場合，并且在穩態情況下，會導致光伏電池的實際工作點在MPP點的附近振蕩。加入非對稱模糊-PI控制之后，能夠有效地提高動態系統特性和精度，快速跟蹤最大功率點，消除最大功率點處功率振蕩，穩定性好。

圖7 功率輸出

圖8 功率輸出

圖9 功率輸出

4 結論

本文針對光伏電池的非線性特性曲線，以及傳統最大功率點跟蹤方法的不足，應用智能、自適應性控制方法，將非對稱模糊-PI控制應用于光伏電池MPPT中。通過仿真驗證：該方法在外界環境變化劇烈的情況下，快速跟蹤光伏電池的最大功率點同時能基本消除最大功率點的功率振蕩現象，具有較高的控制精度和穩定性。

[1]沈輝,曾祖勤.太陽能光伏發電技術[M].北京:化學工業出版社，2005.

[2]茆美芹,余世杰,蘇建徽.帶有MPPT功能的光伏陣列Matlab通用仿真模型[J].系統仿真學報，2005,17(5):1248-1251.

[3]蘇義鑫，向爐陽，張丹紅.基于改進擾動法的光伏電池MPPT仿真研究[J].武漢理工大學學報，2012(4)：135-139.

[4]XIAOWD,DUNFORD WG.A modified adaptive hill climbing MPPT method for photovoltaic systems[C]//35th annual IEEE Power Electronic Specialists Conference.Germany,IEEE：2004,1957-1963.

[5]TAFTICHT T,AGBOSSOU K.Developmentof aMPPTmethod for photovoltaic systems[C]//Electrical and Computer Engineering,2004 Canadian Conference.Canada,Electrical and Computer Engineering：2004,5(2):1123-1126.

[6]SIMOESMG,FRANCESCHETTIN,FRIEDHOFERM.Fuzzy logic based photovoltaic peak power tracking control[C]//Proc IEEE Conf International Symposium on Industrial Electronics.Pretoria：IEEE，1998,300-305.

[7]張超,何湘寧.非對稱模糊PID控制在光伏MPPT中的應用[J].電工技術學報，2005,20(10):72-75.