上海市高速公路交通量影響因素分析

劉 令,田 健,焦 丹

（1.吉林建筑大學，長春 130118；2.華茂外國語學校，浙江 寧波 315192）

上海市高速公路交通量影響因素分析

劉 令1,田 健1,焦 丹2

（1.吉林建筑大學，長春 130118；2.華茂外國語學校，浙江 寧波 315192）

高速公路交通量（道路上行駛的各類車輛的車流量）的大小反應了社會經濟發展對高速公路的交通需求。本文將影響上海市交通量的因素歸納為社會經濟類、交通設施類和公共政策類三大類，并逐層細化。運用聚類分析對交通量（即因變量）進行歸納，使用相關性分析對影響因素（即自變量）進行篩選。采用一元線性回歸和彈性回歸模型研究了人均GDP對不同類別交通量的影響程度，并對比分析了各個模型的優劣。

人均GDP因子；一元線性回歸模型；彈性回歸模型

0 引言

高速公路交通量反應了社會經濟發展對高速公路的交通需求。2003-2011年上海市高速公路交通量呈線性增長趨勢，年均增長超過5萬輛/日。為了把握上海市高速公路交通量的發展趨勢，本文通過對交通量的因子分析，利用一元線性回歸和彈性回歸模型建立了人均GDP與交通量的關系，為未來高速公路的發展定位和經濟評價提供了有力的依據。

1 確立交通量影響因素

社會經濟類因素可以分為7類，分別為：人均GDP、工業總產值、固定資產投資值（以貨幣表現的建造和購置固定資產 活動的工作量）、社會消費品、人口數量、車流量、港口貨物吞吐量（由水運進出港區并經過裝卸的貨物數量，吞吐量分為進口、出口）；交通設施類因素包括道路容量（道路的流量承載限度）；公共政策類因素包括2003、2004年調整公路車輛通行費的車輛分類標準，2006年起對A30環郊的彈性收費，2009年起對A12（滬嘉高速）的客車彈性收費。

聯系實際，通過對政策實施前后高速公路網的流量比較分析發現，上述3種政策的影響很小，因此，本文分析時未作為自變量輸入。由于自變量個數過多，本文主要考慮人均GDP的影響狀況，從而，結合2002-2011年自變量和因變量的相關數據[1]進行模型的建立與分析。

2 模型建立與分析

2.1 一元線性回歸模型

在本文回歸分析模型中，將因變量分為高速公路總流量、上海市域內總流量和進出上海的總流量三類進行。一元線性回歸模型可以反應一個因變量與自變量之間的線性關系，其模型[2]可以表示為：

式（1）中，β2是y和x關系式中的斜率參數，β1為常數項。

人均GDP對高速公路總流量（y1）、上海市域交通量（y2）和進出上海的總流量（y3）三類流量均是非常重要的解釋變量，三類流量的一元線性回歸估計模型整理如下：

y1=10.75527x-271313

y2=6.95541x-177707

y3=3.79987x-93607.

2.2 彈性回歸模型

彈性模型又稱為對數值-對數值模型，其參變量與一元線性回歸模型一致。其函數形式[3]為：

式（2）中，γ1為彈性系數（y指標變化的百分率/x 指標變化的百分率）。

根據對未來經濟發展趨勢的估計確定P（x）（人均GDP的增長率），計算P（m）（高速公路流量的趨勢增長率）：

P（m1）=γ1P（x）

所以未來第n年的交通流量預測值為：

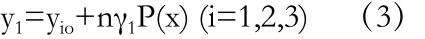
式（2）、（3）中，yio為初始年交通量：y10表示高速公路初始年總流量，y20表示上海市域初始年交通量，y30表示進出上海的初始年總流量。

人均GDP對三類流量均是非常重要的因素，三類流量的彈性回歸的估計模型整理如下：三類流量的增長率具體如下：

P（m1）=2.0345P（x）

P（m2）=1.99972P（x）

P（m3）=2.0798P（x）

三類流量未來第 年的交通流量預測如下：

y1=y10+2.0345nP（x）

y2=y20+1.99972nP（x）

y3=y30+2.0798nP（x）

3 誤差分析

利用估計參數[4]（總體中抽取的樣本估計總體分布中包含的未知參數的方法）對線性模型回歸及彈性模型回歸的結果進行評價，對比估計值與實際值之間的絕對誤差和相對誤差，并對三類流量的模型進行誤差分析，得知彈性模型的絕對誤差要大于線性模型，進而彈性模型可以更好地反映經濟增長對高速公路流量的影響；對于相對誤差，兩種模型對高速公路總流量的估計誤差分別為2.5％和6.4％，而市域流量和進出流量的估計誤差相對較大，可以看出兩種模型對高速公路總流量的估計精度要大于對市域流量和進出流量的估計精度。

4 結語

本文對影響上海市高速公路交通流量的人均GDP因子進行深入分析，運用一元線性回歸和彈性回歸模型，為發現上海市高速公路流量的歷史變化規律及預測未來發展趨勢提供了有力依據。同時經過對兩個模型的誤差分析，得出在經濟形勢穩定的情況下，采用線性回歸模型進行對未來高速公路流量的預測，精度相對更高；而在經濟形勢波動時，彈性模型的估計和預測結果要優于線性模型。總體來說，對模型的誤差分析增強了本文的說服性，進而完備了分析方案，更有利于實現對不同類相關問題的分析與解決。

[1]上海市統計局[Z].上海市統計年鑒,2002-2011年

[2]王松桂.線性統計模型[J].高等教育出版社 2004（07）.

[3]康德英.彈性系數計量回歸模型及其分析[J].中國衛生經濟,1996（03）.

[4]張金槐.線性模型參數估計及其改進[J].國防科技大學出版社2000（09）.

劉令（1982—），女，吉林長春人，博士，主要研究偏微分方程。