基于IMM-MHT算法的雜波環境多機動目標跟蹤

邵俊偉，同 偉，單 奇

（1.中國電子科技集團公司第38研究所，合肥 230088；2.陸軍駐中電集團38所軍事代表室，合肥 230088）

0 引 言

隨著戰場環境的日趨復雜以及目標機動性能的日益提升，如何在雜波環境下跟蹤機動目標正成為雷達數據處理系統要應對的關鍵問題之一。傳統數據關聯算法，如最近鄰［1］（NN）、概率數據關聯［2］（PDA）、聯合概率數據關聯［3］（JPDA）等，以當前掃描周期內的量測為基礎進行數據關聯，若某一掃描周期內的關聯結果與真實情況有較大差別，則之后的跟蹤過程常會發生錯誤，甚至丟失目標。多假設跟蹤［4］（MHT）的關聯結果不僅取決于當前掃描周期內的量測數據，而且還與歷史量測信息有關。對不能確定的關聯，會形成多種邏輯假設，并用后續的量測數據來解決這種不確定性。在理想條件下，MHT是最優的數據關聯算法，可以有效地解決雜波環境下的數據關聯問題。但是，MHT算法所需的計算和存儲資源會隨著量測數和跟蹤步數的增長呈指數增加，若要實際應用，還需要有效的假設管理技術。

對機動目標，以單一的運動模型來刻畫其運動過程，往往和實際情況有偏差，最終會由于模型失配導致跟蹤誤差增大甚至跟蹤失敗。交互多模型［5］（IMM）算法使用多種運動模型對目標進行跟蹤，模型間的轉換服從已知轉移概率的有限Markov過程。在跟蹤過程中對各模型的概率進行更新，可以起到自適應調整模型的作用，得到較好的跟蹤效果。

本文將IMM跟蹤算法與MHT關聯算法結合起來，并采用文獻［6］在解決視頻跟蹤問題時所用的MHT假設生成和假設管理技術，來實現雜波環境下對多機動目標的跟蹤。仿真結果驗證了此方法的有效性。

1 算法描述

1.1 MHT算法原理

1979年Reid［4］針對多目標跟蹤問題，基于“全鄰”最優濾波器和Bar-Shalom的聚概念，提出了MHT方法。此算法的執行可以分為假設生成、假設概率計算和假設管理3個步驟。

1.1.1 假設生成

記Ωk為直到k時刻的關聯假設集合，Zk＝｛zk，1，…，zk，mk｝為k時刻的量測集合；Zk為直到k時刻的累積量測集合。Ωk由直到k-1時刻的關聯假設集Ωk-1和當前量測集Zk關聯得到，規定每個目標至多與一個落入跟蹤門內的當前量測關聯。

若每條假設航跡與落入跟蹤門內的所有量測都進行關聯，則生成的假設航跡數量會隨目標和量測數目的增加而急劇增長，無法滿足實時跟蹤的需求。利用Murty算法，可以在不生成所有假設的條件下，得到前M個概率最大的關聯［6］。先構造1個分配矩陣，行對應量測，列對應目標、雜波或新目標，矩陣的元素是量測來自于相應目標的負對數概率，或是量測來自于雜波或新目標的負對數概率，這樣前M個概率最大的關聯，即是該分配矩陣前M個費用最小的分配，而后者可以通過Murty算法求解［7］。

1.1.2 假設概率計算

記θk為k時刻量測與目標的關聯事件，該事件中τ個量測源于已建立航跡，v個量測源于新目標，ψ個量測源于虛警。引入如下記號：

設Θk，l表示關聯假設集Ωk中的第l個假設，由假設生成的概念，它由Ωk-1中的某個假設Θk-1，s和關聯事件θk組合得到，即Θk，l＝ ｛Θk-1，s，θk｝ 。利用Bayes公式，可以得到假設Θk，l的后驗概率［8］：

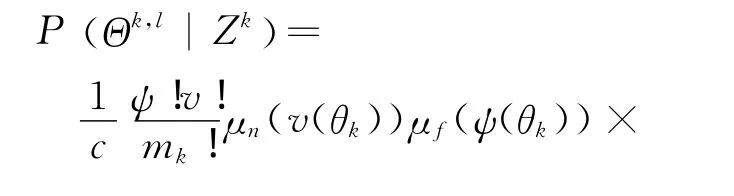
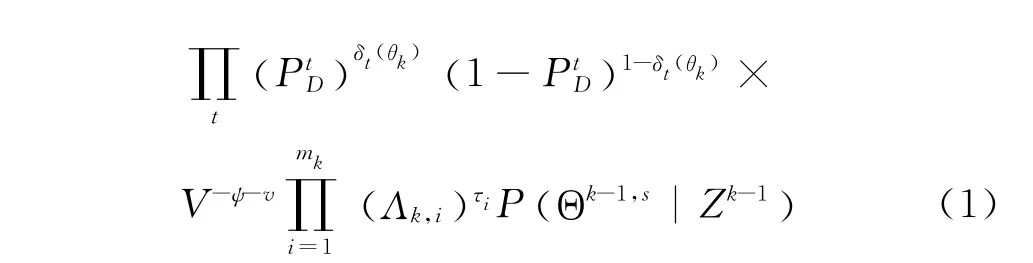
在缺乏先驗知識的情況下，一般可假定虛警和新目標在跟蹤門內服從均勻分布，新息服從Gauss分布，而虛警和新目標的數目服從Poisson分布。

1.1.3 假設管理

隨著跟蹤步數的增加，關聯假設的個數會呈指數增長。為提高MHT算法的執行效率，可以使用如圖1所示的假設樹來進行關聯假設的管理［6］。

圖1 MHT假設樹

該假設樹通過以下2個參數對關聯假設進行管理：

（1）非葉子結點的子結點數M：表示前一時刻的假設集Ωk-1中的每個關聯假設Θk-1，s，在與當前時刻的量測集Zk進行關聯時，僅保留前M個概率最大的關聯假設。

（2）樹的深度N：表示只記錄最新N個掃描周期內的關聯假設信息。

每步生成新的關聯假設后，選取所有MN個當前關聯假設（在假設樹的第N＋1層）中概率最大的一個，保留以其第2層父結點為根結點的子樹，并刪除其他結點，維持整棵假設樹的深度為N。假設樹剪枝后，葉子結點共有MN-1個，對應了k時刻的假設，而唯一的根結點對應了k-N＋1時刻的唯一假設，因此，在k時刻可以將根結點對應的估計輸出，作為k-N＋1時刻關聯和跟蹤的結果。

1.2 IMM算法原理

1984年，Blom［5］在廣義偽Bayes算法的基礎上提出了一種具有Markov切換系數的多模型濾波器，其中多個模型并行工作，模型間基于一個Mark-ov鏈進行切換，目標狀態為多個濾波器交互作用的結果。IMM算法濾波的過程可以分為以下幾步：

（1）模型交互作用：

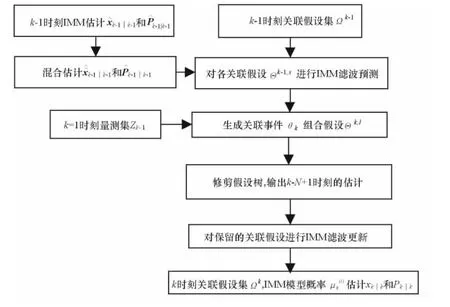
圖2 IMM-MHT單步關聯濾波流程

1.3 基于IMM的MHT算法

將IMM應用于MHT算法，單步關聯和濾波的過程如圖2所示。

2 仿真結果及分析

2個目標的初始狀態分別為：

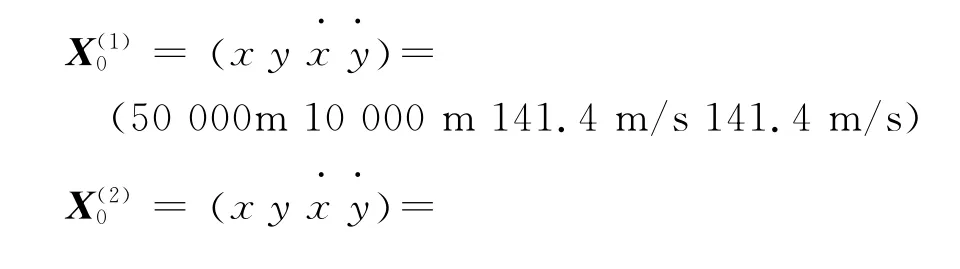
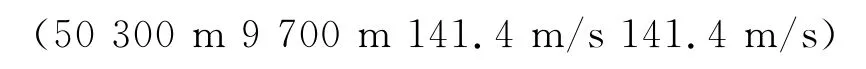
兩者保持恒定速率運動，先沿直線運動20s，再向右以18°／s的角速度作勻速轉彎運動10s，再沿直線運動10s，再向左以18°／s的角速度作勻速轉彎運動10s，最后再沿直線運動20s。雷達的檢測概率為PD＝0.98，測距精度為σr＝100m，測角精度為σθ＝0.1°，采樣間隔為T＝1s，雜波密度為λc＝1e-7。

IMM模型集使用CV（勻速）模型和Singer模型［9］，模型的先驗概率為μ0＝ ［0.5，0.5］，Markov轉移概率矩陣為：

CV模型的過程噪聲取為q＝100。Singer模型的自相關時間常數為α＝1／10，最大加速度為aM＝70m／s2，最大加速度概率為pM＝0.1，非機動概率為p0＝0.7。量測方程使用線性模型，量測噪聲協方差由量測精度通過無偏量測轉換得到［8］。MHT假設樹參數為：M＝3，N＝3。

量測和真實航跡見圖3，基于IMM-MHT算法的跟蹤結果如圖4所示。

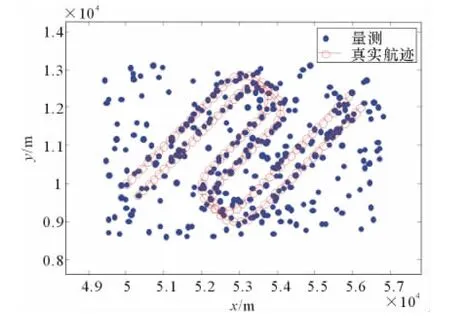
圖3 真實航跡及量測圖

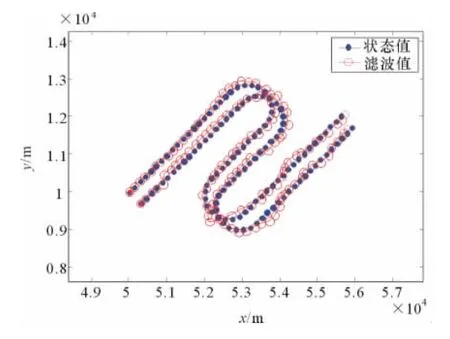
圖4 基于IMM-MHT的目標跟蹤

圖5是使用CV模型的關聯和跟蹤結果，圖6是使用Singer模型的關聯和跟蹤結果。可以看出，在目標發生機動時，CV-MHT算法容易跟蹤失敗；Singer-MHT算法和IMM-MHT算法在目標的機動段有類似的跟蹤性能，但對目標的直線段，前者跟蹤效果不如后者，而且前者容易導致關聯錯誤。

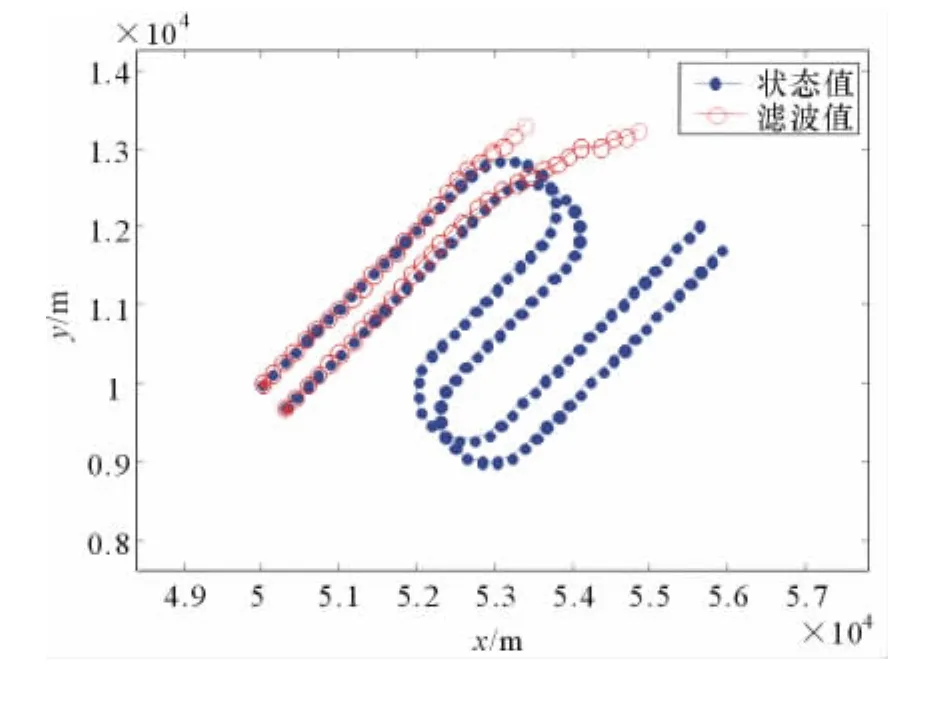
圖5 基于CV-MHT的目標跟蹤

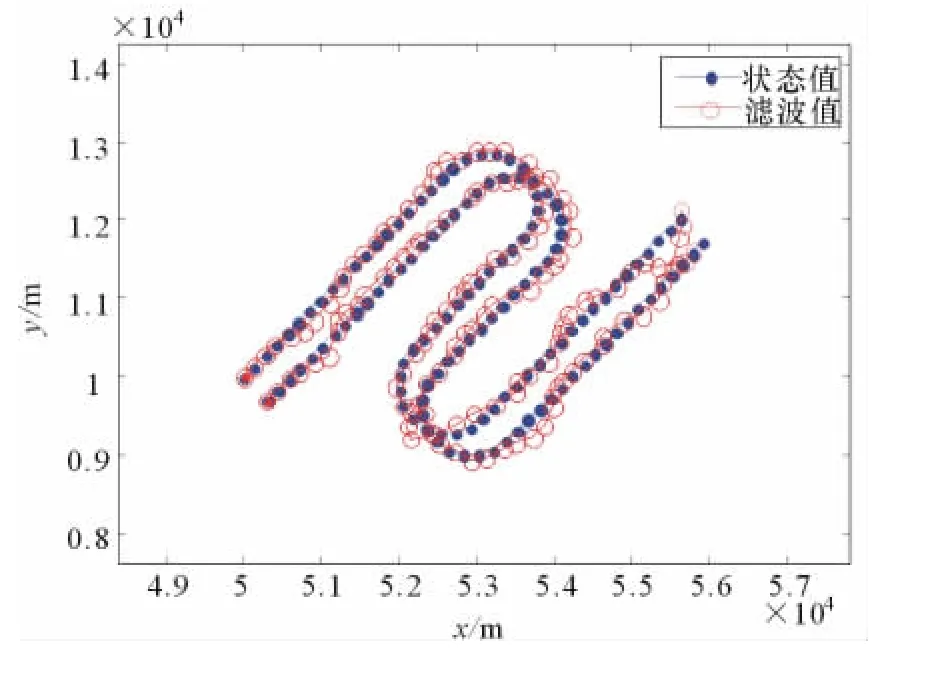
圖6 基于Singer-MHT的目標跟蹤

以相同的參數進行50次Monte Carlo仿真，跟蹤過程中目標丟失率、關聯錯誤率、跟蹤位置誤差均方根（RMSE）等結果如表1所示。

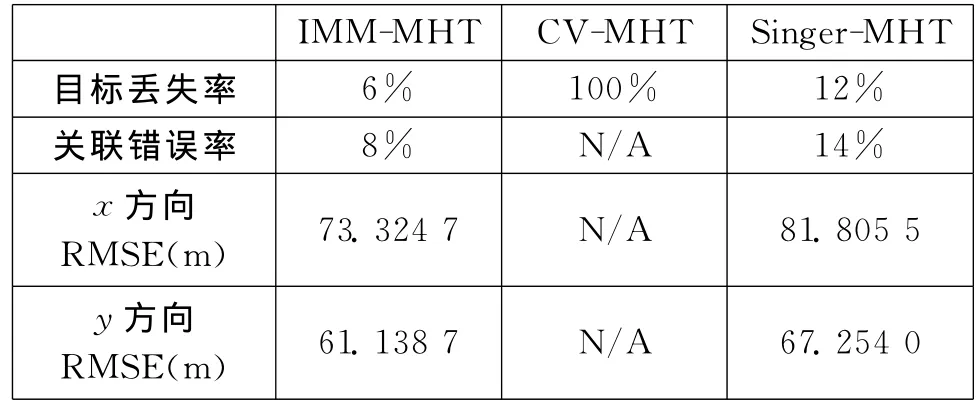
表1 50次仿真的跟蹤結果

3 結束語

本文將IMM濾波算法結合到MHT關聯算法中，并通過有效的MHT假設生成和假設管理技術，實現了雜波環境下對多機動目標的跟蹤，與只采用單模型的MHT算法相比，IMM-MHT算法具有更好的跟蹤穩定性和跟蹤精度，仿真結果表明了這一算法的有效性。

［1］ Singer R A，Sea R G.A new filter for optimal tracking in dense multitarget environment［A］.Proceedings of The Ninth Allerton Conference Circuit and System Theory［C］.Urbana，1971：201-211.

［2］ Bar-Shalom Y，Tse E.Tracking in a cluttered environment with probabilistic data association［J］.Automatica，1975，11（9）：451-460.

［3］ Formann T E，Bar-Shalom Y，Scheffe M.Sonar tracking of multiple targets using joint probabilistic data association［J］.IEEE Journal of Oceanic Engineering，1983，8（3）：173-183.

［4］ Reid D B.An algorithm for tracking multiple targets［J］.IEEE Transactions on Automatic Control，1979，24（6）：843-854.

［5］ Blom H A P.An efficient filter for abrupt changing systems［A］.Proceedings of The 23rd IEEE Conference on Decision and Control［C］，Las Vegas，1984：656-658.

［6］ Cox I J，Hingorani S L.An efficient implementation of Reid＇s multiple hypothesis tracking algorithm and its evaluation for the purpose of visual tracking［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1996，18（2）：138-150.

［7］ Murty K G.An algorithm for ranking all the assignments in order of increasing cost［J］.Operations Research，1968，16（3）：682-687.

［8］ 韓崇昭，朱洪艷，段戰勝.多源信息融合［M］.第2版.北京：清華大學出版社，2010.

［9］ 何友，修建娟，張晶煒，等.雷達數據處理［M］.第2版.北京：電子工業出版社，2009.