鍋爐與電廠管道系統應力分析關系探討

杜偉光，李 楊，程豐淵

（1.哈爾濱鍋爐廠有限責任公司，黑龍江 哈爾濱 150046；2.濟南鍋爐集團有限公司，山東 濟南 250023）

0 引言

在我國，鍋爐管道系統的應力分析和與之相連的電廠管道系統的應力分析是分別由鍋爐廠和電力設計院完成的。存在兩個計算系統在接口處的邊界條件的處理問題。 現行的做法是，鍋爐廠同時向設計院提出力的限制條件和位移條件，角位移為零，線位移為以鍋爐膨脹中心為零點計算的自由熱膨脹量，然后根據設計院反饋回來的力和力矩進行鍋爐管道系統的計算。

1 亞臨界鍋爐現行管道系統計算方法及問題

1.1 現行計算方法

亞臨界鍋爐現行管道系統計算方法是20世紀80年代初從美國CE公司引進的方法［1-2］。鍋爐制造廠先向設計院提供計算接口處的位移邊界條件和力的限制條件，鍋爐制造廠根據設計院反饋回來的力和力矩進行鍋爐系統的計算。

鍋爐廠向設計院提供的位移邊界條件：線位移△x、△y、△z，為以鍋爐膨脹中心為零點計算的自由熱膨脹量；角位移 θx、θy、θz，實際上應當根據計算接口處的結構形式和支撐情況確定，為了簡化并得到偏于安全的結果，一般規定θx=θy=θz=0。力的限制條件，根據經驗方法算出。

1.2 存在問題

從力學原理角度講，同時規定位移邊界條件和力的限制條件欠妥，因為這兩個條件設計院無法同時滿足。

鍋爐的全部自由熱膨脹量都讓電廠管道系統吸收欠妥。在電廠管道系統布置大體定型的情況下，設計院按這個位移邊界條件進行計算，一般會得到約束反力較大的結果。這樣，鍋爐管道系統設計和電廠管道系統設計都會偏于保守，因為雙方都加大了邊界約束。

如果追求滿足鍋爐廠提出的力的限制條件，設計院需要做多次的試算和結構調整，導致鍋爐廠提出的位移邊界條件就會自動打破。

2 改進的計算方法

2.1 聯合計算

鍋爐廠和設計院各派相關計算人員，共同對結構系統布置形式、構件的幾何參數和力學參數、各部位約束條件等情況進行統計計算和確認，建立統一的計算模型和評定標準。需要對結構布置進行調整時，應從整個電廠考慮，進行既安全又經濟的設計。

2.2 調整鍋爐廠的要求

鍋爐廠仍是向設計院提供兩組數據。一組是力的條件，必須滿足。一組是位移條件，角位移θx=θy=θz=0，必須滿足。自由熱膨脹線位移值不是限制條件，只作為設計院的參考。

2.3 不平衡廣義力分配法

鍋爐廠和設計院都根據已有的設計計算經驗，選擇適當的結構布置形式和構件幾何參數，把計算接口假定為固定邊界，進行各自系統的計算，雙方都得到各自在接口處的固端力系。這樣，在計算接口處就出現一組不平衡廣義力。把這組不平衡廣義力按相反方向分配給兩個計算系統。把分配后得到的這組計算接口處的內力作為各自的力的邊界條件，進行分析計算和結構上的調整。這種方法比較接近聯合計算。

不平衡廣義力的分配法有兩種。一種是按雙方系統的當量線剛度分配，一種是按雙方計算出來的固端廣義力大小分配。系統當量線剛度計算比較困難，因此本文選擇后者。以下以拉壓構件為例推導分配后的內力計算公式。

設鍋爐廠算出的固端力為P2，設計院算出的固端力為 P1，假定 P2>P1，不平衡力為 P2-P1。

按設計院側推導，需加上所分配的不平衡力

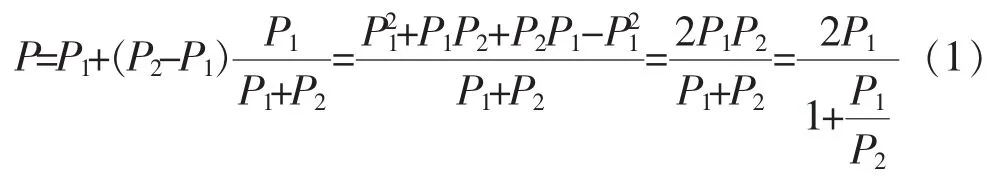
按鍋爐廠側推導，需減去所分配的不平衡力

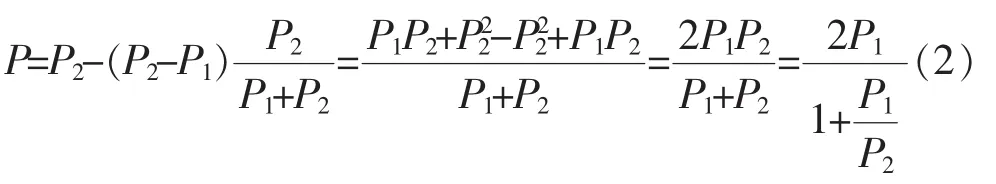
兩個結果完全相同。于是得到，分配后在計算接口處的內力為

應當指出，不平衡廣義力按固端力的大小進行分配所得到的計算內力不是精確解，因為它只滿足力的平衡條件，但不一定滿足變形協調條件。

舉例驗證該方法的準確度。設圖1是由兩段不同截面桿組成的兩端固定的直桿。在溫度上升t℃時，其內力的精確解［3］為

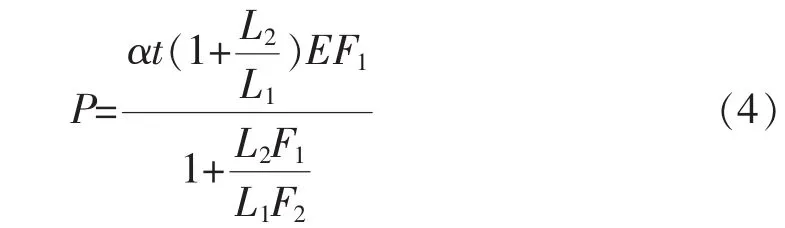
C點的不平衡力按AC和BC兩段桿件的線剛度進行分配可以得到與式（4）相同的精確解。如果按固端力進行分配，得到的內力為

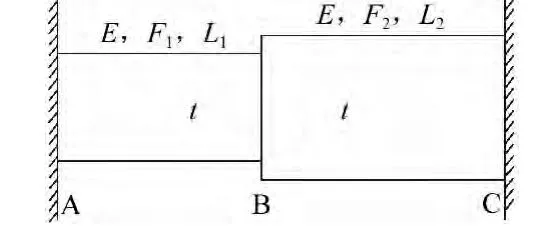
圖1 廣義不平衡力分配法示意圖

式（5）與長度 L1、L2沒關系，而若按線剛度進行分配，結果就與L1和L2有關。

比較式（5）和式（4），可以看出，當 L1=L2時，式（5）與精確解式（4）相同。

L1≠L2時，設 F2=2F1，按式（5）計算得＝1.333 33 αtEF1。對 L1>L2的情況，設 L1=1.5L2按式（4）算得 P=1.25 αtEF1，誤差<7%，式（5）偏大不到 7%。

L1

上述誤差在工程上是完全可以接受的。

3 結語

現行方法可以繼續使用，但如果把鍋爐自由熱膨脹量作為設計院計算的位移邊界條件，會得到較大的約束反力，則與力的限制條件相矛盾。

不平衡廣義力分配法，力學概念清楚，操作簡便，誤差不大，可以使用。此方法不但適用于亞臨界鍋爐，而且也適用于其他類型的鍋爐。

［1］ 中國動力工程學會.火力發電設備技術手冊第一卷鍋爐［M］.北京：機械工業出版社，2000.

［2］ 《中國電力百科全書》編輯委員會.中國電力百科全書火力發電卷［M］.北京：中國電力出版社，1995.

［3］ 杜慶華.材料力學（下冊）［M］.北京：高等教育出版社，1958.