風力機葉片三維氣動特性分析

李 碩

（大唐赤峰新能源有限公司，內蒙古 赤峰 024000）

0 引言

風能等可再生能源在能源工業中所占比重日益增加，大功率風力機葉片開發是目前風力機設計的一個重要問題。風力機葉片的主要功能是捕獲風的動能轉化為葉片的動能，風力機的效率主要取決于葉片的氣動外型設計。早期風力機葉片翼型主要取自于航空翼型，隨著風力機技術的發展，逐步開展了風力機專用翼型設計。通過風力機葉片的氣動特性分析，可以得到風力機風能利用系數及工作特性，同時可以得到風力機的氣動載荷，為風力機的結構設計提供依據。

目前風力機葉片氣動性能主要采用葉素動量理論（BEM），如文獻［1-3］。 隨著計算流體動力學（CFD）的發展及大型商業化CFD軟件的出現，給人們的數值模擬工作帶來了很大的便利，越來越多地人開始利用CFD軟件對風力機葉片的流場進行模擬，以便能夠設計出性能更好的風力機，如文獻［4-12］。目前對于風力機葉片的計算模擬，主要是對葉片翼型的二維流場進行分析［6-8，10］，得到葉片的某一截面的升力、阻力等設計參數。實際葉片是在三維旋轉流場的運動，葉片各截面弦長沿展長方向并不相同，并且葉片槳距角也隨著展長方向有一定變化，這樣二維流場計算出的結果會與實際情況有一定差異，尤其是對大型風力機葉片，采用二維流場計算誤差更大。

首先采用葉素動量理論（BEM）對NACA4412型葉片進行了氣動計算，然后采用FLUENT軟件對葉片進行三維流場分析，模擬實際風力機葉片工作情況，研究不同風速下的葉片的功率曲線圖，并與BEM理論計算結果相對比。

1 氣動特性計算方法

1.1 葉素動量理論

葉素動量理論假設作用于葉素上的力僅與通過葉素掃過圓環的氣體的動量變化有關。將葉片沿展長方向分成若干微段，每個微段稱為一個葉素。如圖1所示，當風以U∞并與弦線夾角為φ吹來，葉片的旋轉速度為Ω，旋轉半徑為r。考慮渦系的存在，流場中軸向速度和周向速度發生變化，引入軸向干擾因子a和切向干擾因子b，氣流相對于葉素的速度

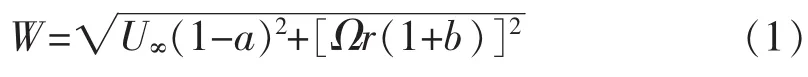
垂直于弦線方向的升力及沿弦線方向阻力

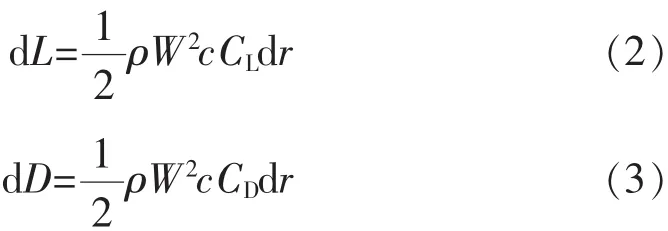
式中：ρ為空氣密度；c為弦長；CL為翼型的升力系數；CD為翼型的阻力系數。

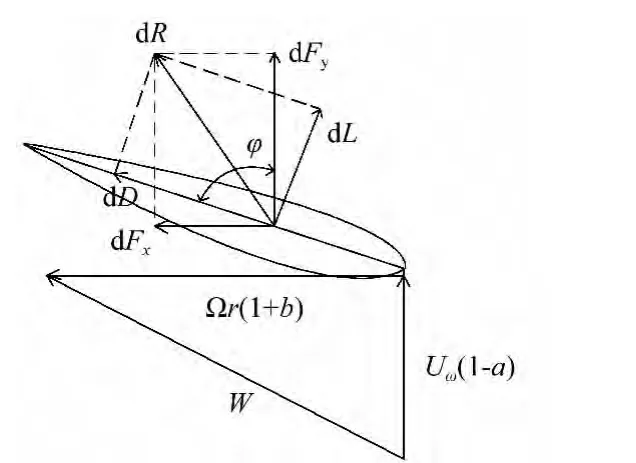
圖1 葉素受力及速度圖

則N個葉素上空氣動力分量在軸向上的推力如式（4），轉矩如式（5）。

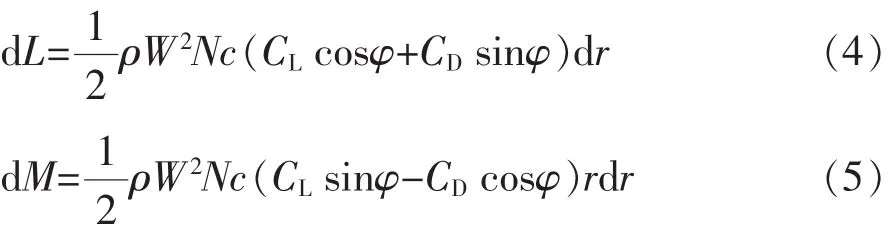
再由動量定理得出軸向推力如式（6），轉矩如式（7）。

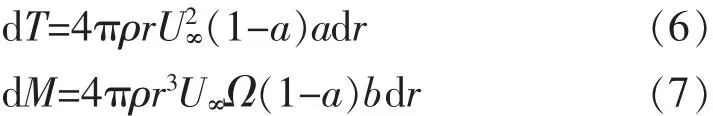
葉素動量理論結合了動量理論和葉素理論，式（4）與（6）相等，式（5）與（7）相等，因此可計算干擾因子a，b，并由式（7）可求得展長為dr的葉素產生的轉矩。

當考慮阻力的影響時

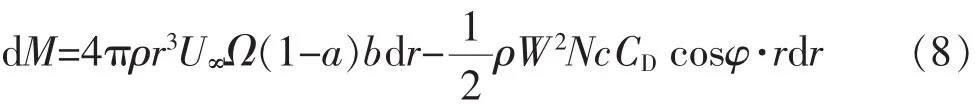
風力機葉片總功率為

1.2 CFD基本理論

流體運動的基本方程包括質量守恒、動量守恒和能量守恒方程，CFD采用數值計算方法來求解這些方程，得到流體運動特性。FLUENT求解器建立在有限容積法的基礎上，這種方法將計算域離散為有限數目的控制體或是單元。網格單元是FLUENT中的基本計算單位。在FLUENT中有兩種求解器，即分離求解器和耦合求解器。采用CFD方法計算流體運動主要步驟：1）通過網格劃分將空間區域分解成由離散的控制體組成的集合；2）在控制體上用積分形式構造離散變量的代數方程；3）將離散方程線性化，通過求解線性化方程獲得變量的迭代解。

2 葉片計算模型

某風力機葉片，設計參數如表1。

表1 葉片設計參數

在CATIA軟件中，根據葉片不同半徑處葉片翼型以及槳距角，取適當的點來畫出各個截面的翼型，并對截面翼型的樣條線進行光滑處理，最后放樣得出該葉片形狀，葉片的模型如圖2所示。

圖2 葉片三維模型

將模型導入GAMBIT軟件進行網格剖分和邊界條件設置。 由于場的范圍比較大，故使用T-grid型網格來對整個流體區域進行網格劃分。為了保證葉型部分的計算精度，將葉片表面網格細分，同時為了提高計算效率，外部的流場區域網格剖分的比較大。風力機葉片工作時都是旋轉的，為了更好的模擬葉片實際運行時的情況，將葉片周圍部分的空氣場與計算區域的外圍空氣場分開，并設定葉片周圍的流場是旋轉的，這樣可以模擬葉片的實際運行狀態。葉片計算場網格圖如圖3所示。

圖3 葉片計算場網格圖

將計算模型導入FLUENT進行計算。設置葉片的環境參數。湍流強度為5%，水力直徑為33.48 m，入口風速為15 m/s，空氣密度為1.225 kg/m3。風力機葉片在低馬赫數下工作，故在FLUENT中采用標準k-ε模型。 本文在計算時采用了一階迎風格式，為得到更加精確的結果也可采用二階迎風格式來提高計算精度。

3 計算結果

采用葉素動量理論計算得到葉片在不同風速下功率隨尖速比的變化曲線如圖4所示。

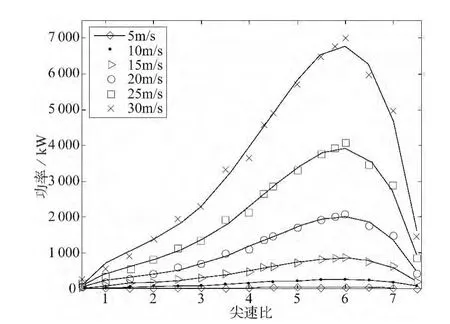
圖4 不同風速下尖速比—功率曲線圖（BEM）

采用CFD理論計算得到葉片在不同風速下功率隨尖速比的變化曲線如圖5所示。

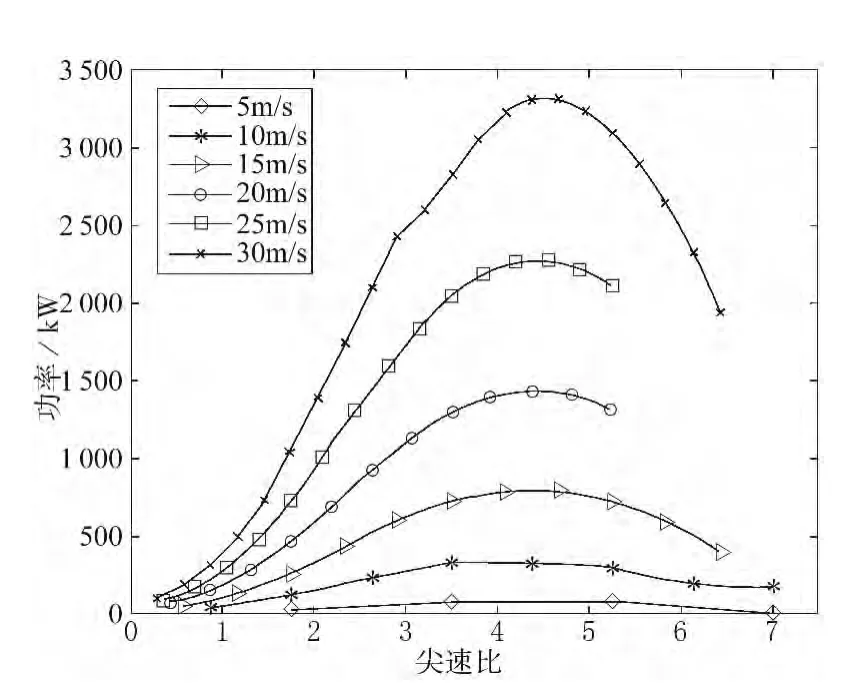
圖5 不同風速下尖速比—功率曲線圖（CFD）

從圖4、圖5中可以看出，隨風速的不同，葉片的額定轉速也不同，也就是風速越大時，將會產生更大的轉矩，在這種轉矩的作用下，葉片將會產生更大的旋轉速度。但在實際生產中葉片的額定轉速一般不大于20 rpm，葉片超過額定轉速后認為葉片失速。這樣，在風速比較大時其能量并沒有充分利用。從圖4中可以看出其功率曲線在尖速比6時取得最大值。從圖5中可看出，葉片功率在尖速比為4.7時取得最大值。從圖4和圖5中對比可以看出，按三維CFD方法計算得到的功率比BEM理論計算的功率要小，但兩種方法得到曲線形狀相似。差別的原因是由于在BEM理論中并沒有考慮流場的葉尖損失、葉根損失等因素的影響，而FLUENT計算時考慮了以上因素的影響，使得兩種分析結果存在一定差異。

葉片沿軸向的阻力如表2所示，葉片沿軸向的阻力隨著風速的增大而增大。但風阻系數為葉片的固有屬性，為定值，該葉片的阻力系數為0.188。 一般物體的阻力系數為0.15～0.4，本文計算結果合理。

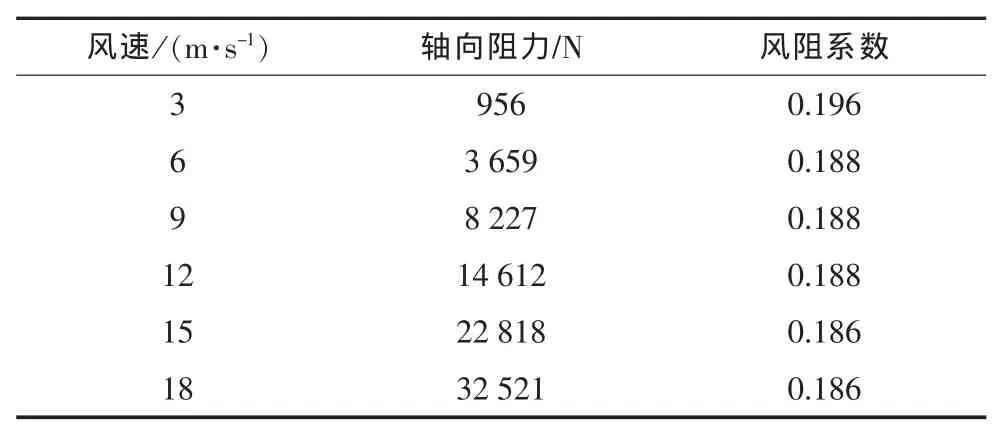
表2 不同風速下軸向風阻系數

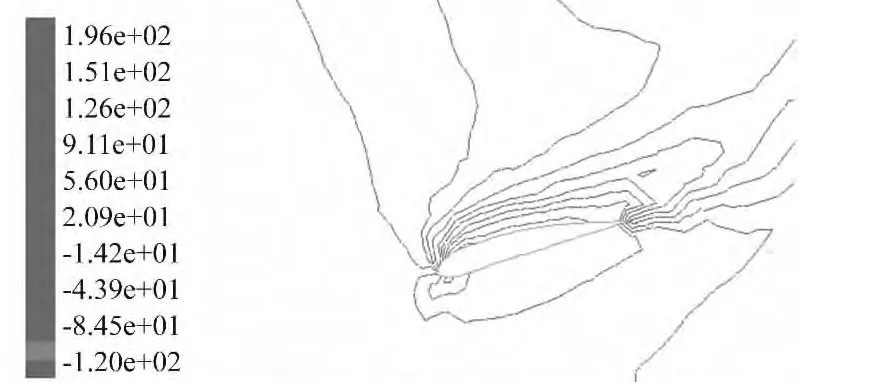
圖6 r/R=0.3截面處總壓強圖

圖6至圖9為葉片不同截面處的壓強圖，從圖中可以看出r/R=0.6時壓力梯度比r/R=0.3時大，說明葉片由于截面形狀、槳距角變化以及葉片的旋轉而產生不同的壓力場。圖10為葉片三維壓強分布圖，從圖中可以看出，葉片沿展長方向存在一定的壓差，而二維計算方法不考慮展長方向的空氣流動，導致產生誤差。故在大功率葉片流場分析時，為提高分析精度，應該采用三維CFD方法。

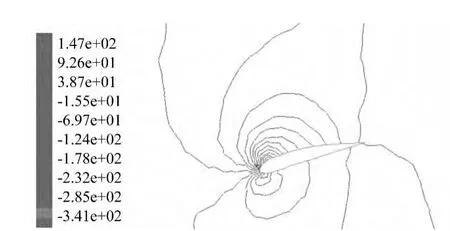
圖7 r/R=0.3截面處靜壓強圖

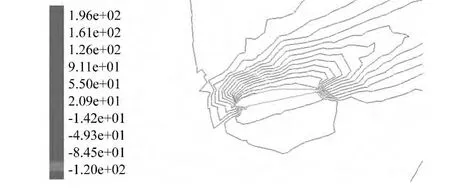
圖8 r/R=0.6截面處總壓強圖

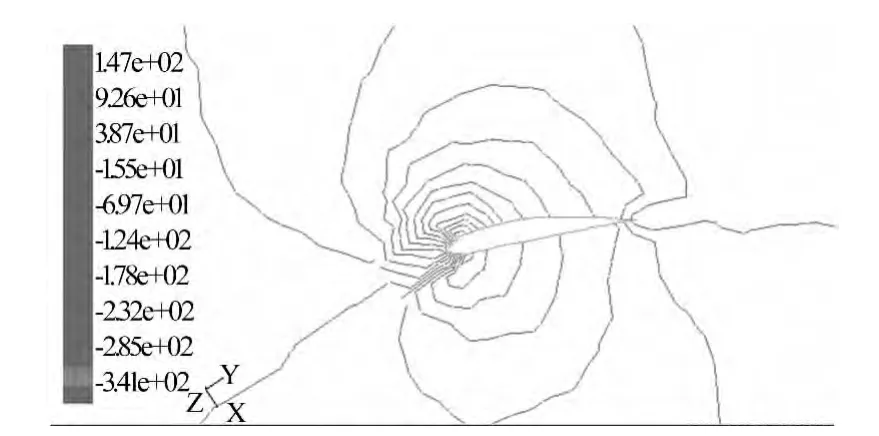
圖9 r/R=0.6截面處靜壓強圖

圖10 葉片三維總壓強圖

4 結語

采用BEM理論和三維CFD理論計算所得的風力機葉片功率曲線在風速較低時差異較小。當風速較大時，兩者結果存在較大的差別，三維CFD計算值明顯低于BEM理論計算值。

在大功率葉片氣動性能分析時，三維CFD理論可以模擬氣流壓力和流速沿葉展方向的變化，更接近葉片的實際工作情況。同時可到葉片各部位的載荷分布，為葉片的局部結構設計提供可靠的計算依據。

［1］ 張仲柱，王會社，趙曉路，等.水平軸風力機葉片氣動性能研究［J］.工程熱物理學報，2007，28（5）：781－783.

［2］ R.Lanzafame，M.Messina.Fluid dynamics wind turbine design：Critical analysis，optimization and application of BEM theory ［J］.Renewable Energy，2007，32：2 291－2 305.

［3］ 陳嚴，胡士山，葉枝全.定槳距風力機氣動優化設計優化方向分析［J］.太陽能學報，1997，18（3）：290－296.

［4］ 趙偉國，李仁年，李德順，等.風力機專用翼型數值模擬中湍流模型的選擇［J］，西華大學學報，2007，26（7）：61－62.

［5］ 胡丹梅，杜朝輝，朱春建.水平軸風力機靜態失速特性［J］.太陽能學報，2006，27（3）：217－222.

［6］ 陳旭，郝輝，田杰，杜朝輝.水平軸風力機翼型動態失速特性的數值研究［J］.太陽能學報，2003，24（6）：735－740.

［7］ 劉雄，陳嚴，葉枝全.增加風力機葉片翼型后緣厚度對氣動性能的影響［J］.太陽能學報，2006，27（5）：489－495.

［8］ 王海剛，戴韌.水平軸風力機動態來流條件下翼型氣動特性的數值分析［J］.工程熱物理學報，2007，28（3）：415－417.

［9］ 張玉良，李仁年，楊從新.水平軸風力機的設計與流場特性數值預測［J］.蘭州理工大學報，2007，33（2）：54－57.

［10］ 唐進.提高風力機葉型氣動性能的研究［D］.北京：清華大學，2004.

［11］吳春梅.風力機葉片的設計及其性能研究［D］.呼和浩特：內蒙古工業大學，2007.

［12］張智羽.帶小翼的風力機葉片氣動性能的數值模擬及其優化［D］.呼和浩特：內蒙古工業大學，2006.