永磁同步電機位置伺服系統滑模控制的研究

孫路路 王玲麗

(安徽工程大學 電氣工程學院，安徽 蕪湖241000)

0 引言

工業對象的多樣化和復雜化對伺服控制器提出了更高要求，即希望伺服系統具有一定的自適應能力和較強的抗擾能力，滑模變結構控制（SMC）能較好地解決這個問題[1]。SMC是50年代俄羅斯學者提出的一種有效的非線性魯棒控制方法[2]。由于它不需要對系統的精確觀測，控制率整定方法簡單，易于數字實現，近年來，已有學者將SMC應用于伺服系統中，研究表明，它能有效改善摩擦非線性和負載時變性，提高系統魯棒性[3-4]。

本文根據矢量控制PMSM伺服系統的特點，設計了一種SMC控制器，通過對控制量先微分后積分的處理，使其不含非線性項，減小了抖振；通過對伺服系統采取先速度SMC后位置SMC的方式，實現了位置跟蹤和速度控制。文中將該方法應用于矢量控制PMSM伺服系統，仿真和實驗結果均表明所設計的SMC控制器能使實際系統較好地實現位置跟蹤和速度控制，較大地提高系統的快速性和魯棒性，并減小抖振，有效地改善電機的動靜態特性。

1 永磁同步電機數學模型

假設磁路不飽和，在空間磁場呈正弦分布，不計磁滯和渦流損耗影響條件下，采用id=0的PMSM轉子磁場定向控制，轉矩的大小只與定子電流的幅值成正比，實現了PMSM的解耦控制。這時，PMSM電壓方程：

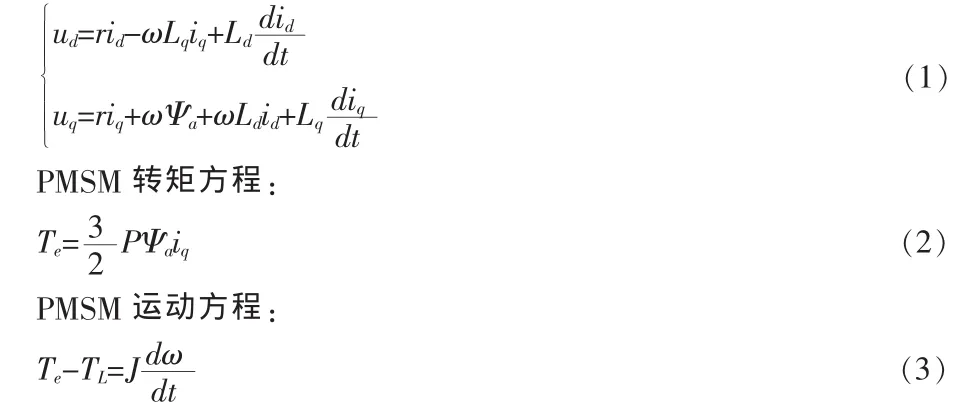
式中：ud、uq分別為 d、q 軸電壓；id、iq分別為 d、q 軸電流；Ld、Lq分別為 d、q軸電感；r為定子電阻；Te為電磁轉矩；P為電機的極對數；Ψa為永磁體與定子交鏈的磁鏈；TL為負載轉矩；J為轉動慣量；ω為轉子機械角速度。

2 控制器的設計

伺服系統采用圖1所示的控制方案，用SMC代替傳統P與PI的雙環控制。

SMC是基于相平面的控制，如圖2示。其基本思想是將任一點出發的狀態軌跡通過控制作用引導到滑模面（階段a），同時保證系統在滑模面上的運動是漸近穩定的，即為滑動模態（階段b）。

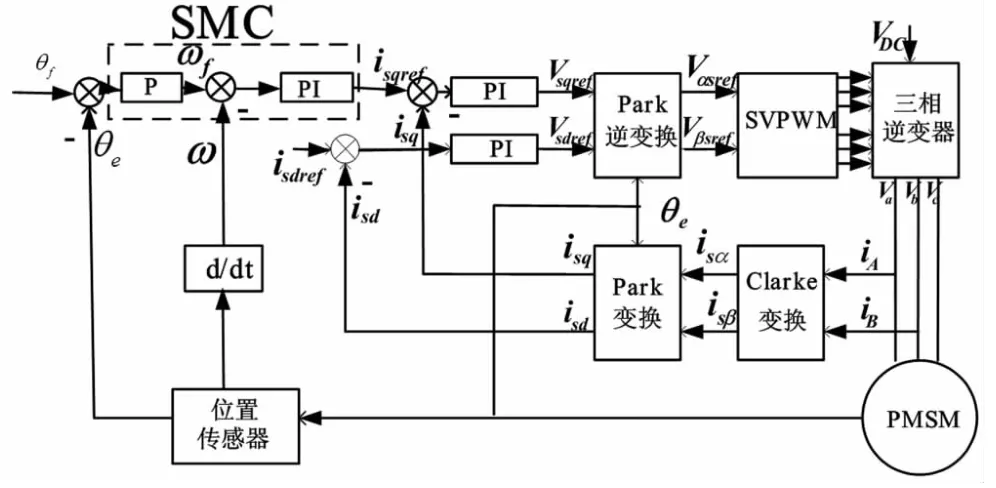
圖1 伺服系統框圖Fig.1 The structure of servo control system

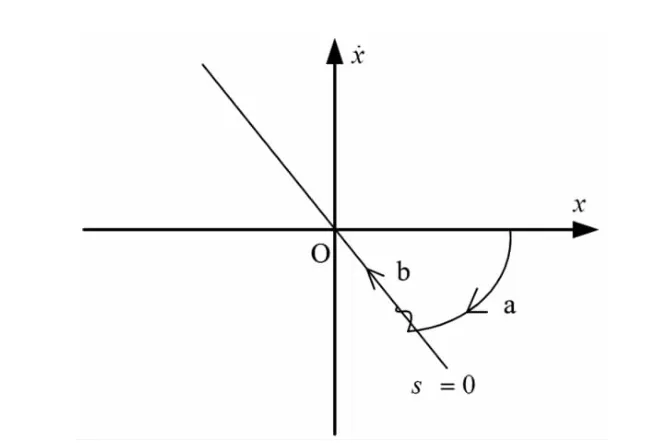
圖2 SMC系統相平面軌跡Fig.2 The phase trace of SMC system

對系統位置采取SMC控制，取系統狀態變量：

設計切換函數：

則由SMC到達條件 ss˙＜0得：

圖4是在給定角度200°時，采用位置SMC的仿真波形。可見，系統最終能無超調地達到穩定。

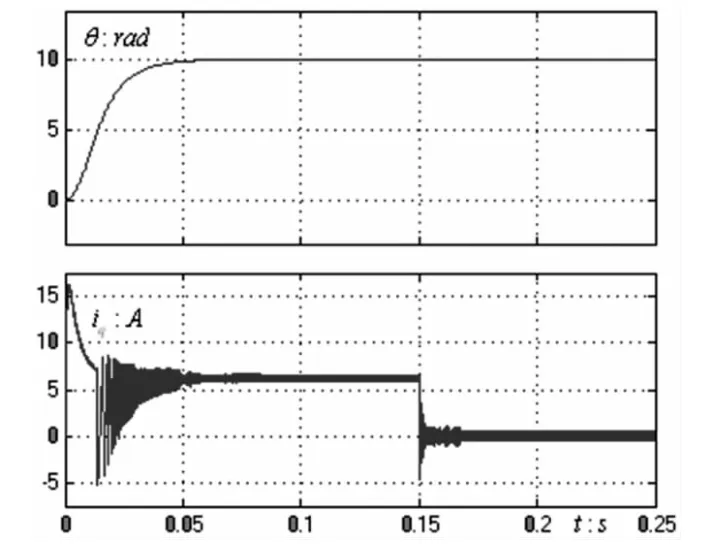
圖3 突卸負載iq和位置誤差波形

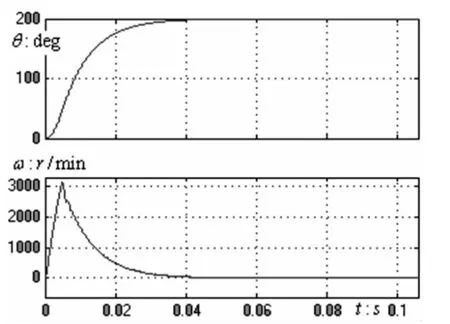
圖4 伺服系統位置和速度波形

3 結論

本文針對矢量控制的PMSM伺服系統的特點，設計了一種SMC控制器，仿真表明，所設計的SMC控制器能有效實現PMSM速度和位置伺服。

［1］Kuo-Kai Shyu，Chiu-Keng Lai，Yao-Wen Tsai,，and Ding-I Yang.A Newly Robust Controller Design for the Position Control of Permanent-Magnet Synchronous Motor[J].IEEE Transaction on Industrial Electronics，2002，49（3）：558-565.

［2］葛寶明，鄭瓊林，蔣靜坪，于學海.基于離散時間趨近率控制與內模控制的永磁同步電動機傳動系統[J].中國電機工程學報，2004，24（11）：106-111.

［3］張希，陳宗祥，潘俊民，王杰.永磁直線同步電機的固定邊界層滑模控制[J].中國電機工程學報，2006，26（22）：115-121.

［4］劉云峰，繆棟.電液伺服系統的自適應模糊滑模控制研究[J].中國電機工程學報，2006，26（14）：140-144.