雙目視覺系統精度分析及在經絡可視化中的應用

林雪華，陳新

福州大學 物理與信息工程學院，福建 福州 350108

雙目視覺系統精度分析及在經絡可視化中的應用

林雪華，陳新

福州大學 物理與信息工程學院，福建 福州 350108

為提高雙目立體視覺測量系統的測量精度，采用三角法建立雙目立體視覺測量系統的結構參數模型，分析系統結構參數對測量結果的影響。通過仿真得出各結構參數對測量結果的精度影響趨勢，歸納出小誤差的結構參數取值范圍，并將分析結果應用于經絡可視化研究中。通過在電極探針上粘貼定位標靶，利用標靶與電極探針的關系計算出探針的坐標，從而間接得出經絡點的位置。通過對標靶中X角點的定位精度進行分析，得出實驗操作的有效工作區域，為經絡的準確定位奠定了良好的基礎。最后，根據理論與實驗結果總結出提高系統精度的方法。

超聲儀；經絡可視化；角點檢測；雙目立體視覺；結構參數；誤差分析

0 前言

中醫認為，經絡調控人體氣血的運行，是人體臟腑聯絡體表及全身各部的通道[1]。對經絡、穴位的準確定位，特別是在人體體表上實時顯示，對于臨床診斷、治療和療效的評估具有重要的意義和臨床應用價值。目前常用的經絡定位方法有超聲定位、紅外定位、磁定位和光學定位，其中光學定位與其他方法比較具有測量誤差小、受環境影響小和無傷害等優點。

本文結合經絡的低阻抗電學特性[2]，利用雙目立體視覺系統，研究一種經絡的實時定位和顯示的新方法，在人體體表上直接測量并實時繪制經絡的準確位置。其實現思想為：在探針表面粘貼定位標靶，利用雙目立體視覺系統對標靶進行定位，之后根據標靶與探針的相對位置關系，計算出探針的位置。當探針與人體體表皮膚所接觸位置的電特性符合低阻抗特性時，探針所在的位置即為經絡候選點。經絡的準確定位依賴于雙目立體視覺系統對標靶的準確定位，因而雙目立體視覺系統的精度對經絡點的定位準確性至關重要。

1 雙目立體視覺系統的有效視場

雙目立體視覺是計算機視覺的一個重要分支，原理是從兩個或更多的視點觀察同一景物，從而獲取不同視角下的感知圖像，通過三角測量原理計算圖像視差來獲取被測目標的三維信息[3]。

雙目立體視覺系統如同人的眼睛，具有一定的可視范圍，即稱為有效視場。假設兩攝像機具有相同的參數，且對稱放置，見圖1，其中o1、o2分別表示兩攝像機的光心，z1、z2表示光軸，光心的連線為基線距B，攝像機的視場角為2ω，光軸與Z軸的夾角為φ，w為視場寬度。空間中任意目標點到基線的距離為d，可得雙目視覺系統的有效視場滿足關系：

圖1 雙目立體視覺可視區域

2 雙目立體視覺測量系統結構參數模型

雙目立體視覺測量系統模仿人眼的功能，基于視差原理，利用空間點在攝像機像面上的成像點坐標求取空間點的三維坐標。一個完整的雙目立體視覺測量過程通常分為圖像獲取、攝像機標定、特征提取、立體匹配、三維重建等5個步驟。在實際測量過程中，一旦系統標定后，系統中的攝像機的焦距，攝像機之間的夾角和相對位置等都必須保持固定不變，因此測量工作開始之前有必要對系統結構進行優化[4]。

雙目立體視覺測量系統在XO1Z平面的投影圖，見圖2。圖中兩臺攝像機為水平交向放置，O1，O2為其透鏡中心，有效焦距為f1，f2，兩透鏡中心的連線稱為基線距B，兩攝像機光軸與基線的夾角分別為α1，α2。O1P1，O2P2分別為兩攝像機的成像平面，其中P1，P2分別為空間點P在兩攝像機成像平面上的像點。ω1，ω2為P點在水平面上與光軸的夾角，即為水平視場角。由圖2可知，直線O1P1和直線O2P2相交于點P，因此點P是唯一的，其三維空間位置是可確定的。

圖2 雙目立體視覺測量系統結構模型

根據圖2的幾何關系，以左攝像機C1XYZ為世界坐標，可以利用系統結構參數和視場角來表示空間點P的三維坐標為：

3 雙目立體測量系統的精度分析及仿真

雙目立體視覺測量系統的結構參數主要有兩攝像機光軸與基線之間的夾角α1、α2，基線距B、工作距離Z，焦距f等，這些結構參數存在的約束關系[5]。為得到準確的測量結果，首先需要對相關結構參數進行誤差分析和處理。

假設目標點P處于圖1的有效視場中，根據誤差理論分析[6]，用X、Y和Z方向的測量誤差表示坐標測量綜合誤差：

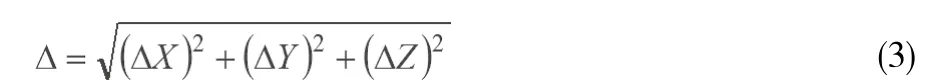
其中：

式中δi為像點坐標值提取誤差，i表示像點x1，x2，y1，y2。

為了提高雙目立體視覺系統的定位精度，對以下各結構參數進行分析并仿真。

3.1 光軸與基線夾角和視場角對測量精度的影響

對于一個既定的系統，其結構參數是固定不變的，且這些結構參數也經過精心標定，其標定誤差也是定值，綜合測量誤差只是隨著目標點視場的變化而變化。視場角分為水平視場角和垂直視場角，系統綜合誤差隨著垂直投影角的增大而單調增大。假設像點坐標提取誤差為δx=δy=δ，水平視場角ω1∈[-40°，40°]，ω2∈[-40°，40°]， 光軸與基線的夾角α1=α2=40°，根據式(3)可得到誤差的分布，見圖3。

圖3 水平視場角與誤差分布

由圖3可知，兩水平視場角在[-20°,20°]范圍時，綜合測量誤差相對較小。當 ω1=ω2=ω∈[-25°,25°]時，誤差傳遞函數將隨著光軸與基線的夾角α1=α2=α取值不同而發生變化，為了視圖清晰只畫出部分曲線，見圖4。從圖4可以看出，當α取值在[40°,50°]時，系統綜合誤差較小且均勻分布。

圖4 光軸與基線夾角與誤差分布

3.2 焦距f對測量精度的影響

焦距f是透鏡的主要參數之一。焦距不同的攝像機，視場范圍也不同，光路越長，視場范圍越小。為了分析不同的焦距對測量精度的影響，假設光軸與基線的夾角α=40°，ω∈[-40°,40°]，改變f的值，誤差分布，見圖5。

圖5 焦距對系統誤差的影響

從圖5可以看出，隨著焦距f增大，系統誤差減小，且誤差分布較短焦距均勻，因此在實際測量中，可以通過適當增大焦距提高系統精度。

3.3 基線距B對測量精度的影響

雙目立體視覺測量系統中兩攝像機之間的透鏡中心距離為基線距。當其增大時，相應的測量角 將隨著增大，使得B對精度的影響呈非線性。有文獻[7]指出位于攝像機光軸上的點測量精度最低。因此，可通過研究兩攝像機光軸的交點位置P的誤差來分析基線距B對系統誤差的影響。

設α1=α2=α，ω1=ω2=0，k=B/Z為基線距與工作距離的比值，f為攝像機的有效焦距，得空間點P的坐標傳遞函數為：

P點的綜合測量誤差為：

當系統固定后，Z和f為定值，則綜合測量誤 差與 成正比。根據式（6），可得測量誤差與基線距的關系，見圖6。

圖6 測量誤差隨結構參數的變化關系圖

由圖6可知，綜合測量誤差隨著k的增大，先減小后增大；當k在0.8～1.8之間變化時，系統的綜合測量誤差較小,并在k=1.3附近有最小值；當k＜0.5或k＞2.5時，k的變化對測量精度影響較大。

4 經絡可視化中定位精度的提高

經絡的可視化依賴于雙目立體系統對經絡點進行定位。本文中采用的方法是在探針上粘貼定位標靶，見圖7。通過對標靶上的X角點進行定位，之后根據X角點與電極探針的固有相對位置關系，從而計算出探針的坐標。圖7中P0、P1、P2為3個X角點，Ci為第i個電極探針觸點，圖中探針觸點具有以下特征：① 探針觸點連線C1C16與直線P0P2平行；② 探針等距離d分布；③ 最右邊的探針C1在直線P0P1上。

根據C1點在直線P0P1上以及C1點與P0的距離D1、P0與P1的距離D2三個約束條件，結合標靶中角點的三維坐標，可求得第一通道的探針觸點C1的三維坐標(x1, y1, z1)。

根據上述特征①，可以求得直線C1C16的方程，并根據第i通道Ci與C1的距離分布，插值求出Ci(xi, yi, zi)，其中1＜i＜17。

計算出各探針觸點的三維坐標后，結合阻抗檢測儀對探針所接觸的皮膚阻抗的檢測數據，根據經絡的低阻抗特性可知經絡點所處的探針通道，即可得出經絡點所處的三維坐標。

圖7 標靶及探針關系

根據以上思想，要實現經絡的精確定位，需確保X角點三維定位的精度。以左攝像機坐標系為世界坐標系，假設三維重建得到的X角點三維坐標是準確的，則反投影到左攝像機成像平面上的X角點二維坐標應該與左攝像機自身檢測到的X角點二維坐標相同。根據此原理及結構參數對系統誤差影響的仿真結果設計實驗如下。

主要儀器：德國The ImagingSource生產的DMK 41AUC02 USB CMOS單色相機2臺（分辨率為1280×1024，像元尺寸為5.2μm×5.2 μm）。瑞士Leica激光測距儀D21臺（測程0.05 m～60 m，精度 1.5 mm）。

實驗步驟：

（1）先采用張氏標定法[8]對左右攝像機標定，得到左右攝像機的內外參數。根據前文仿真結果可知，當光軸與基線的夾角在[40°,50°]、兩水平視場角在[-20°,20°]范圍內時，綜合測量誤差相對較小。因此調整攝像機使α1=α2=50°，水平視場角ω=5°，左右攝像機對稱放置，左右攝像機基線距B=900 mm，焦距f=12 mm。

（2）采用Harris[9]檢測算法對圖7所示標靶上的3個X角點進行檢測，并進一步對亞像素級提取，得到亞像素級二維坐標。

（3）實現左攝像機所檢測的X角點與右攝像機檢測到的X角點的立體匹配，以左攝像機為世界坐標，根據雙目立體視覺原理進行X角點三維坐標重建。

（4）把所得到的三維坐標反投影到左攝像機成像平面上，通過計算反投影后二維坐標與左攝像機自身檢測到的二維坐標偏離距離來衡量系統的誤差。假設左攝像機檢測到的X角點坐標為（xi，yi），反投影到左攝像機成像平面上得到的坐標X角點為 ，3個X角點的平均誤差公式定義為。

（5）在有效視場范圍內改變標靶與攝像機的距離，重復步驟（2）～（4）。

根據以上實驗步驟，得到實驗結果，見表1。

從實驗結果可知，當工作距離在0.7 m左右，基線距為0.9 m時，即基線距與工作距離的比值為1.3左右反投影后所得的坐標與左攝像機自身檢測的角點坐標偏差在0.5 pix左右，精度較高。從公式(4)～(6)可知，對于既定的系統，綜合誤差與e成正比，在k=1.3附近具有最小值（圖6）。實驗結果與理論分析吻合。在基線不改變的情況下，增大或減小工作距離，X角點的定位精度都將降低，在工作距離1 m時誤差最高將達到7 pix左右。

為了驗證經絡點檢測具有可行性，假設工作距離為0.7 m，工作平臺為1 m2，沿著與基線平行的方向移動電極探針，重復檢測角點并計算誤差。實驗結果顯示，角點的定位誤差在工作臺的中心區域在0.5 pix左右，以視場中心點為圓心，半徑為0.3～0.4 m的圓內精度相對穩定，邊緣區域誤差將達到3～4 pix，即視場中心的X方向和Y方向測量精度高于邊緣的測量精度[10]。因此，只要確保實驗操作在以上有效區域內，可以得到精度較高的經絡點。

實驗中以部分心包經為例，首先計算出角點的三維坐標，結合經絡點的低阻抗特性，利用圖像融合算法將經絡點顯示在二維場景圖像中。心包經的檢測結果，見圖8中左圖。然后利用曲線擬合的方法連接經絡點，見圖8中右圖。

圖8 經絡可視化

從以上分析及實驗結果可知，誤差傳遞系數是非線性的，從兩方面影響系統的綜合誤差：一方面是系統結構參數(B, α1，α2、 ω1，ω2、f1、f2)和標定值的誤差；另一方面是兩攝像機圖像平面上像點的坐標值（X1、X2、Y1、Y2）及其提取誤差δ[11-12]。

表1 實驗結果

結合仿真與實驗，可從以下幾個方面對系統進行優化：

（1）合理選擇攝像機內部參數及鏡頭焦距，盡可能選高分辨率的攝像機。在角點定位實驗中，工作距離較小，結合精度和視場要求選擇焦距為12 mm攝像機。攝像機的有效焦距越大，系統的精度越高，但是視場范圍越小。所以必須根據測量對象和測量環境選擇合適的攝像機。

（2）根據被測物體的特點系統的體積等因素初步確定測量的工作距離和基線距。實驗中當工作距離為0.7 m左右，基線距為0.9 m時精度較高。如果需要工作距離較大的系統，要求基線距B也必須增大，當兩者的比例為1.3時，才能達到比較高的精度。在系統結構已經確定時，工作距離越大,精度則越低。

（3）結合公式(1)，根據實驗中對有效視場大小的需求，調整攝像機間的夾角。當光軸與基線的夾角為[40°，50°]可得到較小的誤差。

（4）被測物體的放置與光軸在同一水平面，即垂直視場角為零，水平視場角在[-20°,20°]范圍內為最佳。

（5）Harris 角點檢測算法得到的是像素級的坐標，為了提高精度，需進一步亞像素提取。所以為了減小坐標提取誤差，必須選擇合理軟件算法。

5 結束語

本文通過對雙目立體視覺系統的可視區域范圍和結構參數進行分析，并結合仿真得知結構參數的最佳取值范圍，之后設計實驗對經絡可視化中定位標靶中X角點的三維重建精度進行分析。本文提出的方法為提高經絡定位的精度奠定了良好工作基礎，通過優化系統結構參數及軟件算法的合理選擇，可以得到高精度的X角點坐標。

[1] 黃輝．經絡[J]．中醫藥臨床雜志,2012,24(10):1001．

[2] 祝總驤,徐瑞民,謝君國,等．經絡在表皮層和角質層的低阻抗特性及其形態學實質的研究[J]．中國醫藥學報,1988,3(5):33-35．

[3] 吳彰良,孫長庫,楊中東．視覺測量傳感器系統結構參數設計分析[J]．光電工程,2009, 36(12):56-61．

[4] 閆龍,趙正旭,周以齊．基于CCD的立體視覺測量系統精度分析與結構設計研究[J]．儀器儀表學報,2008,29 (2):410-413．[5] 劉亞菲,郭慧,聶冬金,等．雙目立體視覺系統測量精度的分析[J]．東華大學學報,2012,5(38):572-576．

[6] 費業泰．誤差理論與數據處理[M]．北京:機械工業出版社,2004: 58-59．

[7] 張廣軍．機器視覺[M]．北京:科學出版社,2005:102-104．

[8] Zhengyou Zhang．A flexible new technique for camera calibration[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000,22(11):1330-1334．

[9] 姚耀,胡仲翔,時小軍,等．Harris 角點提取實現亞像素級攝像機自標定[J]．電子設計工程,2009,17(5):61-65．

[10] 李海濱,單文軍,劉彬．雙目立體視覺測距系統誤差模型的研究[J]．光學技術,2006,32(1):24-30．

[11] 趙萍,李永奎,田素博,等．雙目視覺測量系統結構參數理論與試驗研究[J]．機械設計,2013,30(2):64-68 ．

[12] Yubo Guo,Yu Yao,Xiaoguang DI．Research on structural parameter optimization of binocular vision measuring system for parallel mechanism[J]．IEEE International Conference on Mechatronics and Automation,2006,25(28):1131-1135．

Accuracy Analysis of Binocular Vision System and Its Application in Meridian Visualization

LIN Xue-hua, Chen Xin
College of Physics and Information Engineering, Fuzhou University, Fuzhou Fujian 350108, China

In order to improve the measurement precision of binocular stereo vision measuring system, a new structural parameter model of this system was investigated with the trigonometric method to analyze the structural parameters affect on the vision measurement accuracy. Then, by simulation, the precision infuence trend of these structural parameters was got to conclude the range of the structural parameters with a small error. And, the simulation result could be applied to the meridian visualization. By pasting the location target on the electrode probe, the coordinates of the probes was calculated by using the relationship of target and electrode probes to indirectly get meridian point position. Also, by analyzing the accuracy of the X corners on the target, this experiment obtained an effective work area which laid a good foundation for the meridian visualization. Finally, according to the theoretical and experimental results, the method of improving system precision was summarized.

ultrasonic apparatus; meridian visualization; corner detection; binocular stereo vision; structural parameter; error analysis

TP391.41

A

10.3969/j.issn.1674-1633.2014.03.005

1674-1633(2014)03-0016-05

2013-09-23

福建省自然科學基金項目（2012J01267）。

本文作者：林雪華，碩士研究生。

陳新，教授，主要研究生物醫學，圖像處理與網絡通信。

作者郵箱：meltingsnow@139.com