定積分計算的新公式及其應用

符云錦

（鳳凰縣兩林學區，湖南鳳凰416211）

定積分計算的新公式及其應用

符云錦

（鳳凰縣兩林學區，湖南鳳凰416211）

利用含參變量的拉普拉斯變換，推導出不同于牛頓-萊布尼茨公式的計算定積分的1個新公式，并舉例說明該公式使用方法。

含參變量的拉普拉斯變換；定積分；新公式

0 引言

文獻[1]給出了如下含參變量的拉普拉斯變換的定義：

文獻[1]中還給出了含參變量的拉普拉斯變換的存在性和基本性質；還利用含參變量的拉普拉斯變換，推導出了一些常用的含參變量的拉普拉斯變換的公式。

本文利用含參變量的拉普拉斯變換，推導出計算定積分的1個新公式，并舉例說明如何用該公式來計算定積分。

1 計算定積分的新公式

定理1設函數f(t)在內有定義，并且可積，則有

證根據定積分性質，有

形式上有些相似，但本質上完全不同。一個是被積函數的象函數的函數值之差，另一個是被積函數的原函數的函數值之差。因此，式（2）是計算定積分的一個全新的公式。下面舉例說明其在定積分計算中的應用。

2 實例計算

由含參變量的拉普拉斯變換的齊次性質和位移性質得

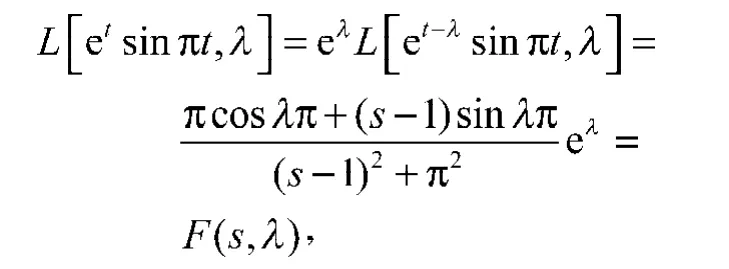
由含參變量的拉普拉斯變換的齊次性質和位移性質得

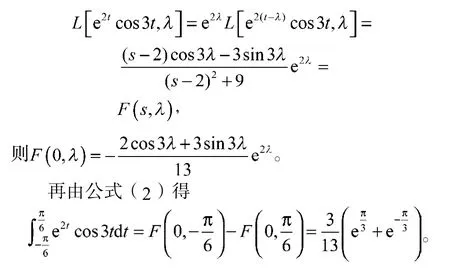
3 結語

[1]陽凌云，符云錦，鄧光輝. 含參變量的拉普拉斯變換及其應用[J]. 湖南工業大學學報，2012，26(1)：1-5. Yang Lingyun，Fu Yunjin，Deng Guanghui. The Laplace Transform with Parameters and Its Application[J]. Journal of Hunan University of Technology，2012，26(1)：1-5.

[2]焦存德. 牛頓-萊布尼茨公式條件的研究[J]. 濟南職業學院學報，2014(1)：57-58.

Jiao Cunde. The Study on the Conditions of Newton-Leibniz Formula[J]. Journal of Jinan Vocational College，2014(1)：57-58.

[3]賽鬧爾再. 試論牛頓-萊布尼茨公式[J]. 才智，2013 (32)：34. Sai Naoerzai. On Newton-Leibniz Formula[J]. Intelligence，2013(32)：34.

[4]李愛琴. 牛頓-萊布尼茲公式的“引導發現式”教學[J].佳木斯教育學院學報，2013(12)：145-146. Li Aiqin. Newton-Leibniz Formula "Guided Discovery" Teaching[J]. Journal of Jiamusi Education Institute， 2013 (12)：145-146.

[5]張豫岡，王新愛. 牛頓-萊布尼茨公式的一種證明方法[J]. 吉林省教育學院學報，2013，29(5)：153-154. Zhang Yugang，Wang Xinai. A Way to Prove Newton-Leibniz Formula[J]. Journal of Educational Institute of Jilin Province，2013，29(5)：153-154.

[6]張豫岡，王新愛. 牛頓-萊布尼茨公式的證明與幾何解釋[J]. 蘭州工業學院學報，2013，20(2)：65-68. Zhang Yugang，Wang Xinai. Proof and Geometric Interpretation of Newton-Leibniz Formula[J]. Journal of Lanzhou Institute of Technology，2013，20(2)：65-68.

（責任編輯：鄧光輝）

A New Formula for Definite Integral Calculation and Its Application

Fu Yunjin
（Lianglin School District，Fenghuang Hunan 416211，China）

By using Laplace transform with parameters, derives a new formula for definite integral calculation which differs from Newton-Leibniz formula, and illustrates the formula method of use.

Laplace transform with parameters；definite integral；new formula

O172.2

A

1673-9833(2014)04-0012-02

10.3969/j.issn.1673-9833.2014.04.003

2014-03-17

符云錦（1984-），男，湖南瀘溪人，湖南鳳凰縣兩林學區教師，主要研究方向為初等數學，分析學及其應用，微分方程，教育理論及其應用，E-mail：wsasw4264731123@163.com