縮短多級風(fēng)扇/壓氣機(jī)三維計算周期的方法

蔡留成，王 俊，劉蕊蕊

(中國燃?xì)鉁u輪研究院，四川 成都 610500)

1 引言

隨著軍用發(fā)動機(jī)對風(fēng)扇/壓氣機(jī)部件的要求越來越高，級負(fù)荷逐漸提高，風(fēng)扇/壓氣機(jī)內(nèi)部氣流三維流動效應(yīng)明顯。目前，大部分研究機(jī)構(gòu)采用三維軟件進(jìn)行流場分析。三維軟件能較全面地反映風(fēng)扇/壓氣機(jī)的流場特征，但受目前計算機(jī)運(yùn)行速度的限制，加之風(fēng)扇/壓氣機(jī)級數(shù)多，若再考慮結(jié)構(gòu)細(xì)節(jié)，網(wǎng)格數(shù)量將非常龐大，設(shè)計效率較低。為解決該問題，國內(nèi)外研究機(jī)構(gòu)通過提升計算機(jī)軟硬件水平來提高計算能力，但目前計算機(jī)的運(yùn)算能力已近極致，提升空間非常有限。若將多級風(fēng)扇/壓氣機(jī)設(shè)計分解為多個單級風(fēng)扇/壓氣機(jī)設(shè)計，網(wǎng)格數(shù)量將大幅降低，而且還可進(jìn)行多人多平臺設(shè)計，從而節(jié)省大量時間，但涉及級間匹配問題[1]。工程上較多使用級疊加法進(jìn)行壓氣機(jī)級間匹配，其理論依據(jù)是假定在下游疊加上去的葉片排不影響上游原有流場[2]。對級疊加法國內(nèi)外已有較多研究，從上世紀(jì)五六十年代至今，國外 Robbins[3]、Klapprot[4]、Soltani[5]等及國內(nèi)曲愛民[6]等對級疊加法進(jìn)行了研究。

本文以疊加理論為基礎(chǔ)，對某三級風(fēng)扇進(jìn)行適當(dāng)拆分，然后分別進(jìn)行全三維計算。對比分析計算結(jié)果與聯(lián)算結(jié)果，發(fā)現(xiàn)采用該方法計算的各級氣動流場與三級聯(lián)算流場基本一致。為驗證該計算方法的有效性，選取一型高壓壓氣機(jī)的第三、四級進(jìn)行了計算驗證。

2 計算方法

本文計算采用NUMECA軟件，紊流模型采用SST模型，計算格式選用中心差分格式，對三級風(fēng)扇第一級(包括IGV)、前兩級(包括IGV)及后兩級進(jìn)行三維計算。計算時所有葉排均采用AUTOGRID5的默認(rèn)網(wǎng)格，機(jī)匣與轉(zhuǎn)子葉片的間隙全部取0.2 mm，網(wǎng)格細(xì)節(jié)見圖1。

3 計算結(jié)果分析

3.1 風(fēng)扇計算結(jié)果分析

以設(shè)計點(100%相對換算轉(zhuǎn)速)為計算工況，對風(fēng)扇設(shè)計點下第一級、前兩級、后兩級及整個風(fēng)扇進(jìn)行了NUMECA全三維數(shù)值計算，計算所采用的邊界條件均來自風(fēng)扇設(shè)計工況下結(jié)果。計算完后作如下選取：取單算的第一級計算結(jié)果為第一級參數(shù)，取前兩級聯(lián)算的后面級計算結(jié)果為第二級參數(shù)，取后兩級聯(lián)算的后面級計算結(jié)果為第三級參數(shù)。采用該方式計算得到的性能參數(shù)對比見表1。可見，第一級單算、前兩級聯(lián)算的流量與三級聯(lián)算的流量基本一致，后兩級聯(lián)算時的流量略微偏大。這說明在設(shè)計轉(zhuǎn)速時，整個風(fēng)扇流量主要是受到第一級的控制，風(fēng)扇后面級流量逐級增大，符合風(fēng)扇/壓氣機(jī)設(shè)計規(guī)律。從各級壓比和效率對比也可看出，采用這種方式得到的各級壓比和效率，與三級聯(lián)算的各級壓比和效率基本相同。

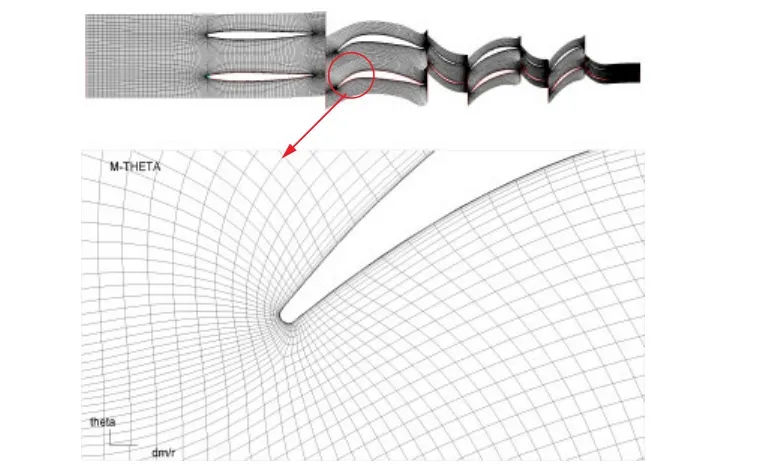
圖1 網(wǎng)格細(xì)節(jié)示意圖Fig.1 Detailed grid map

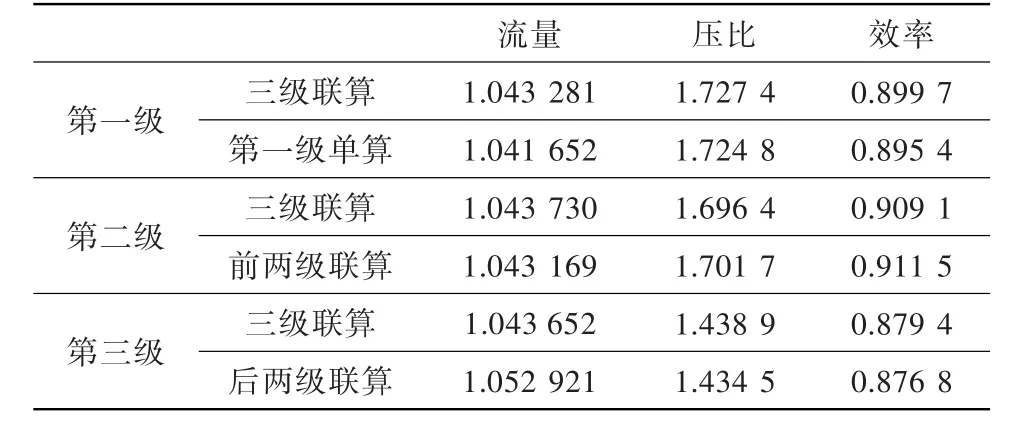
表1 各計算方式的三維計算結(jié)果Table 1 The results of the all computed modes

以設(shè)計轉(zhuǎn)速下的計算結(jié)果為例，對采用本文計算方式下的各級流場參數(shù)與整個風(fēng)扇部件聯(lián)算結(jié)果進(jìn)行對比分析。圖2～圖4分別為5%、50%和95%葉高擬S1流面馬赫數(shù)等值線圖。

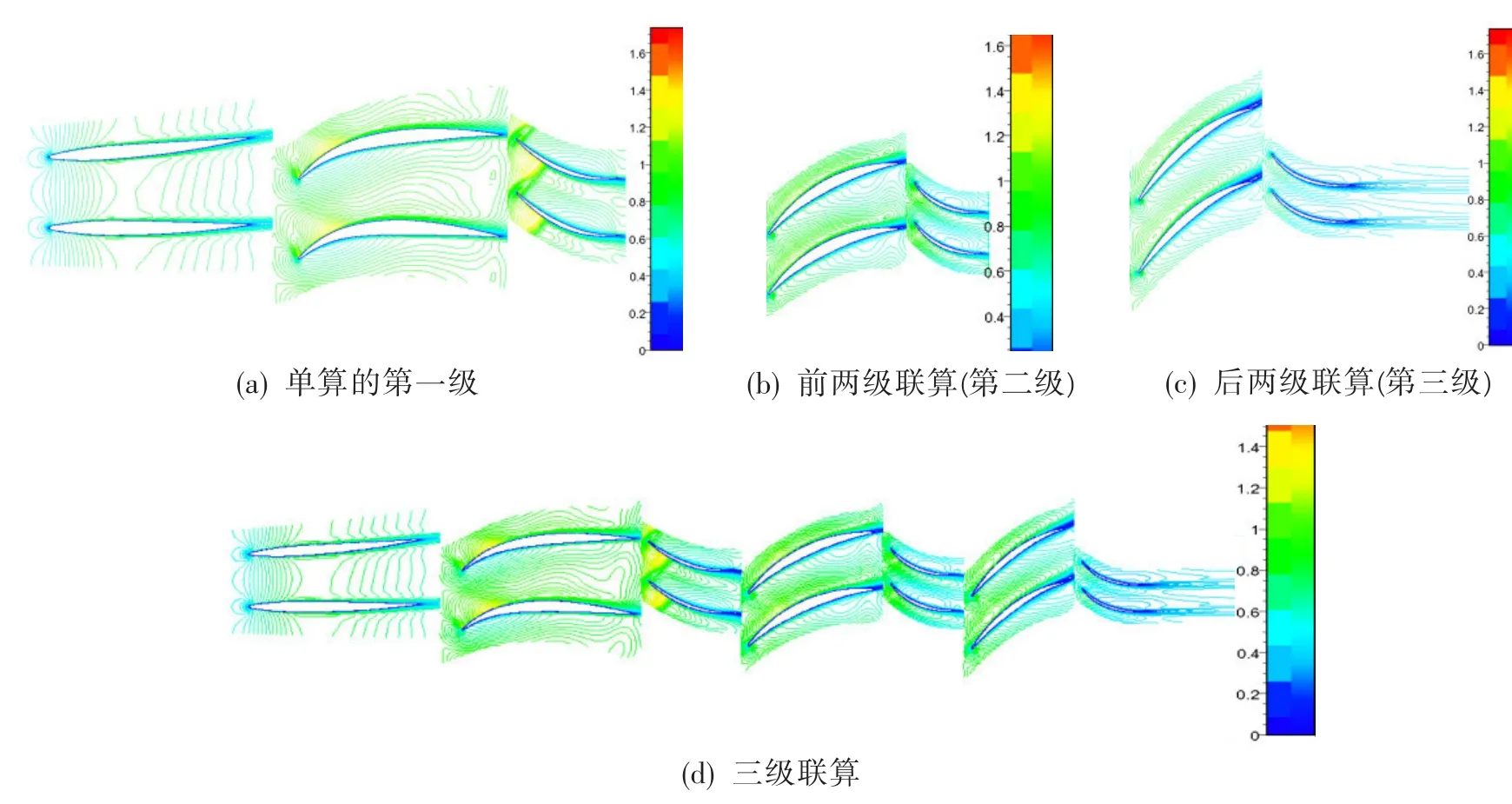
圖2 5%徑向位置葉片槽道馬赫數(shù)等值線圖Fig.2 Relative Mach number isolines at 5%span of blade

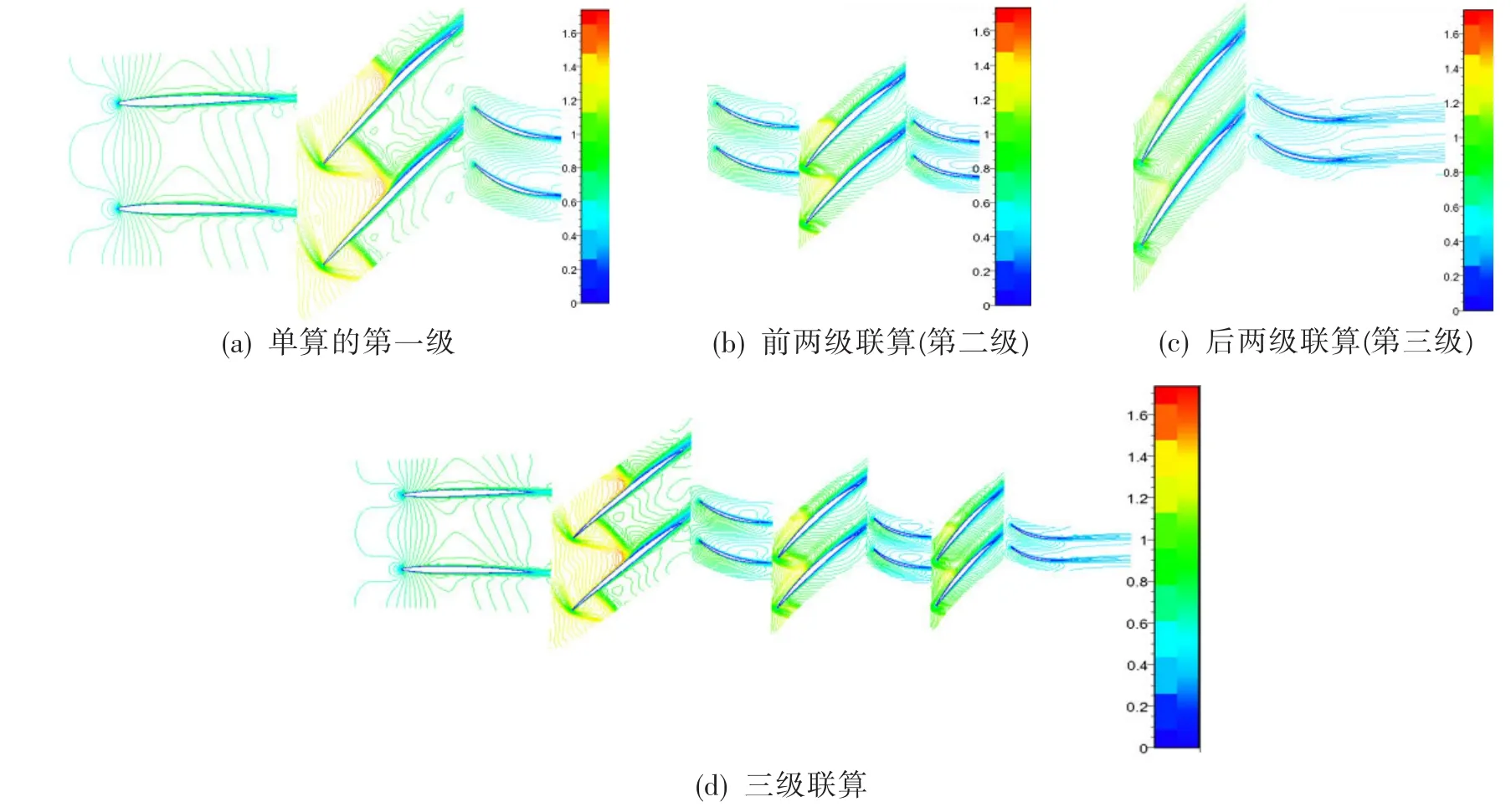
圖3 50%徑向位置葉片槽道馬赫數(shù)等值線圖Fig.3 Relative Mach number isolines at 50%span of blade

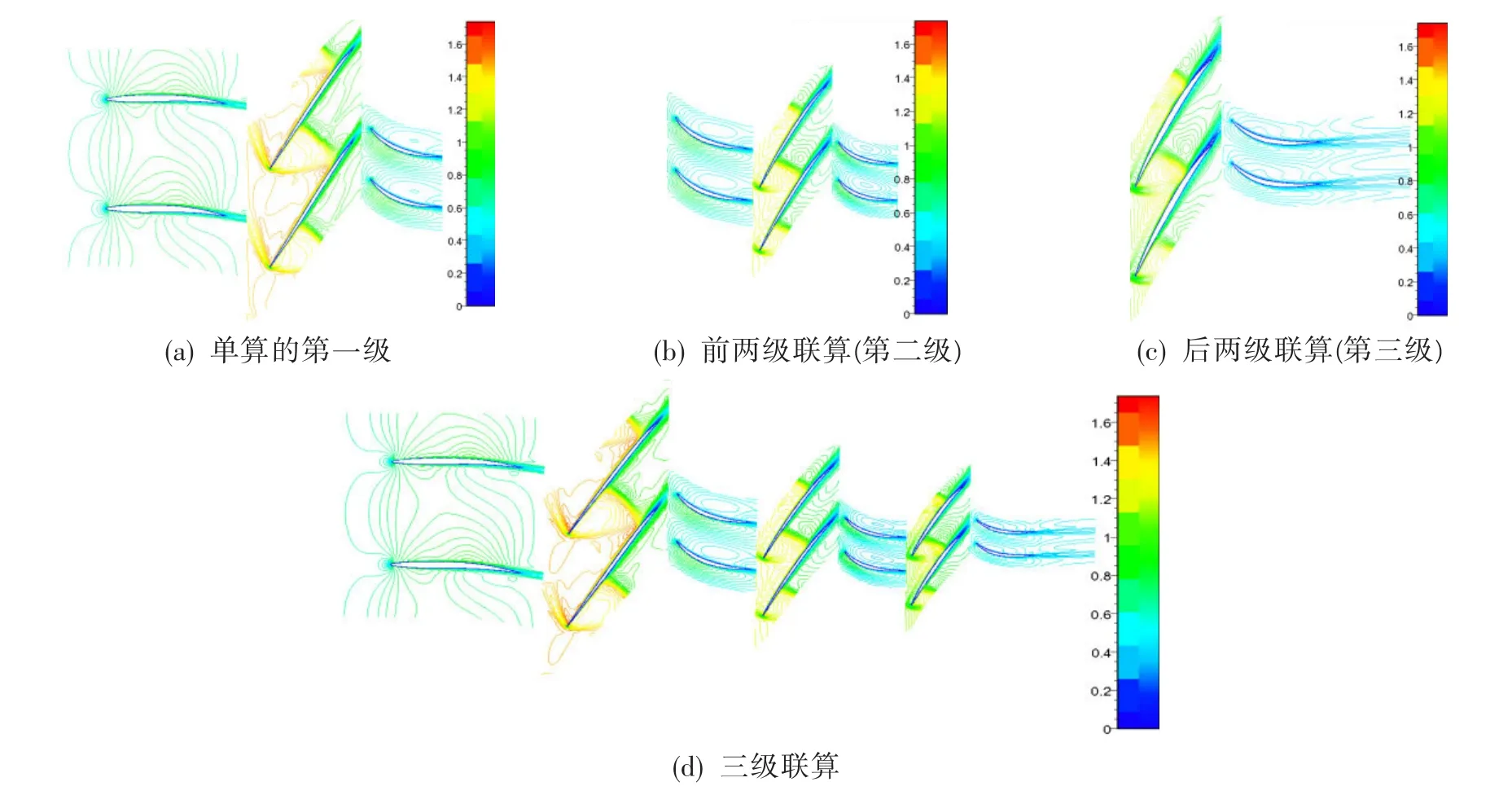
圖4 95%徑向位置葉片槽道馬赫數(shù)等值線圖Fig.4 Relative Mach number isolines at 95%span of blade

從圖2中可看出，采用該方式計算的各級流場分布和三級聯(lián)算各級根部流場分布基本一致：在轉(zhuǎn)子葉片排的根部截面，由于葉型較厚，氣流在葉背加速較明顯，但由于根部進(jìn)口馬赫數(shù)較低，葉片排前緣加速并未在槽道內(nèi)形成強(qiáng)激波，轉(zhuǎn)子的根部加功平穩(wěn)，最高馬赫數(shù)點基本上都出現(xiàn)在喉道位置。第一級靜子入口附近產(chǎn)生超音泡，局部區(qū)域氣流出現(xiàn)超聲現(xiàn)象；在二、三級靜子葉片排的根部截面，氣流經(jīng)前緣加速后很快達(dá)到最高速度點，由于葉柵通道中的擴(kuò)壓段較長，逆壓梯度小，氣流在靜子葉柵通道中平緩減速增壓。

從圖3中可看出，葉片中部各級流場分布和三級聯(lián)算的中部流場分布基本相同：第一級轉(zhuǎn)子中部截面，氣流經(jīng)加速在葉片槽道的進(jìn)口處產(chǎn)生一道斜激波，在葉片槽道中下游產(chǎn)生一道正激波。

從圖4中可看出，葉片尖部各級流場分布和三級聯(lián)算的尖部流場分布差別很小：轉(zhuǎn)子的尖部截面，葉型彎角較小，氣流在吸力面上加速很小，但由于進(jìn)口馬赫數(shù)很高，氣流在轉(zhuǎn)子葉片槽道進(jìn)口處產(chǎn)生了一道斜激波，在葉片槽道中下游產(chǎn)生一道正激波。靜子葉片排的尖部截面，氣流經(jīng)過前緣加速后很快達(dá)到最高速度點，這是由于葉柵通道中的擴(kuò)壓段較長，逆壓梯度小，從整體上看，氣流均勻減速增壓；轉(zhuǎn)子葉片尖部的間隙流、二次流對后面排靜子葉片的影響不明顯。

圖5為各單級對應(yīng)位置的葉片表面靜壓分布與整個風(fēng)扇部件聯(lián)算時的對比圖。從圖中看：采用該方式得到的各單級表面靜壓分布與所有級聯(lián)算對應(yīng)級的表面壓力分布基本重合，用此來評估各級性能參數(shù)，結(jié)果能較真實地反映其在整個部件中的氣動性能。從整個計算耗時來看，該方式計算的單級耗時相當(dāng)于三級聯(lián)算的三分之一，若部件級數(shù)更多，其優(yōu)勢將會更大。另外，在進(jìn)行風(fēng)扇/壓氣機(jī)部件設(shè)計時，該方式可多人多平臺同時設(shè)計，提高設(shè)計效率。

3.2 壓氣機(jī)計算結(jié)果分析

取某七級壓氣機(jī)的第三級和第四級進(jìn)行聯(lián)算，并將第四級的結(jié)果與整機(jī)三維計算得到的結(jié)果進(jìn)行對比。圖6示出了葉片根部、中部和尖部靜壓分布對比情況，可見，三、四級聯(lián)算得到的第四級壓氣機(jī)葉片徑向各截面的靜壓分布，與整機(jī)三維計算得到的結(jié)果基本一致。

4 結(jié)論

(1)采用第一級、前兩級、后兩級聯(lián)算得到的各單級性能參數(shù)和流場細(xì)節(jié)，與風(fēng)扇整個部件聯(lián)算結(jié)果吻合度較高，可用此方法設(shè)計各級性能。

(2)對壓氣機(jī)中的兩級進(jìn)行聯(lián)算得到的后一級流場分布，與壓氣機(jī)整機(jī)聯(lián)算的結(jié)果基本一致。

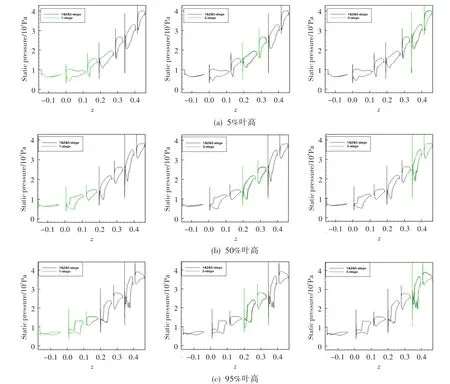
圖5 不同徑向位置葉片表面的壓力分布Fig.5 Blade static pressure distribution at different spans

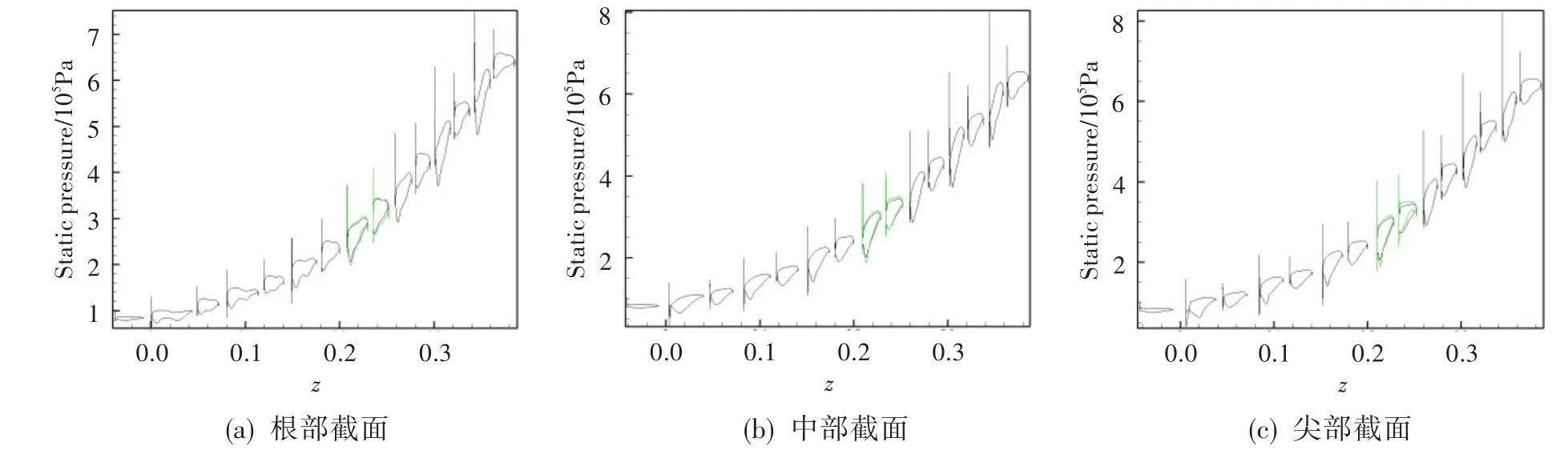
圖6 不同截面葉片表面的壓力分布Fig.6 The comparison of surface static pressure distribution at different sections

(3) 在進(jìn)行多級風(fēng)扇/壓氣機(jī)方案設(shè)計時，可采用兩級聯(lián)算的方法對后一級性能進(jìn)行評估和改進(jìn)設(shè)計。采用此方法能提高設(shè)計效率，縮短設(shè)計周期，且風(fēng)扇/壓氣機(jī)級數(shù)越多，其優(yōu)勢越大。

[1]朱方元.航空軸流葉片機(jī)氣動設(shè)計[M].北京：航空專業(yè)教材編審組，1984.

[2]北京航空航天大學(xué)能源與動力工程學(xué)院流體機(jī)械系.葉輪機(jī)原理講義[M].北京：北京航空航天大學(xué)，2008.

[3]Robbins W H，Dugan J F.Prediction of Off-Design Perfor?mance of Multi-Stage Compressors[R].NASA SP-36，1965.

[4]Klapproth J F，Miller M L，Parker D E.Aerodynamic De?velopment and Performance of the CF6-6/LM2500 Com?pressor[R].AIAA 1979-7030，1979.

[5]Soltani M R，Ghofrani M B，Khaledi H，et al.Optimum De?sign and Sensitivity Analysis of Axial Flow Compressor with Combination of Analytical Method,Qualitative and Quantitative Rules and Genetic Algorithm[R].ASME GT2008-51033，2008.

[6]曲愛民.某型多級壓氣機(jī)三維流場分析[J].汽輪機(jī)技術(shù)，2006，48(2)：98—100.