直冷卻通道斜置肋片傳熱特性的數值研究

張艾萍，付 磊，杜五一

(東北電力大學能源與動力學院，吉林 長春 132012)

1 引言

燃氣輪機中，隨著輪前燃氣溫度的提高，渦輪葉片承受的熱傳導也隨之增大，嚴重影響渦輪運行的安全性和穩定性。改進渦輪葉片的冷卻方式和冷卻結構，以滿足渦輪穩定運行的要求，是解決葉片受熱問題的主要手段之一。而掌握冷卻通道傳熱分布規律，進而改進和優化葉片內部冷卻通道結構，對提高葉片受熱能力具有重要意義。

對于加置肋片、強化換熱，很多學者都做了大量的實驗研究和數值模擬。Han等[1]對有周期性肋片的矩形直通道中的換熱與流動性能進行了實驗研究，發現方形通道中肋片斜置角度α為30°～45°時的換熱效果比橫肋的換熱效果提高約30%。Park等[2]研究了五種不同寬高比的情況，對于方形通道，當肋片斜置角度為45°時有最好的強化換熱效果。Hsieh等[3]研究了方形帶肋直通道的換熱效果，并給出了努賽爾數與雷諾數之間的經驗關系式。Stephens等[4]研究了斜肋對換熱效果的影響，發現換熱效果受肋的角度等參數和主流雷諾數的影響。Ooi等[5]用v2-f、k-ε、S-A模型模擬了內部有橫置肋片的直通道，發現v2-f模型的計算結果更接近實驗數據，但不能很好地預測不帶肋壁面的傳熱情況。Amano等[6]用k-ε、k-ω兩種湍流模型，對靜止條件下帶擾流肋的渦輪冷卻通道進行了數值計算，并與實驗結果進行對比，發現k-ε模型的計算結果與實驗數據較吻合。Slabaugh等[7]對設有單邊擾流肋片的窄通道進行了數值研究，表明阻塞比增大，換熱效果提高，但隨之流動損失增大。

本文以擾流通道為原始模型，在定雷諾數下，利用CFX軟件對不同斜置角度下的原始模型進行模擬，并將所得數據輸入自行編寫的MATLAB程序尋優，以研究定雷諾數下，斜置肋片角度與帶肋直冷卻通道整體換熱效果和綜合換熱性能的相關情況。

2 模型與尋優

數值模擬使用以有限體積法和隱式方法求解三維穩態N-S方程組的CFX軟件。求解過程中，選用二階精度的差分格式，計算殘差設定在10-5以下收斂。湍流模型選用k-ε模型和自動壁面函數處理方式。利用MATLAB程序運算，得出帶肋壁面最大整體換熱效果下的肋片斜置角度和綜合換熱性能最優時的肋片斜置角度。

2.1 幾何模型與邊界條件

幾何模型以Han等[1]的帶肋直冷卻通道作為原始計算模型，見圖1。該模型的通道橫截面為正方形，其上下壁面分別設置有10個截面為方形的橫置肋片，肋高e=2.38125 mm，肋高與當量直徑D之比為0.047：1，肋高與肋間距P之比為1：10，直通道截面高H與肋寬W之比為1：1，雷諾數Re取定值10000。

圖1 原始計算模型的結構Fig.1 The structure of the original model

為減少計算模型的整體網格數量以節省計算時間，提高重點關注區域的計算精度，根據CFX軟件功能，對原始計算模型進行了改造，采用具有對稱性的帶肋直通道模型，如圖2所示。

圖2 改造后的計算模型結構Fig.2 Reconstructed calculation model

計算模型邊界條件：進口設置為速度進口，給定Re=10000時相對應的法向速度，出口設置為靜壓101325 Pa，帶肋壁面和兩側光滑壁面給定熱流密度定值q，頂面設置為直通道對稱面。

計算模型采用結構化六面體網格形式，在各肋之間的重點求解區域局部加密，其它部分與直通道計算模型的整體網格密度相同。求解模型帶肋壁面的距壁面距離的無量綱值均小于2，滿足模型計算要求。圖3示出了內部斜置角度60°肋片的直冷卻通道網格。

圖3 斜置角度為60°的網格示意圖Fig.3 Grid map of oblique angle of 60 degrees

2.2 尋優

2.2.1 不同斜置角度下的整體換熱效果

衡量換熱效果的好壞通常引用努賽爾數來表示。直冷卻通道的換熱系數h和努賽爾數Nu的定義分別為：

式中：λ為冷卻空氣的傳熱系數；TW為通道的壁面溫度；Tf為參考溫度，文中取進口冷卻空氣的平均溫度為參考溫度。

對直通道內部肋片的斜置角度從30°至60°以5°為等差，劃分為7種工況，分別進行相同邊界條件下的數值模擬，并以所得帶肋壁面的平均努賽爾數和斜置角度輸入MATLAB程序尋優。通過CFX后處理軟件CFD-Post中的面積加權均值法求得。運算結果如圖4所示，當α=48.62°時，----Nu=139.566，帶肋壁面的----Nu最大，整體換熱效果最好。

圖4 斜置角度與帶肋壁面平均努賽爾數的擬合曲線Fig.4 Fitted curve of α and----Nu

2.2.2 不同斜置角度下的綜合換熱性能

在直通道內部流動模擬過程中，以實際流動損失與完全湍流發展時光滑管道的流動損失之比來表示流動損失情況，有：

式中：Pin為進口壓力，Pout為出口壓力，L為直通道計算模型的長度，G為進口冷卻空氣的質量流量，Re=10000。

綜合考慮換熱效果和流動損失對直通道整體換熱性能的影響，綜合換熱系數N的表達式為：

將綜合換熱系數與斜置角度代入程序進行擬合，結果見圖 5。可見，當α=30.34°時，N=1.664，帶肋直通道的綜合換熱性能最好。

3 計算與驗證結果分析

3.1 湍流模型結果

圖5 斜置角度與綜合換熱系數的擬合曲線Fig.5 Fitted curve ofαandN

分別采用k-ε、k-ω和SST湍流模型，對直冷卻通道的換熱與流動特性進行數值模擬，并將其結果與Han等[1]的實驗數據進行對比。由圖6可看出，k-ω和SST湍流模型的模擬結果明顯小于實驗數據，其偏差過大；而k-ω湍流模型所得結果與實驗數據吻合較好，能很好地(定性和定量)反映直冷卻通道的整體換熱效果。下文中模擬結果均采用k-ε湍流模型得到。

圖6 不同湍流模型帶肋壁面肋間努賽爾數與實驗數據的對比Fig.6 Nuvs.experimental data of different turbulence model

3.2 不同斜置角度下的整體換熱效果

對于通過MATLAB程序運算得出的結果，須經CFX軟件進行同等條件下的數值模擬，以印證程序尋優結果。結果表明，當α=48.62°時，----Nu=139.562，其帶肋壁面的----Nu與尋優結果的差值小于0.005，尋優結果可信度很高。

圖7很好地展示了不同斜置角度下帶肋壁面的換熱效果。可見，α=48.62°時，----Nu最大，其換熱效果明顯比其它角度下的好，其肋頂端的高換熱區域幾乎全部被覆蓋，肋間壁面的高換熱區域影響也最大，覆蓋面積也最廣；α=90°時，整體換熱效果最差。

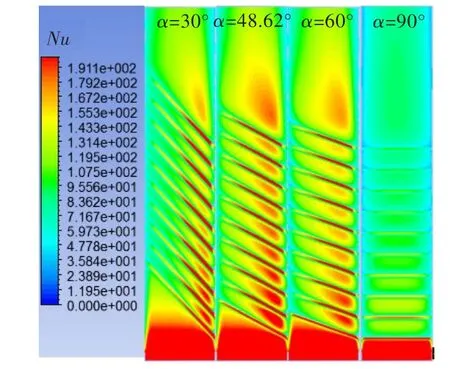
圖7 不同斜置角度下帶肋壁面的努賽爾數云圖Fig.7 Nucontour of ribbed surface of differentα

圖8 不同斜置角度下肋間壁面的努數比值Fig.8 grid figure of wall between the ribs of differentα

圖8示出了不同斜置角度下肋間壁面的換熱效果。可見，當α=48.62°時，肋間壁面的努數比最大，整體換熱效果最好，并且沿冷卻流體的總流動方向，各肋間壁面的換熱效果相差不大，其平均換熱效果更加理想；α為30°和60°時，各肋間的努數比差值較小，平均換熱效果也較好，但努數比值均比α=48.62°時的低；α=90°時，肋間壁面的換熱效果浮動較大，導致帶肋壁面冷卻不均現象比較嚴重。

3.3 不同斜置角度下的綜合換熱性能

對于帶肋直冷卻通道綜合換熱性能，需綜合考慮直通道的流動損失和整體換熱效果。

從圖9中不同斜置角度下的流動損失可看出，30.34°斜置肋片產生的流動損失最小，45°和 90°斜置肋片引起的流動損失相差不大，60°斜置肋片導致的流動損失最大。

圖10展示了不同斜置角度下的綜合換熱系數。可見，30.34°斜置肋片直冷卻通道的綜合換熱性能最好，N=1.664；30°斜置肋片的綜合換熱性能(N=1.662)與 30.34°的基本相同，可認為 30°斜置肋片直冷卻通道的綜合換熱性能最好；45°、60°斜置肋片的綜合換熱系數均比30°時的低。

圖9 不同斜置角度下的流動損失Fig.9 Flow loss of differentα

圖10 不同斜置角度下的綜合換熱系數Fig.10 Integrated heat transfer coefficient N of differentα

4 結論

(1)帶肋直通道在定雷諾數下，肋片的斜置角度與整體的換熱特性呈近似拋物線關系，綜合換熱性能與斜置角度呈近似對數關系。

(2)內設48.62°斜置肋片的直冷卻通道換熱能力最強，換熱效果最佳，且冷卻平均度較其它角度有更大的優勢；90°橫置肋片的換熱效果最差。

(3)直冷卻通道內設30°斜置肋片的結構產生的流動損失最小，其綜合換熱性能最好，且大大優于其它角度。

[1]Han J C，Park J S，Ibrahim Y M.Measurement of Heat Transfer and Pressure Drop in Rectangular Channels with Turbulence Promoters[R].NASA CR-4015，1986.

[2]Park J S，Han J C，Huang Y，et al.Heat Transfer Perfor?mance Comparisons of Five Different Rectangular Chan?nels with Parallel Angled Ribs[J].International Journal of Heat and Mass Transfer，1992，35(11)：2891—2903.

[3]Hsieh S S，Hong Y J.Heat Transfer of Air Channel Flow over Repeated Ribs with Staggered Type Configuration[R].AIAA 89-0426，1989.

[4]Stephens M A，Shih T I P，Civinskas K C.Effects of In?clined Rounded RIBS on Flow and Heat Transfer in a Square Duct[R].AIAA 95-2115，1995.

[5]Ooi A，Iaccarino G，Durbin P A，et al.Reynolds Averaged Simulation of Flow and Heat Transfer in Ribbed Ducts[J].International Journal of Heat and Fluid Flow，2002，23(6)：750—757.

[6]Amano R S，Guntur K，Lucci J M.Computational Study of Heat/Mass Transfer Characteristics in a Ribbed Cooling Channel in a Stationary Gas Turbine Blade[R].AIAA 2009-4520，2009.

[7]Slabaugh C D，Valentino M，Ricklick M，et al.Heat Trans?fer and Friction Augmentation in a Narrow Rectangular Ductwith Ribs Applied to One Wall[R].AIAA 2010-6952，2010.