無人機液壓彈射系統的模型研究與仿真

趙灼輝，吳素珍

(1.四川電力職業技術學院，四川成都610000;2.河南工程學院，河南鄭州451191)

伴隨著無人機在社會各領域中的廣泛應用，與之配套的彈射裝置也得到了長足的發展，蓄能器供油式無人機液壓彈射系統因具有可靠性高、反應速度快等特點，常被用于彈射中小型無人機［1］。

以往在對類似系統進行建模時，增速機構常被忽略，而這會對分析系統性能的精確性造成一定的影響。文中提出一種分析滑輪組模型的新方法，并利用功率鍵合圖法得到了無人機液壓彈射系統的數學模型，通過對一實際系統進行仿真，得到了一些有益的結論。

1 無人機液壓彈射系統工作原理

無人機液壓彈射系統的工作原理簡圖如圖1所示，系統主要由液壓能源系統、控制元件、彈射架、增速機構、無人機及滑車系統和緩沖裝置等組成。系統工作過程可分為4 個階段，文中主要研究系統的彈射階段。

彈射階段，閥2、6 通電，液控單向閥5 反向開啟，蓄能器和液壓泵中油液進入液壓缸無桿腔，驅動活塞桿低速運動，經滑輪組增速后，鋼絲繩帶動無人機及滑車實現高速運動，當滑車加速到彈射架指定位置時，行程開關動作，閥2 斷電，閥8 反向關閉，無人機脫離滑車起飛，系統進入緩沖階段。

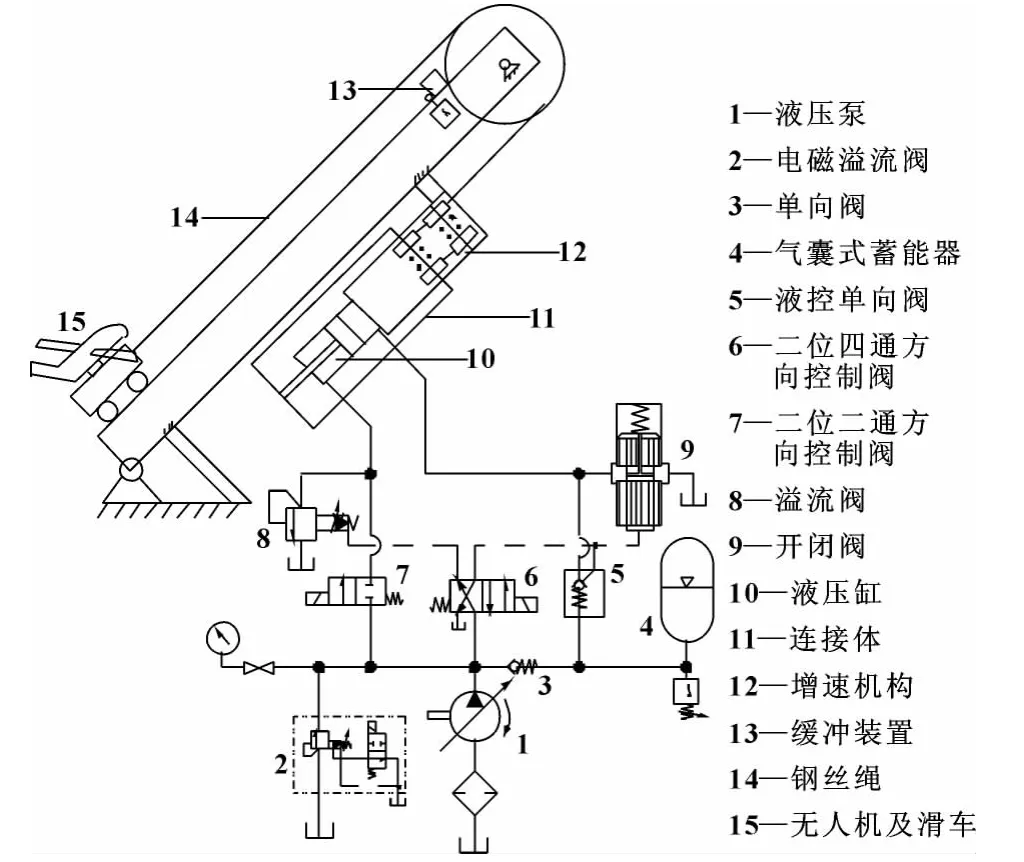
圖1 無人機液壓彈射系統工作原理簡圖

2 無人機液壓彈射系統模型的簡化

2.1 增速機構模型的簡化

增速機構由動滑輪組、定滑輪組和鋼絲繩等組成，圖2 為增速倍數n為偶數的增速滑輪組力學模型，若需n為奇數，則在鋼絲繩末端繞過最后一個定滑輪后，將其固定在動滑輪組上［2］。

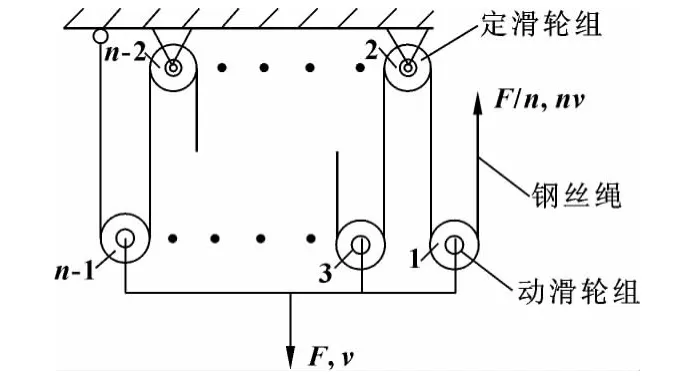
圖2 增速滑輪組力學模型

文中對滑輪組模型作如下考慮:

(1)考慮到鋼絲繩的伸縮，可將鋼絲繩看作彈性很小的彈簧，將鋼絲繩與滑輪、滑輪軸承處的摩擦看作阻性元;

(2)將滑輪組間2n段鋼絲繩按并聯規則等效;

(3)將活塞桿、連接體、動滑輪組和動滑輪組轉換的質量體合并為m1;定滑輪組轉換的質量體為m2，無人機及滑車的質量為m3。

(4)因對滑輪組和鋼絲繩進行了等效，故在簡化模型中用杠桿來表示增速關系。

2.2 液壓系統的簡化

為了簡化模型，對液壓系統作以下處理［3］:

(1)合并了軟管和液壓缸的液容、軟管和閥口的液阻;

(2)相對于蓄能器，液壓泵的流量較小，因此忽略了液壓泵所在管路的液阻和液容。

2.3 無人機液壓彈射系統的簡化模型

根據以上分析，可得無人機液壓彈射系統的簡化模型如圖3所示。

圖3 無人機液壓彈射系統簡化模型

3 無人機液壓彈射系統數學模型建立

3.1 無人機液壓彈射系統的數學模型

功率鍵合圖，簡稱鍵合圖，是一種用來描述工程系統能量結構的圖示表示方法，是進行液壓系統乃至各類工程動態特性仿真時有效的建模工具［4］。

根據無人機液壓彈射系統簡化模型及鍵合圖建模的有關規則［5］，建立了如圖4所示的無人機液壓彈射系統的鍵合圖模型。模型中狀態變量有:蓄能器容積的變化V1，液壓缸進油腔容積的變化V9，液壓缸出油腔容積的變化V18，質量體m1的動量P12，質量體m2的動量P24，無人機及滑車的動量P31，等效鋼絲繩的變形X20，連接滑車鋼絲繩的變形X27。

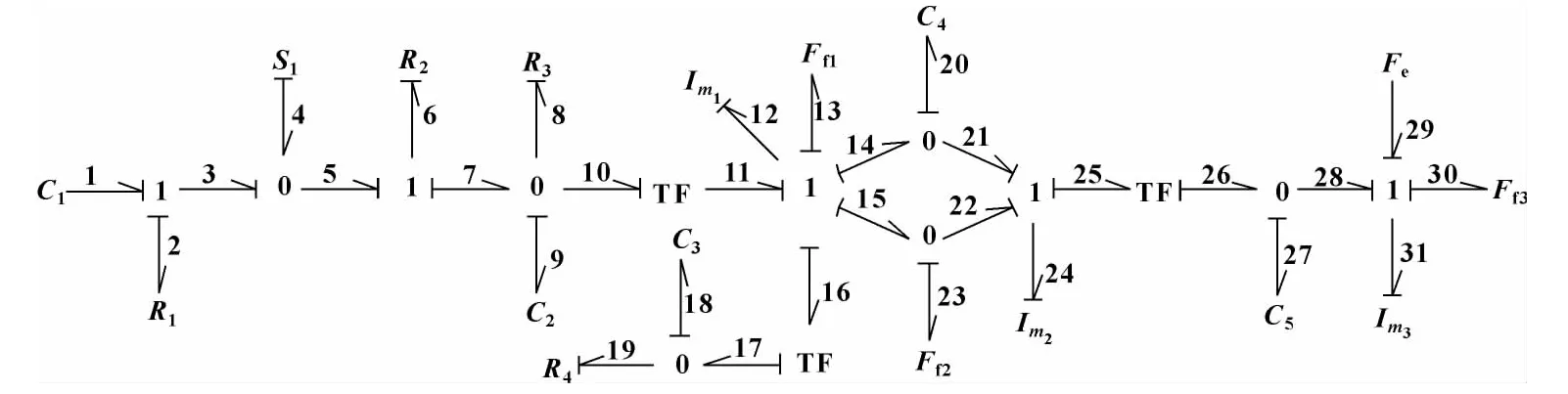
圖4 無人機液壓彈射系統鍵合圖模型

依據鍵合圖模型，可推導出下列狀態方程:

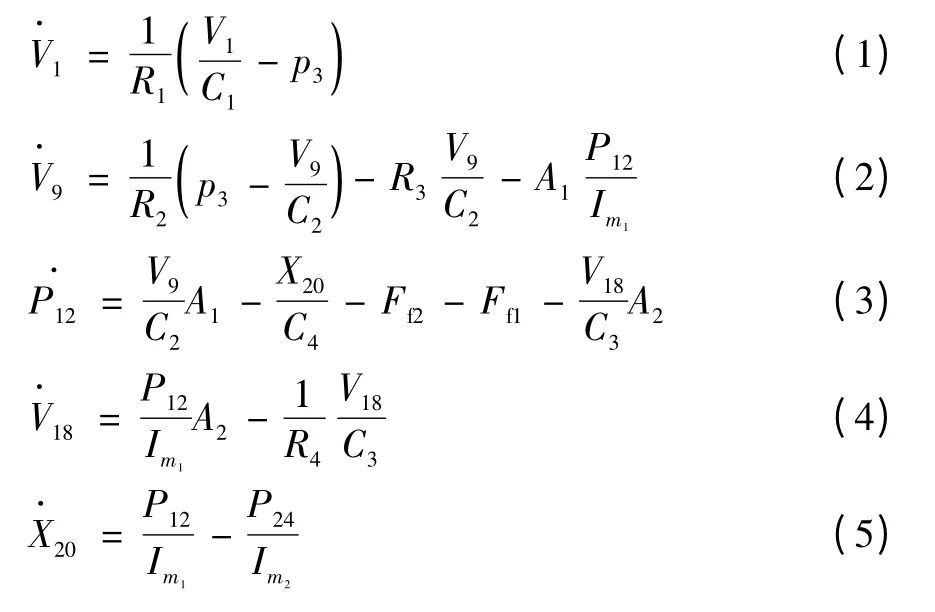
其中:

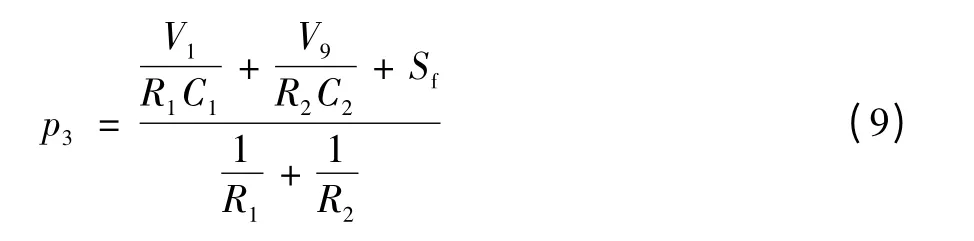
式中:p3為蓄能器出口壓力;Sf為液壓泵流量;C1為蓄能器的容性;C2為液壓缸進油腔和進油管道液容之和;C3為液壓缸出油腔和出油管道液容之和;C4為等效鋼絲繩的容性;C5為連接滑車鋼絲繩的容性;R1為蓄能器出口液阻;R2為液控單向閥液阻和進油管道液阻之和;R3為自制開閉閥的泄漏液阻;R4為出油管道液阻和溢流閥液阻之和;Ff1為液壓缸活塞處摩擦力;Ff2為滑輪組中總摩擦力;Ff3為無人機及滑車所受阻力;Fe為無人機自身動力;Ⅰm1為m1的質量;Ⅰm2為m2的質量;Ⅰm3為m3的質量;A1為液壓缸進油腔面積;A2為液壓缸出油腔面積;n為滑輪組增速比。

3.2 數學模型參數的確定

(1)蓄能器供油模型

蓄能器的工作過程可按絕熱過程處理，依據絕熱過程氣體狀態方程可得［6］:

其中:

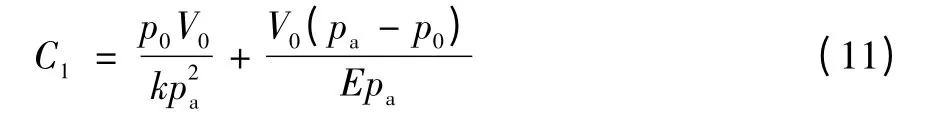
式中:p1為蓄能器內瞬時壓力;p0為蓄能器的充氣壓力;pa為蓄能器的充油壓力;V0為蓄能器的容積;q為蓄能器出口流量;k為氣體熵數;E為液壓油彈性模量。

(2)滑輪轉動的等效轉換

按照能量守恒的原則將滑輪的轉動轉換為定質量體的直線運動［7］:

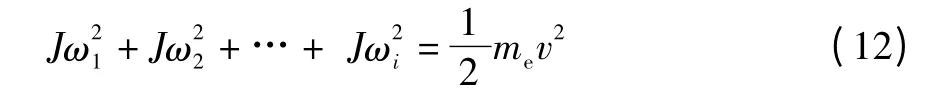
對定滑輪組:

對動滑輪組:

其中:J為滑輪的轉動慣量;ωi為動或定滑輪組中第i個滑輪的角速度;me為定質量體的質量;v為定質量體的速度。

4 無人機液壓彈射系統的仿真

采用變步長的四階龍格庫塔法，通過在MATLAB軟件上編寫仿真程序求解上述狀態微分方程組［8］。仿真系統的主要參數:蓄能器的容積為0.063 m3，蓄能器的充氣壓力為16 MPa，蓄能器的充油壓力為23 MPa，無人機及滑車質量為110 kg，無人機最小安全起飛速度為35 m/s，滑輪組增速比為20，液壓缸直徑為0.125 m，行程為0.6 m，彈射架導軌長為8 m，仿真時間為0.4 s。

無人機行程為6.4 m 時仿真結束，忽略緩沖階段的時間，可得液壓缸進油腔壓力變化曲線如圖5所示，無人機及滑車速度變化曲線如圖6所示。

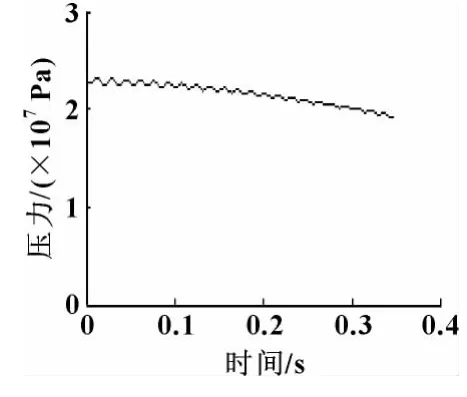
圖5 液壓缸進油腔壓力變化曲線

圖6 無人機及滑車速度變化曲線

由仿真可知:t=0.35 s 時，無人機的速度為35.6 m/s，滿足了無人機安全起飛的速度要求。通過與相關試驗類比，證明該研究方法是可行的。

5 結論

(1)提出了一種分析滑輪組模型的新方法，得到了無人機液壓彈射系統的簡化模型，為系統的進一步分析奠定了基礎。

(2)基于功率鍵合圖法建立了無人機液壓彈射系統的鍵合圖模型，推導出了模型的狀態微分方程;經過仿真與類比分析可知，功率鍵合圖法對研究該系統是有效的。

［1］國外無人機大全編寫組.國外無人機大全［M］.北京:航空工業出版社，2001:447-457.

［2］李悅，裴錦華.無人機氣液壓發射動力學數值仿真［J］.機械工程學報，2011，47(8):183-190.

［3］劉興陽，同智寬，李永林，等.無人機液壓彈射裝置能源系統仿真研究［J］.機床與液壓，2008，36(12):170-172.

［4］KARNOPP D，ROSENBERG Ronald C.System Dynamics:A Unified Approach［M］.NewYork:Wiley-Interscience，1990.

［5］王中雙.鍵圖理論及其在系統動力學中的應用［M］.哈爾濱:哈爾濱工程大學出版社，2000:19-60.

［6］嚴金坤.液壓動力控制［M］.上海:上海交通大學出版社，1986:1-35.

［7］趙俊波.取料系統起動特性及速度穩定性的理論分析和試驗研究［D］.鄭州:鄭州大學，2010:18-20.

［8］劉白雁.機電系統動態仿真［M］.北京:機械工業出版社，2005:108-111.