基于NSGAII的齒輪減速器多目標優化研究*
成曉升,余軍合,戰洪飛
(寧波大學機械工程與力學學院,浙江寧波 315211)
0 引 言
在工程設計中,多目標優化問題非常普遍,而且求解過程通常比較復雜,如何獲取這些問題的最優解,一直都是學術界和工程界研究的熱點。一般情況下,多目標優化問題的各個子目標之間是矛盾的,一個子目標性能的改善有可能會引起另外一個或幾個子目標性能的降低,要使全部子目標同時達到最優是不可能的,只能在它們中間進行協調和折中處理[1]。
許多學者對該類問題進行了研究。寧曉斌等[2]采用了多島遺傳法對評價汽車平順性和操穩性的性能指標進行優化,有效地解決了多目標之間的矛盾。N.Srinivas和 Kalyanmoy Deb[3]提出了 NSGAII,采用快速非占優排序,降低了計算復雜度;采用擁擠距離比較算子,保持了種群的多樣性;引進精英策略,擴大采樣空間,防止優良個體的丟失,提高了運算速度和魯棒性。
本研究基于擁擠距離的非占優排序方法,研究多約束、離散變量的處理方法;通過修改和調試NSGAII算法,以二級減速器的設計為例進行多目標優化設計,對優化結果進行對比分析,為多目標優化問題的求解提供參考。
1 多目標優化問題描述
多目標優化問題的數學形式可以如下描述[4]:
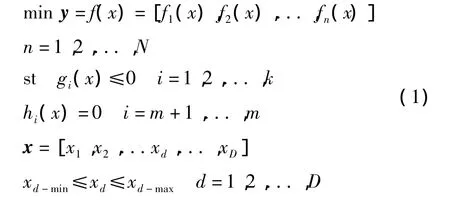
式中:x—D維決策向量;y—目標向量;N—優化目標總數;gi(x)≤0—不等式約束;hj(x)=0—等式約束;fn(x)—目標函數;xd-min,xd-max—每個變量的上、下限。
2 改進的非占優排序遺傳算法
改進的非占優排序遺傳算法(Non-Dominated Sorting in Genetic Algorithms II,NSGAII)的主要步驟包括:初始化種群、目標函數計算、非占優排序、選擇操作、遺傳和變異操作、種群替換策略和得到帕累托前沿[5]。本研究主要介紹基于擁擠距離的非占優排序方法,提出約束和離散變量的處理方法。
2.1 基于擁擠距離的非占優排序
基于擁擠距離的非占優排序包括:種群個體的非占優排序、擁擠距離的計算。
(1)非占優排序。即對種群中的所有個體進行兩兩比較。占優的個體相對其他個體而言,具有更低的非劣級別;互不占優的個體,具有相同的非劣級別。非占優序如圖1所示[6]。
(2)擁擠距離的計算。先將所有染色體在某一目標函數值上從小到大進行排序。處于該排序中的某個染色體在這一目標函數上的擁擠距離,為前一個染色體與后一個染色體在該目標函數值上之差;而該染色體的擁擠距離為該染色體在所有目標函數上對應的擁擠距離的總和[7]。
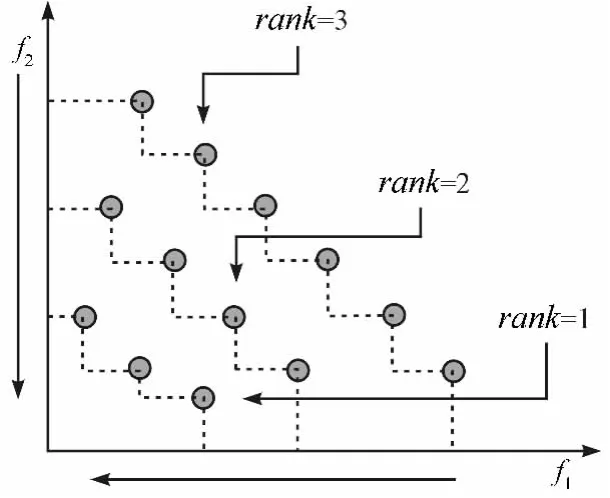
圖1 非占優排序
2.2 約束的處理
對于約束的處理,傳統的方法是采用懲罰方法。該方法的基本思想是設法對個體違背約束條件的情況給予懲罰,并將該懲罰體現在適應度函數設計中[8]。針對多目標多約束優化問題,本研究采用基于擁擠距離的非占優排序的方法,方法如下:
首先,定義解的約束違反量:
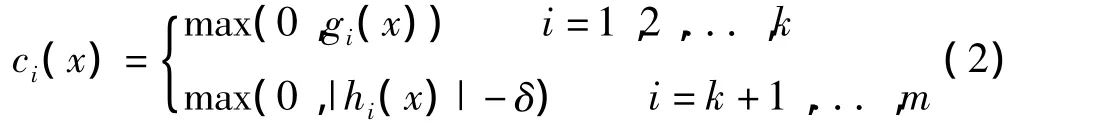
式中:δ—所允許的誤差值。
然后,計算總的約束違反量,計算公式為:
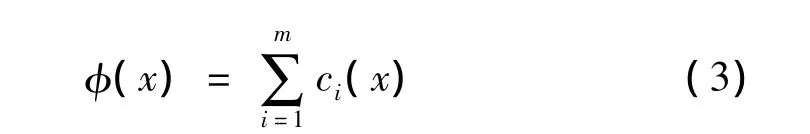
最后,根據兩個解的約束違法總量和目標函數值進行占優排序。遵循的規則是:
(1)(φ(x1)=0∧φ(x2)=0)∧(f(x1)<f(x2))?x1?x2
<表示占優;即當兩個解都滿足約束時,目標函數值小的占優;
(2)(φ(x1)=0∧φ(x2)>0)?x1?x2;即當一個滿足約束,而另一個解不滿足約束時,滿足約束的解占優;
(3)(φ(x1)>0∧φ(x2)>0)∧(φ(x1)<φ(x2))?x1?x2;即當兩個解都不滿足約束時,約束違反量小的占優。
2.3 離散變量、整數變量的處理
在一些多目標優化問題中,變量并不都是連續的,可能存在離散變量和整數變量。如在齒輪減速器的齒數是整數變量,模數是離散變量。初始化之后產生的父代和交叉變異之后產生的子代,它們的變量的取值很可能不是可選的值,因此需要對這些變量進行處理。
(1)處理整數變量的方法是:
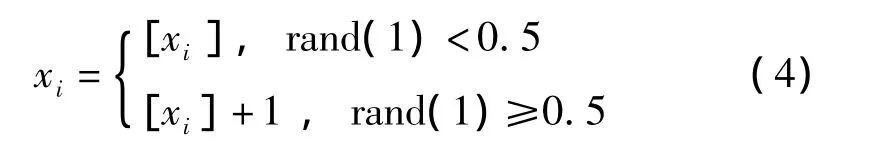
即采用隨機的方式,對整數變量的數值進行向上取整,或者向下取整。例如,某個整數變量初始化后的結果是20.2,取整的結果可能是20也可能是21,概率都是0.5。
(2)處理含非整數的離散變量,將離散變量的數值與所有可能取到的值放到一起進行排序,以隨機的方式選擇排序在前一位的數值還是后一位的數值。例如,某齒輪的模數可取的值為 2、2.5、3、3.5、4、4.5、5,在初始化后,如果值在4~4.5之間,處理的結果可能是4也可能是4.5,概率都是0.5。數學表達為:
如果4<xi<4.5,則:
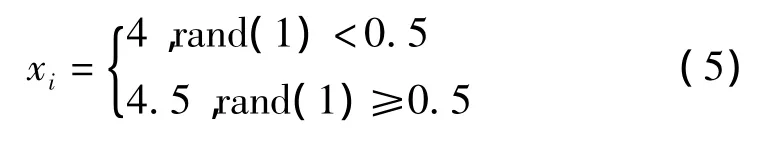
3 二級減速器的優化設計
由于齒輪的齒數是整數,模數是標準值,減速器的多目標優化設計,就是一個有約束的、有離散變量的多目標優化問題,本研究以二級斜齒輪減速器的優化設計為例來驗證所提方法是否可行。
3.1 建立多目標優化模型
本研究首先選擇合適的設計變量,然后建立目標函數,最后確定約束條件。
3.1.1 選擇設計變量
二級齒輪減速器的主體部分是兩對齒輪,選擇高速級的傳動比,小齒輪的模數、齒數、齒寬、螺旋角,作為設計變量。
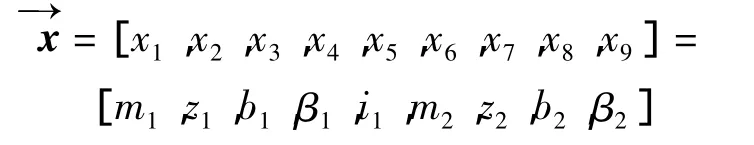
式中:m1,m2—離散變量;z1,z2—離散的整數變量,其他5個變量是連續變量。
3.1.2 建立目標函數
(1)減速器的體積:
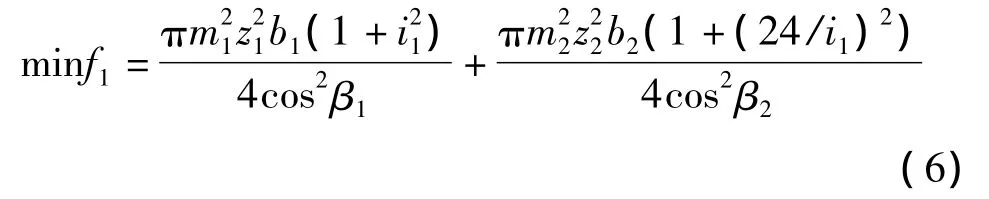
(2)減速器的可靠性。為了將目標統一為了取最小值,目標函數為減速器失效概率:
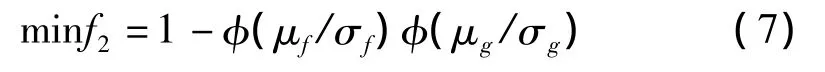
其中:
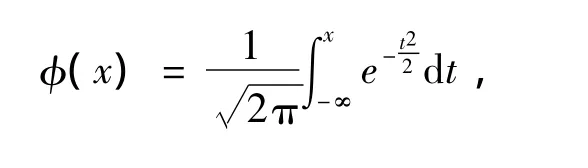
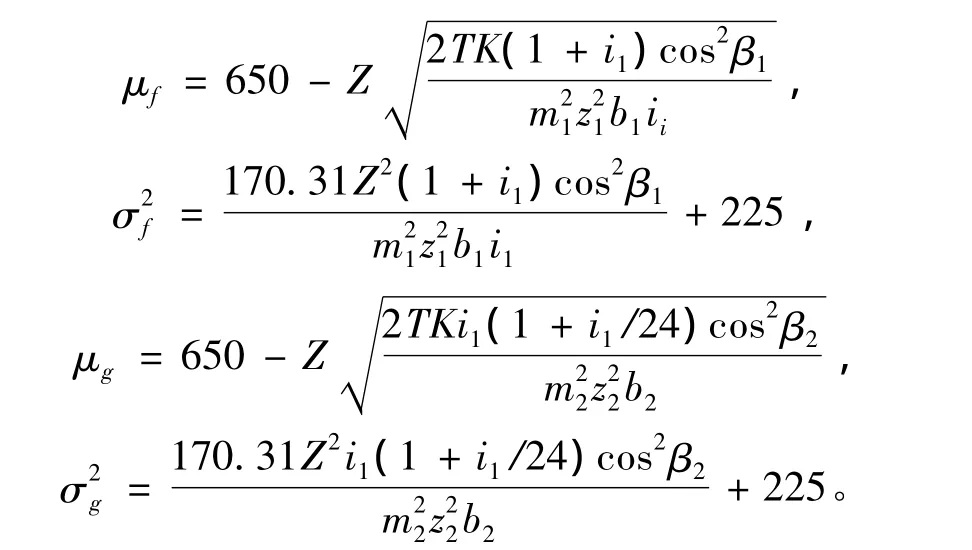
式中:[σ]H—齒輪齒面的接觸疲勞強度極限,T—輸入轉矩,K—載荷系數。
(3)減速器的轉角誤差:
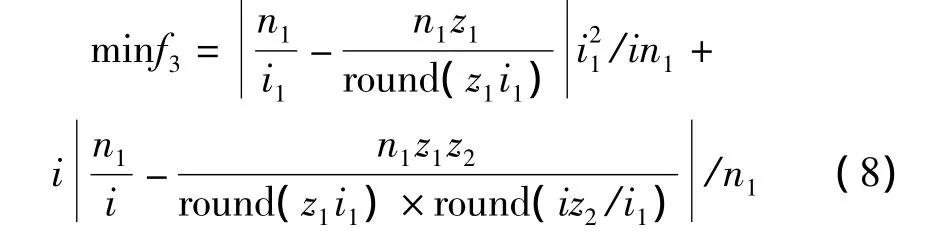
式中:i—總傳動比,round()—四舍五入成整數的操作,n1—高速軸的轉速。
3.1.3 確定約束條件
約束條件主要有齒面接觸疲勞強度條件、彎曲疲勞強度條件、大齒輪的最大浸油深度條件等[9-10]。(1)高速軸齒輪的接觸疲勞強度條件為:
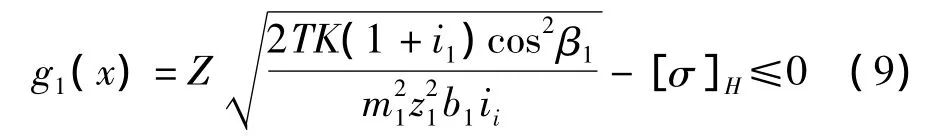
(2)低速的軸齒輪的接觸疲勞強度條件為:
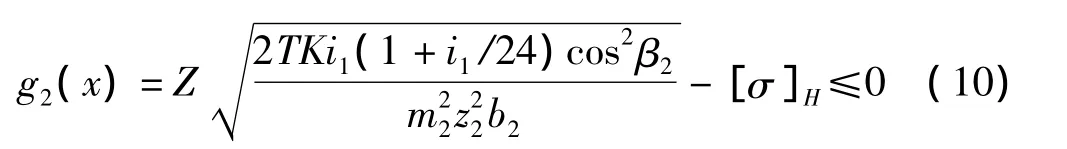
(3)高速軸齒輪的彎曲疲勞強度條件:
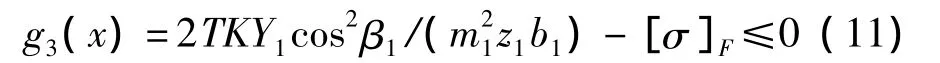
(4)低速的軸齒輪的彎曲疲勞強度條件為:
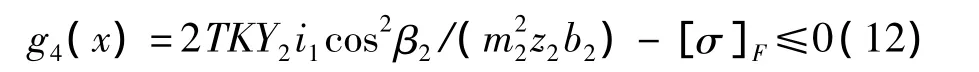
(5)大齒輪的最大浸油深度條件為:
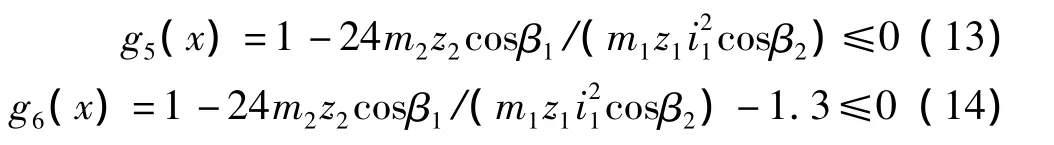
(6)高速級的大齒輪不與軸干涉的條件為:
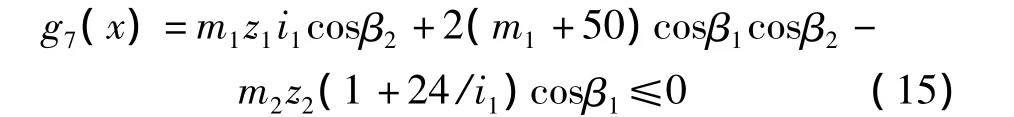
(7)設計變量的取值范圍:
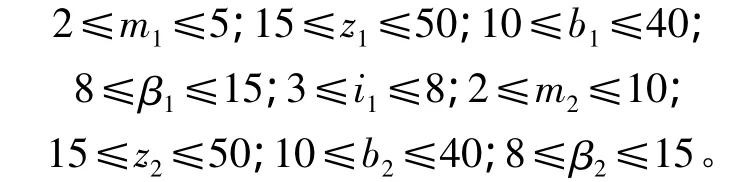
式中:Z—應力系數,[σ]F—齒輪齒面的彎曲疲勞強度極限,Y1—齒形系數,Y2—螺旋角系數。
3.2 多目標優化求解
某二級斜齒輪減速器的設計條件為:高速軸輸入功率P=6.2 kW;高速軸轉速n=1 450 r/min;總傳動比i=24;大齒輪材料為45鋼,正火HB187-207;小齒輪材料為45鋼,調質HB228-255。
本研究運用NSGAII對二級斜齒輪減速器的多目標優化模型進行優化求解,選擇初始種群數目為400,迭代次數為200,使用Matlab2010b運行程序,得到結果如圖2所示。從圖2中可看出,優化結果是一個三維的曲面,這是因為體積、失效概率和轉角誤差三者之間相互制約,從而得到帕累托曲面。
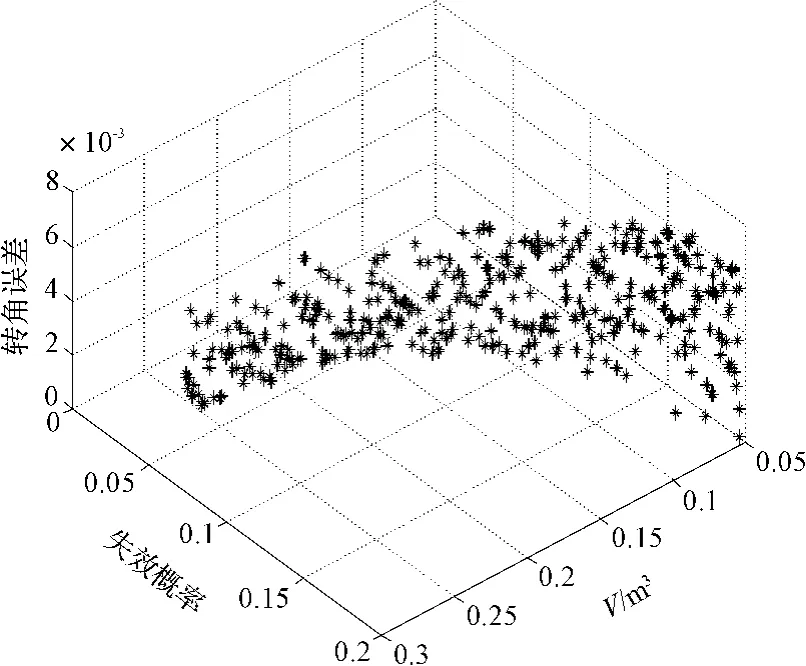
圖2 減速器多目標優化求解結果
為了能夠更好地觀察,現將這個三維的圖像投影成二維圖像,失效概率與體積如圖3所示。從圖3中可以很清楚地看到,體積與失效概率的二維圖像是一條光滑的曲線,這是因為體積和失效概率是相互制約的,從而得到帕累托曲線。
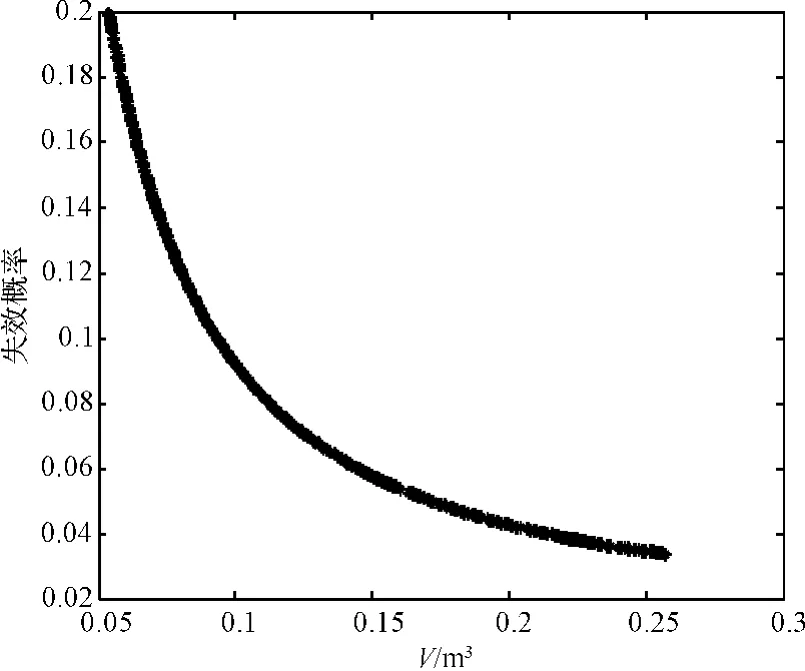
圖3 失效概率與體積
帕累托前沿中的解互不占優,根據目標重要程度,可以基于不同的準則,選擇不同的滿意解。本研究根據模糊集合理論的有關方法選取最優解。首先計算某個解在某個優化目標上,其目標函數值所占的比重,計算公式為:
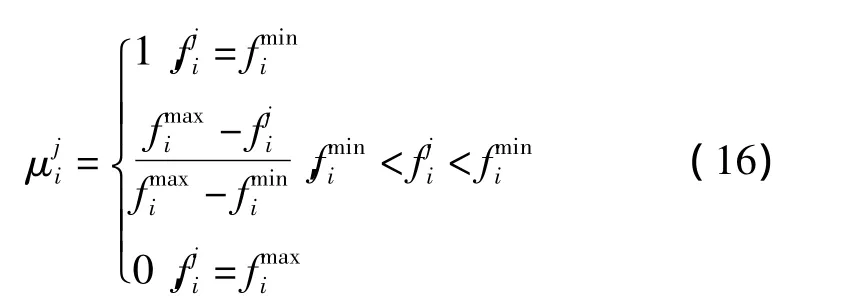
然后計算各個解在所有目標上所占的綜合比重。定義占優函數μi為某個解在所有目標上所占的綜合比重。占優函數值μi是一個居于0~1之間的數。占優函數值μi越大,表明對其評價的級別越高,亦即在客觀評價上用戶對此解更滿意,其計算公式為:
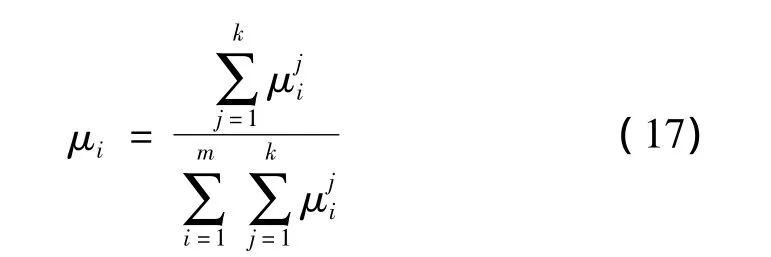
通過計算求得最優解的目標值為:f1=0.060 5;f2=0.072 2;f3=0.031
各個參數值為:m1=5;z1=32;b1=21.46;β1=6.186 7;i1=6.48;m2=10;z2=25;b2=32.52;β2=13.900 0。
3.3 優化結果比較分析
一般對離散變量的處理是先把變量當成連續變量進行求解,然后再對模數、齒數進行圓整處理。為了方便比較,本研究采用傳統方法進行求解,即先把離散變量當作連續變量求解,然后對求解結果進行標準化或者取整[11]。處理前的結果、處理后的結果以及本研究求解的結果如表1所示。
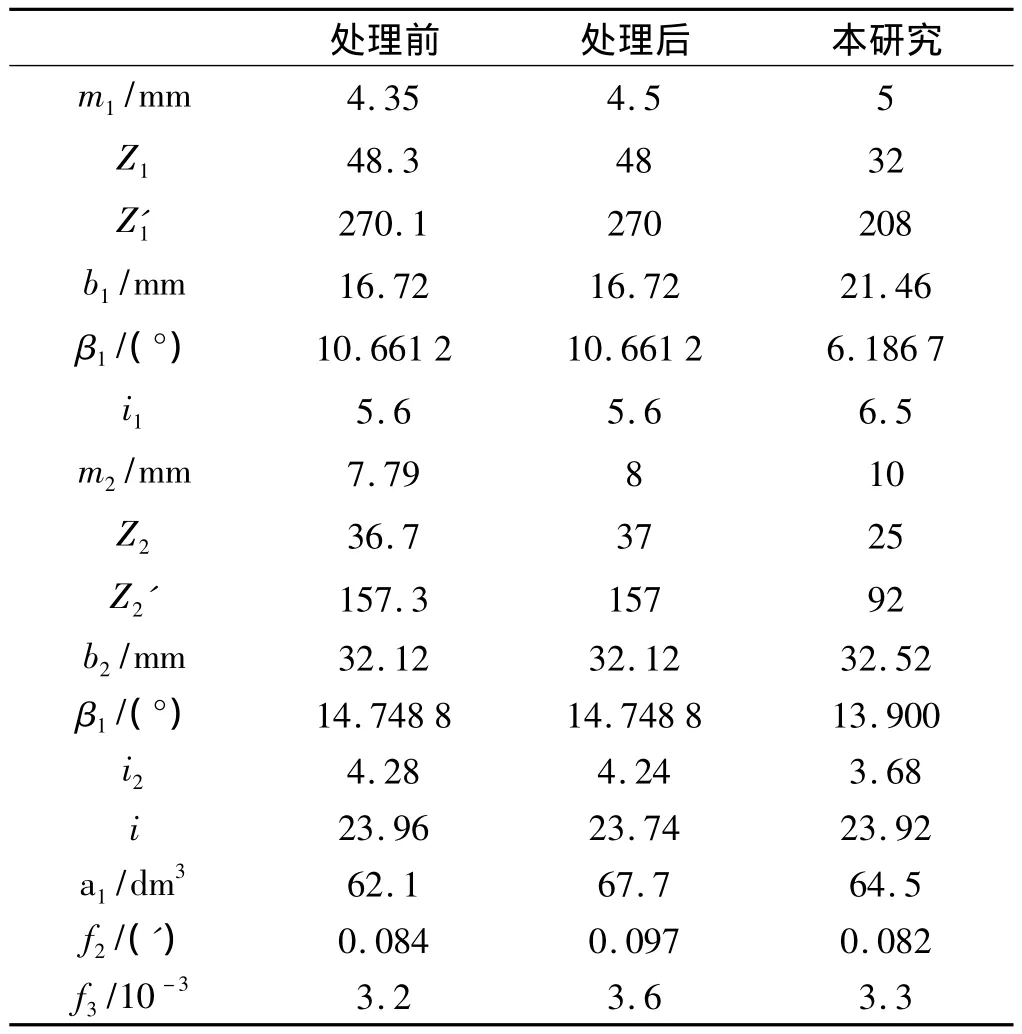
表1 優化結果比較
從表1中可以看出,采用傳統方法得到了很好的優化結果,但是模數不是標準值,齒數不是整數,并不能滿足工程需求,因此需要對模數取標準值,齒數取整數,然而經過處理之后,目標函數值都有不同程度的增加,優化效果有所降低。處理前、后對比,體積增加了9%;失效概率增加了15.5%;傳動誤差增加了12.5%,這是因為這些參數都是相互關聯的、相互制約的,人為地分成兩個步驟進行優化求解,難以保證優化結果最優。
本研究在非占優排序的時候就對離散變量進行處理,不符合要求的個體不會遺傳到下一代,保證了離散變量的值都是滿足要求的值。本研究方法求解的結果與傳統方法求解的結果相比,體積減少了4.7%;失效概率減少了15.5%;傳動誤差減少了8.3%。可以看出,優化結果更合理,而且減少了步驟,更有效率,更符合實際需求。因此,改進的非占優排序遺傳算法能夠很好地求解有離散變量、有約束的多目標優化問題。
4 結束語
針對有離散變量、多約束的多目標優化問題,本研究提出了離散變量和多約束的處理方法,并以減速器的優化設計為例,將優化結果與傳統方法的結果進行比較,來驗證該方法的有效性。
研究結果表明:該方法能很好地解決該類問題,有效地提升優化效果。
本研究采用的例子較為簡單,只有3個目標函數,9個變量,7個約束條件,然而有些優化問題復雜得多,有幾十甚至幾百個變量和約束條件,此時,運用該方法求解能否取得良好的結果還有待進一步的研究和驗證。
[1] 肖曉偉,肖 迪,林錦國,等.多目標優化問題的研究概述[J].計算機應用研究,2011,28(3):806-807.
[2] 寧曉斌,姜 健,謝偉東,等.基于汽車懸架的多目標優化方法的研究[J].機電工程,2011,28(2):166-168.
[3] ABIDO M A.Multi-objective evolutionary algorithms for electric power dispatch problem[J].IEEE Transactions on Evolutionary Computation,2006,10(3):315-329.
[4] 錢偉懿,李阿軍,楊寧寧.基于混沌的多目標粒子群優化算法[J].計算機工程與設計,2008,29(18):4794-4800.
[5] DEB K,PRATAP A,AGARWAL S.A fast and elitist multi-objective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):82-197.
[6] 王克喜.大規模定制下參數化產品族多目標智能優化方法與應用[D].長沙:湖南大學工商管理學院,2010:34-35.
[7] MITRA K,GOPINATH R.Multi-objective optimization of an industrial grinding operation using elitist nondominated sorting genetic algorithm[J].Chemical Engineering Science,2004,59(2):385-396.
[8] 陳國良,王煦法,莊鎮泉,等.遺傳算法及其應用[M].北京:人民郵電出版社,2001.
[9] RUI Li,TIAN Chang.Multi-objective optimization design of gear reducer base on adaptive genetic algorithm[J].IEEE Transactions on Systems,2008,6(1):229-234.
[10] 張 凱,蔣玲玲,劉夢迪.基于有限元法的減速器齒輪軸校核[J].輕工機械,2013,31(3):72-74.
[11] 高玉根,王國彪,丁予展.斜齒輪減速器遺傳算法的優化設計[J].起重運輸機械,2003,8(1):19.

