新的非線性彌散關系及其波浪變形數學模型

趙樹林，吳德安，諸裕良，邵宇陽

（河海大學 港口海岸與近海工程學院，南京 210098；河海大學 海岸災害及防護教育部重點實驗室，南京 210098）

新的非線性彌散關系及其波浪變形數學模型

趙樹林，吳德安，諸裕良，邵宇陽

（河海大學 港口海岸與近海工程學院，南京 210098；河海大學 海岸災害及防護教育部重點實驗室，南京 210098）

針對Hedges、Kirby、李瑞杰提出的修正非線性彌散關系在淺水區存在較大偏差的問題，給出了一個在整個水深范圍內相對波速具有單值性的新的非線性彌散關系。它在深水區與二階Stokes波的彌散關系相一致，在淺水區較前人的修正式與Hedges經驗彌散關系更加吻合，在中等水深區域與二階Stokes波的彌散關系及Hedges經驗彌散關系的偏差也達到最小。為了避免非線性彌散關系引入緩坡方程而導致的迭代，采用顯式形式近似表達該非線性彌散關系，得到與其精度幾乎完全相同的顯式表達式。用該顯式表達式，結合弱非線性效應的緩坡方程，得到考慮非線性彌散影響的波浪變形數學模型。用該模型對復雜地形進行模擬，計算結果與實測值吻合很好。

新的非線性彌散關系；顯式近似；波浪變形模型

Biography：ZHAO Shu?lin（1989-）,male,master student.

由于實際地形環境的復雜性及波浪的非線性影響，采用線性波動理論的波浪計算結果與試驗結果往往存在較大的誤差，尤其是在極淺水域，主要原因是在計算淺水波浪傳播時忽略了非線性影響。而波浪的非線性彌散關系可以在一定程度上反映波浪傳播的非線性效應，因此很多學者通過調整波浪的彌散關系來探討波浪傳播的非線性效應，提出了各種非線性彌散關系并進行了驗證，有效地解決了線性波動理論在實際應用中誤差較大的問題。

二階Stokes波的非線性彌散關系［1］只適用于深水和中等水深，不適用于淺水水域。Hedges［2］提出了一個適用于淺水的非線性經驗彌散關系，該經驗關系已被證明在淺水區精度很高［3-4］，但在深水區誤差較大。Kir?by和Dalrymple［5］構造了一個適用于任意水深的非線性彌散關系式，將二階Stokes波的彌散關系和Hedges的經驗彌散關系在中等水深處光滑銜接，但在中等水深處其相對波速出現最小值，與實際情況不符。為解決這一缺陷，Hedges［6］、Kirby和Dalrymple［7］分別給出了修正彌散關系，但在淺水區均與Hedges的經驗彌散關系存在較大偏差，且表達形式復雜。此后，李瑞杰等［8-9］先后又提出了新的非線性彌散關系，精度有所提高，然而當波陡較大時，在中淺水區與Hedges經驗彌散關系的偏差仍較大。

本文充分比較和分析了現有非線性彌散關系，給出了一個新的非線性彌散關系。它在深水區與二階Stokes波的彌散關系相一致，在淺水區與Hedges的經驗彌散關系很吻合，在中淺水深區域偏差也比前人結果小，波速隨相對水深的增大而單調減小，且形式簡單。考慮到非線性彌散關系結合含非線性效應的緩坡方程求解波浪變形問題時需要迭代運算，往往導致計算量太大，本文采用顯式形式來近似表達非線性彌散關系，得到的顯式表達式與新的非線性彌散關系非常吻合。最后，用新的非線性彌散關系的顯式表達式結合含弱非線性效應的緩坡方程，得到一個考慮非線性彌散影響的波浪變形模型。用該模型對復雜地形進行模擬，計算結果與實測值吻合很好。

1 非線性波浪彌散關系

只適用于深水和中等水深的二階Stokes波彌散關系［1］如下

式中：σ為角頻率；g為重力加速度；h為水深；k為波數，ε=ka，a為振幅，參數D=［cosh（4kh）+8-2tanh2（kh）］/［8sinh4（kh）］。

Hedges［2］通過對線性彌散關系進行調整，提出了一個適用于淺水的非線性彌散關系

許多研究［3-4,7］表明，式（2）在淺水區精度很高，但在中深水區誤差較大。

Kirby和Dalrymple［5］將式（1）和式（2）在中等水深處光滑銜接，構造了一個適用于任意水深的非線性彌散關系

式中：f1=tanh5（kh），f2=［kh/sinh（kh）］4。式（3）在深水逼近于式（1），在淺水逼近于式（2），因此使用式（3）的彌散關系比單獨使用式（1）或式（2）計算結果更為準確。

然而，在相對水深kh=1.5～2.5的中等水深區域，式（3）相對波速有隨相對水深增大而增大的趨勢，如圖2、圖3所示，這在實際中是不可能的。為此Hedges［6］提出了一個修正的非線性彌散關系

Kirby和Dalrymple［7］也提出了修正的非線性彌散關系

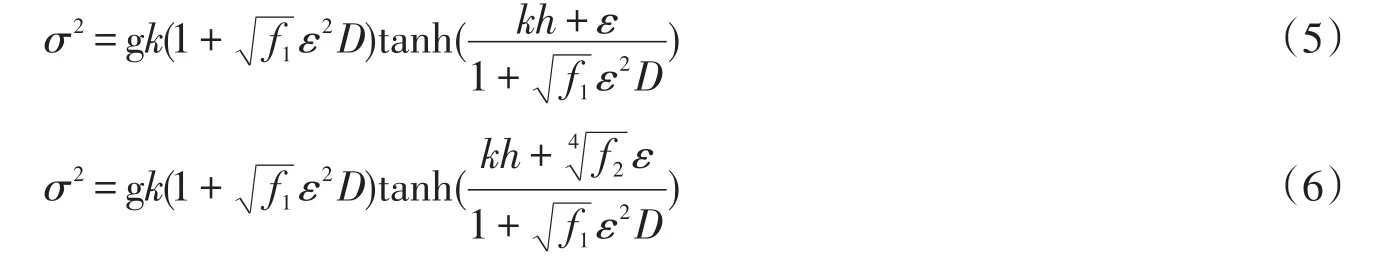
但是式（4）～式（6）的彌散關系在中淺水區都與式（2）存在較大的偏差，波陡較大時這種現象更加明顯，且其形式都過于復雜，不便于應用。

為此，李瑞杰等［8-11］又先后提出如下的非線性彌散關系

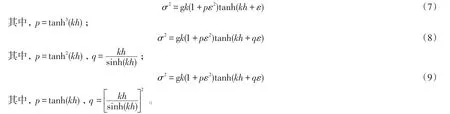
與前人結果相比，式（7）、（8）和（9）的彌散關系與式（1）或（2）彌散關系的偏差進一步縮小，其中以式（9）的彌散關系與式（1）和（2）最為逼近。然而當波陡較大時，式（9）在中淺水區與Hedges經驗彌散關系式（2）偏差仍較大。因此，本文根據tanh（kh）和kh/sinh（kh）的函數特性，分析了它們對非線性彌散關系的影響，并對前人彌散關系式進行了比較分析，建議采用下面的非線性彌散關系

式（10）和式（11）即為新的非線性彌散關系。用c代表非線性波速，c0代表深水波速，則有c/c0=σ2/（gk）。再用cl代表線性波波速，則cl/c0=tanh（kh）。因此，可以用（c-cl）/c0考察以上各式的非線性影響，并對它們的精度進行比較。

圖1給出了不同的波陡時新的彌散關系式（10）與二階 Stokes波的彌散關系式（1）及Hedges的經驗彌散關系式（2）的比較。可以看出對于不同的波陡，式（10）在淺水區與式（2）相一致，在深水區與式（1）相一致。在中等水深區域式（10）將式（1）和式（2）平滑銜接，相對波速沒有出現最小值的現象。尤其當波陡較小（ε=0.1）時，式（10）與式（1）、（2）更加逼近，精度很高。

圖2、圖3分別給出了ε=0.2和ε=0.3時各種非線性彌散關系隨相對水深變化的比較。可以看出，Kirby的彌散關系式（3）在相對水深kh=1.5～2.5的中等水深區域，相對波速有隨相對水深增大而增大的趨勢，與實際情況不符。Hedges 的修正彌散關系式（4）在中等水深區域與二階Stokes波的彌散關系式（1）及Hedges經驗彌散關系式（2）偏差較大。Kirby的修正彌散關系式（6）在相對水深kh＜1的淺水區域，與式（2）偏差較大。李瑞杰的彌散關系式（9）在波陡較小（ε=0.2）時精度較高，而當波陡較大（ε=0.3）時，在相對水深kh＜1的淺水區域，與式（2）的偏差仍較大。當波陡較小時，本文的彌散關系式（10）與式（9）精度相當，較前人結果與式（1）及式（2）的偏差達到最小；而當波陡較大時，本文的彌散關系式（10）在淺水區域比式（9）更逼近于Hedges經驗彌散關系式（2）。

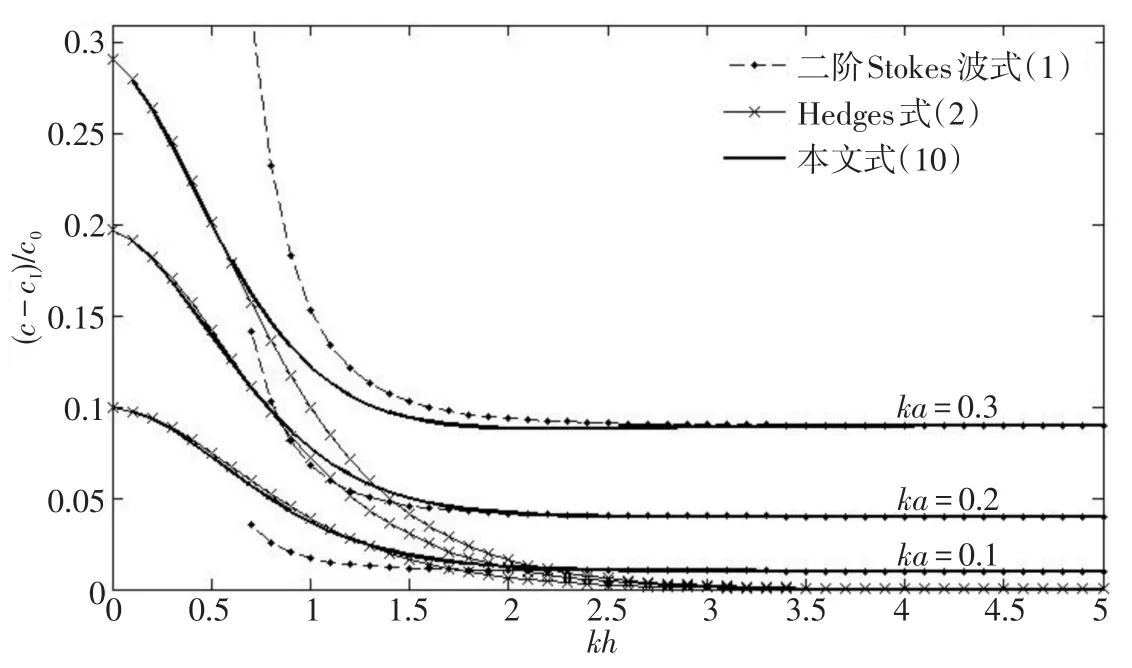
圖1 新的彌散關系與式（1）及式（2）彌散關系比較Fig.1Comparison of the new dispersion relation with Eq.（1）and Eq.（2）

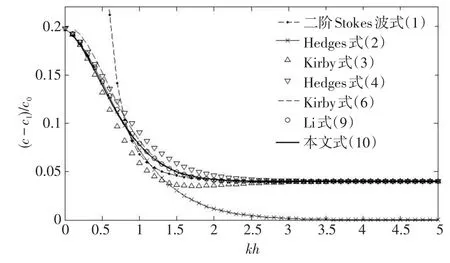
圖2 各種非線性彌散關系隨相對水深變化的比較（ε=0.2）Fig.2 Comparison of various nonlinear dispersion relations at ε=0.2

2 非線性彌散關系的顯式近似

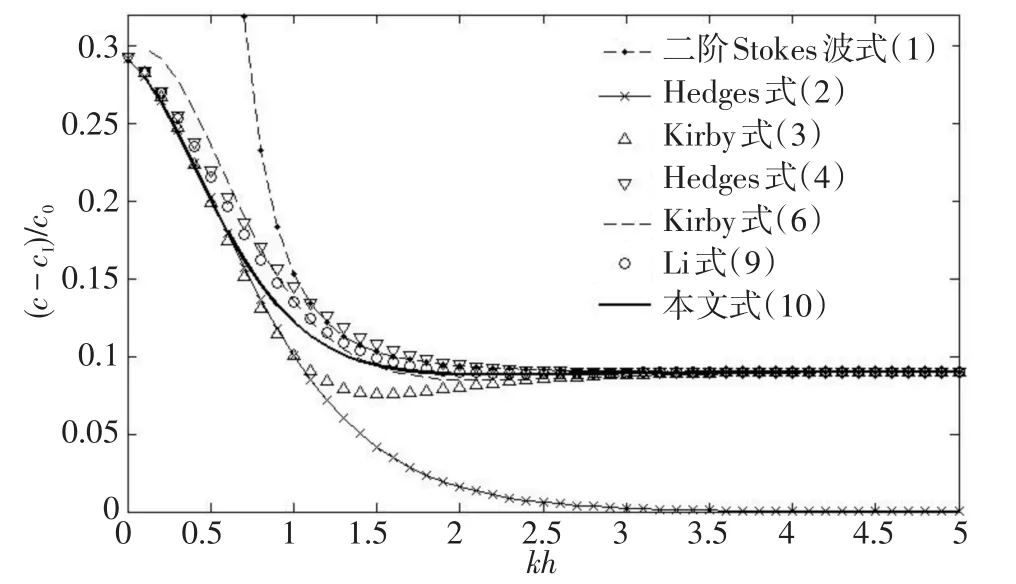
圖3 各種非線性彌散關系隨相對水深變化的比較（ε=0.3）Fig.3 Comparison of various nonlinear dispersion relations at ε=0.3

為了避免在緩坡方程中由于非線性彌散關系的引入而導致的迭代，將新的非線性彌散關系式（10）在ε=0處關于ε做Taylor級數展開，略去4階以上小量，可寫成下面的顯式表達式

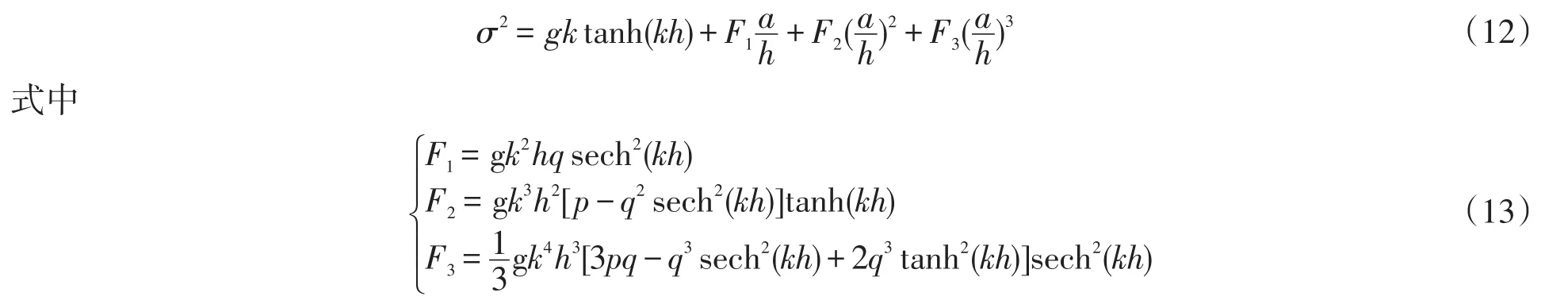
式（12）和式（13）即為新的非線性彌散關系式（10）的顯式表達式。圖4為不同的波陡時顯式近似式（12）與式（10）的比較，可以看出式（12）的顯式表達式與式（10）非常吻合。

3 考慮非線性彌散影響的波浪變形模型

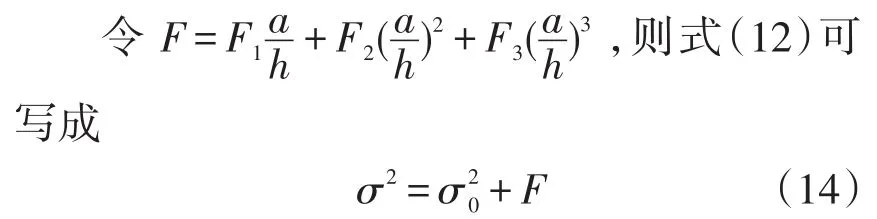
式中：=gktanh（kh）為線性彌散關系。再根據含非線性項的緩坡方程可得［12-15］

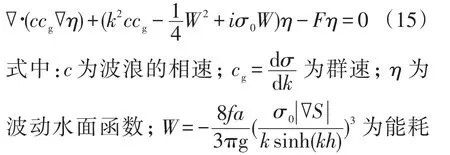
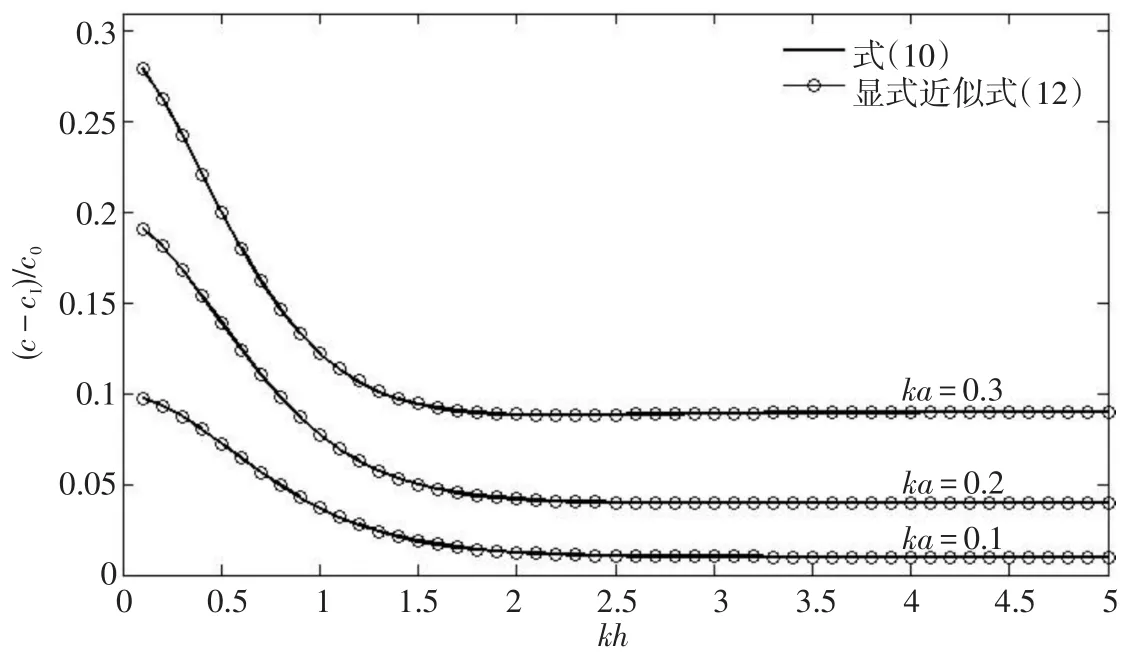
圖4 不同的波陡時顯式近似式與式（10）的比較Fig.4 Comparison of explicit approximation with the new dispersion relation

采用前進波假設，令η=a（x,y）eiS（x,y），代入式（15）分離實部和虛部分別得

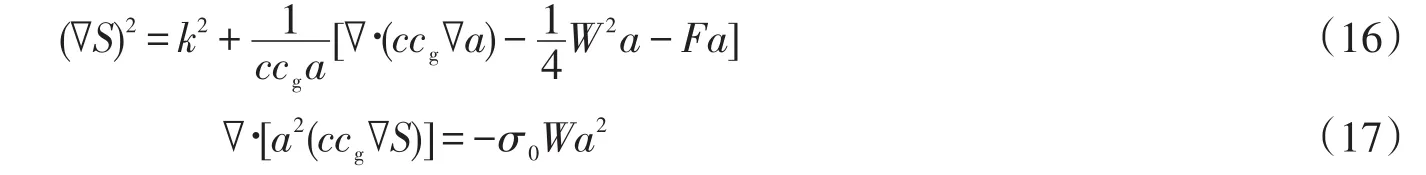
由波浪位相函數梯度的無旋性?×（?S）=0得

式中：θ為波向角。式（16）～式（18）構成一個考慮非線性彌散影響的波浪變形數學模型。若令式（16）中F=0，則忽略非線性彌散影響，相應地構成線性波浪變形數學模型。

4 模型應用及結果分析

采用Yoo&O′Connor雙橢圓試驗［16］對文中的波浪變形數學模型進行驗證。試驗地形及測量斷面布置如圖5，斜坡坡度為1：50，斜坡梯度方向與x軸夾角為20°。波浪沿x軸正方向入射，振幅a0=0.024 5 m，周期T0=1.0 s。

圖6給出了斷面1～8相對振幅數模計算值與實測值的對比。斷面1～5較清晰地反映了波浪傳播經過兩個淺灘后分別出現波高增大的現象，線性解相對振幅波動幅度比實測值偏大，反映了線性數學模型對于復雜地形的變化較為敏感；而非線性解相對振幅波動幅度與實測值較為一致。斷面6在18＜x＜24的區域線性數學模型計算結果與實測值差異較大，而非線性數學模型計算結果與實測值吻合的較好。斷面8無論是線性模型還是非線性模型的計算結果都出現了較大的偏差，原因可能是波浪經橢圓淺灘后產生了駐波，具體的原因和解決方法還有待進一步研究。

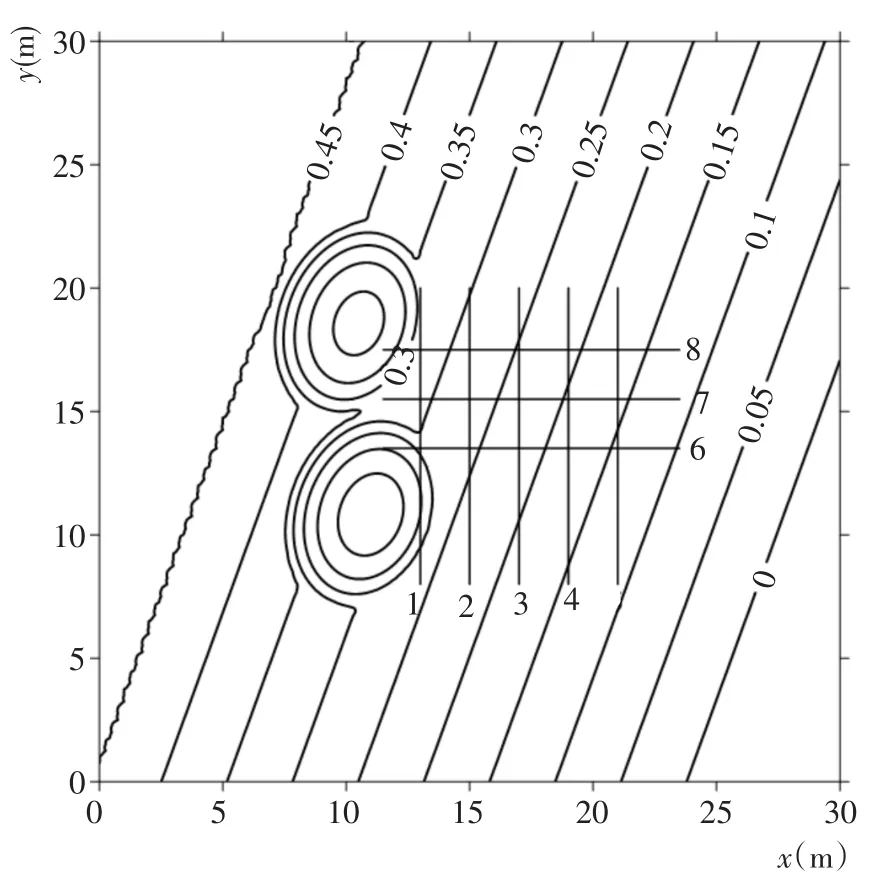
圖5 實驗地形及測量斷面布置Fig.5 Laboratory topography and gauge section layout

總體而言，非線性模型的計算結果要優于線性模型的計算結果，具有較好地擬合精度。由此可見，非線性影響在復雜地形的波浪變形中是不能忽略的，考慮波浪的非線性影響可以得出與試驗數據更為相符的結果。

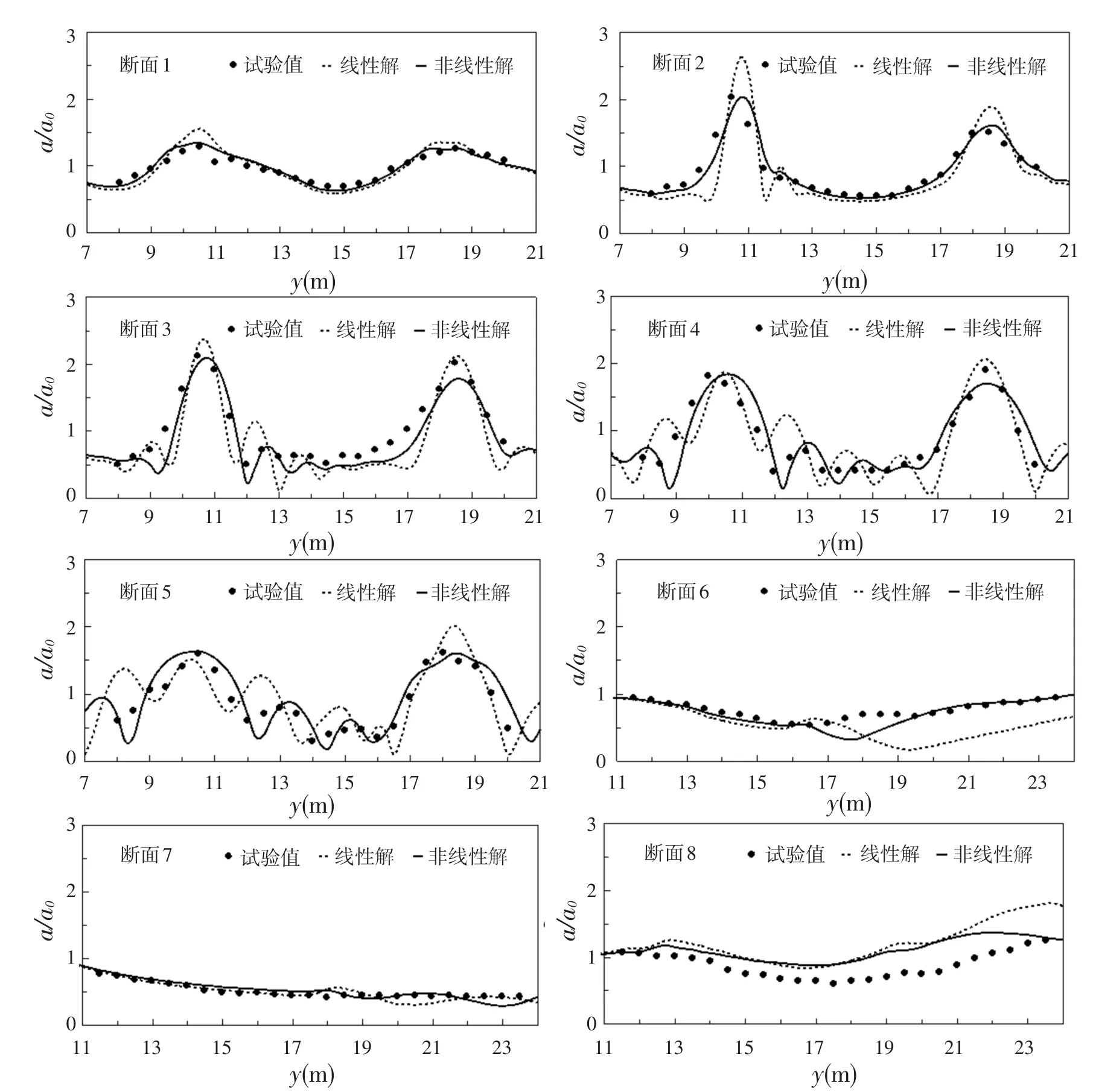
圖6 斷面1～8相對振幅計算值與實測值對比Fig.6 Comparison of computing relative wave amplitudes with measured data at section 1～8

5 結語

文中給出一個新的非線性彌散關系，它在深水區與二階Stokes波的彌散關系相一致，在淺水區與Hedges經驗彌散關系相吻合，在中等水深處光滑銜接，相對波速在整個水深范圍內具有單值性。與前人的修正式相比，當波陡較大時，本文的非線性彌散關系在淺水區與Hedges經驗彌散關系更加吻合；而當波陡較小時，本文的非線性彌散關系與李瑞杰（2004年）的彌散關系精度相當，在中等水深區域與二階Stokes波的彌散關系及Hedges經驗彌散關系的偏差達到最小。

采用顯式形式近似表達新的非線性彌散關系，得到了與該非線性彌散關系精度幾乎完全相同的顯示表達式。再用該顯式表達式結合弱非線性效應的緩坡方程，得到考慮非線性彌散影響的波浪變形數學模型。采用Yoo&O′Connor雙橢圓試驗對該模型進行驗證，計算結果和實測值吻合很好，表明新的非線性彌散關系得到的波浪變形數學模型對復雜地形具有較高的模擬精度。

［1］Whitham G B.Non?linear dispersion of water waves［J］.Fluid Meeh.,1967,27（2）：399-412.

［2］Hedges T S.An empirical modification to linear wave theory［J］.Proc.Inst.Civ.Eng，1976,61：575-579.

［3］Booij N.Gravity waves on water with non?uniform depth and current［R］.Dept.Civ.Eng：Delft University of Technology,1981.

［4］ Dingemans M W.Water wave propagation over uneven bottoms［M］.Singapore：World Scientific,1997.

［5］Kirby J T,Dalrymple R A.An approximate model for nonlinear dispersion in monochromatic wave propagation models［J］.Coast?al Eng.,1986（9）：545-561.

［6］Hedges T S.An approximate model for nonlinear dispersion in monochramatic wave propagation models［J］.Coastal Eng.,1987（13）：23-54.

［7］Kirby J T,Dalrymple R A.An approximate model for nonlinear dispersion in monochramatic wave propagation models［J］.Coast?al Eng.,1987（11）：89-92.

［8］李瑞杰,LEE D Y,諸裕良.非線性彌散效應及其對波浪變形的影響［J］.海洋工程,2001,19（4）：46-51.

LI R J,LEE D Y,ZHU Y L.Nonlinear dispersion effect on wave transformation［J］.The Ocean Engineering,2001,19（4）：46-51.

［9］Li Ruijie,Dong?Young Lee.Nonlinear dispersion effect on wave transformation［J］.China Ocean Engineering,2000,14（3）：375-384.

［10］Li Ruijie,Yan Yi xin,Cao Hongsheng.Nonlinear dispersion relation in wave transformation［J］.China Ocean Engineering,2003,17（1）：117-122.

［11］李瑞杰,張揚,曹宏生.波浪非線性彌散關系及其應用［J］.海洋工程,2004,22（11）：20-24.

［12］洪廣文,馮衛兵，張洪生，等.海岸河口水域波浪傳播數值模擬［J］.河海大學學報,1999（2）：1-9.

HONG G W,FENG W B,ZHANG H S,et al.Numerical Modelling of Wave Propagation in Water of Varying Topography and Cur?rent［J］.Journal of Hohai University,1999（2）：1-9.

［13］KIRBYJT,DALRYMPLERA.Verification of parabolic equation for propagation of weakly of nonlinear waves［J］.Coastal Engineer?ing,1984（8）：219-232.

［14］Li Rujie,Wang Houjie.A modified from of mild slope equation with weakly nonlinear effect［J］.China Ocean Engineering,1999,13（3）：327-333.

［15］李瑞杰,王爰群,王厚杰.波浪在淺水傳播中的弱非線性效應［J］.海洋工程,2000,18（3）：30-33.

［16］Yoo D,OcConnor B A.Diffraction of waves in caustics［J］.J.Wtrwy.,Port,Coast and Oc.Engrg.ASCE,1988,114（6）：731-751.

Nonlinear dispersion relation and wave transformation model

ZHAO Shu?lin,WU De?an,ZHU Yu?liang,SHAO Yu?yang
（College of Harbor,Coastal and Offshore Engineering,Hohai University,Nanjing210098,China;Key Laboratory of Coastal Disaster and Defence,Ministry of Education,Hohai University,Nanjing210098,China）

Due to the larger deviation in shallow water of the nonlinear dispersion relations modified by Hedg?es,Kirby and Li Ruijie,a new nonlinear dispersion relation,whose relative wave velocity was monotonic in the en?tire depth,was presented in this paper.It is consistent with the dispersion relation of second order stokes wave in deep water,and is closer to Hedges′empirical one than previous modified relations in shallow water.In moderate depth water,its deviation is also minimal.In order to avoid iterations due to the introduction of nonlinear dispersion relation to the mild slope equation,an explicit form was adopted to approximately express the new nonlinear disper?sion relation.And the accuracy of the two was almost identical.The explicit expression,along with the mild slope equation,could constitute a wave transformation model,which included nonlinear dispersion effects.Using the new model to simulate a complicated seabed,the calculation results are in good agreement with the measured values.

new nonlinear dispersion relation;explicit approximation;wave transformation model

TV 139.2+5

A

1005-8443（2014）03-0203-06

2013-08-06；

2013-10-14

趙樹林（1989-），男，山東省煙臺人，碩士研究生，主要從事河口海岸動力學研究。