基于BP神經網絡的粒子濾波算法

王爾申，李興凱，龐濤（沈陽航空航天大學電子信息工程學院，遼寧沈陽110136）

基于BP神經網絡的粒子濾波算法

王爾申，李興凱，龐濤
（沈陽航空航天大學電子信息工程學院，遼寧沈陽110136）

針對粒子濾波算法中的粒子退化問題，提出了一種基于BP神經網絡的提高粒子濾波多樣性的算法。利用BP神經網絡的非線性映射功能，通過對權值進行分裂、選擇，將粒子中的小權值粒子狀態作為神經網絡的輸入，粒子的權值作為神經網絡的權值，以觀測值作為神經網絡的目標信號，通過多次訓練增大小權值粒子的權值，從而提高粒子濾波算法粒子的多樣性，改善算法的濾波性能。仿真結果表明：基于BP神經網絡的粒子濾波算法的性能在有效粒子數和均方根誤差參數方面優于基本粒子濾波算法，在改善濾波精度方面得到了較好的效果，驗證了BP神經網絡在改進粒子濾波算法中的有效性。

粒子濾波；粒子退化；重采樣；BP神經網絡

粒子濾波（particle filter，PF）算法是一種基于蒙特卡羅模擬和遞推貝葉斯估計的濾波方法，隨著采樣粒子數的增大，逐漸趨向狀態的后驗概率密度，在處理非高斯、非線性系統的參數估計和狀態濾波問題方面有著明顯的優勢。近年來，在目標跟蹤、衛星姿態估計、金融領域數據分析、圖像處理、衛星導航動態定位等方面得到廣泛的應用［1?5］。對于粒子濾波而言，其主要的缺陷是存在粒子退化現象。采用重采樣技術能抑制粒子退化現象，但同時也帶來了粒子的多樣性喪失、樣本枯竭等問題。

文獻［6］將卡爾曼濾波與粒子濾波結合提高估計精度。文獻［7］將粒子濾波與神經網絡結合，可克服神經網絡算法易陷于局部極小的缺陷。文獻［8］將粒子濾波與自組織模糊神經網絡訓練算法相結合，利用粒子濾波對參數進行學習，其在結構緊湊性和泛化性能上有所提高。上述這些算法是將粒子濾波用于神經網絡算法的改善。

1 基本粒子濾波算法

Gordon提出基于蒙特卡羅方法的序貫重要性重采樣粒子濾波算法以來，粒子濾波成為非線性非高斯系統狀態估計問題的一個研究熱點［9］。

假設描述動態系統的狀態方程和觀測方程為

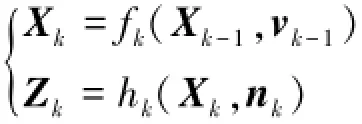
式中：Xk為狀態向量，Zk為測量向量，fk為狀態轉移函數，hk為狀態向量和觀測向量之間的傳遞函數，vk－1為系統噪聲，nk為觀測噪聲。基本粒子濾波算法的步驟如下所示。

設k－1時刻有一組后驗粒子集：

｛xk－1（i），ωk－1（i）；i＝1，2，…，N｝

式中：N為粒子數目，xk－1（i）為k－1時刻的第i個粒子，ωk－1（i）為k－1時刻第i個粒子的權重。

1）粒子集初始化，k＝0。

根據先驗概率密度p（X0）抽取隨機樣本，X0

（1），X0

（2），…，（N為隨機樣本數）。

2）當k＝1，2，…時，執行以下步驟：

①狀態預測。根據系統的狀態方程抽取k時刻的先驗粒子：

｛Xk｜k－1（i）；i＝1，2，…，N｝～p（Xk｜Xk－1）

②更新。首先，進行權值更新。在獲得測量值之后，根據系統的觀測方程計算粒子的權值：

③估計。計算當前時刻系統的狀態估計值：

基本粒子濾波算法在k時刻抽樣時保持了過去的樣本不變，而且重要性權是迭代計算的。但重要性權的方差經過若干次迭代，某個權可能趨于1，其余的權趨于0，造成了權值退化現象。粒子濾波的重采樣可以抑制權值的退化，但重采樣后也帶來粒子不再獨立。

2 BP神經網絡輔助的粒子濾波算法

BP神經網絡是一種有教師信號的按誤差逆傳播算法訓練的多層前饋網絡。它的學習規則使用最速下降法，通過反向傳播來不斷調整網絡的權值和閾值，使網絡的誤差平方和最小。BP神經網絡模型拓撲結構包括輸入層、隱層和輸出層，如圖1所示。

圖1 BP神經網絡結構示意圖Fig.1 Diagram of BP neural network

設輸入樣本為p個：x1，x2，…，xp，與之對應的教師信號為d1，d2，..，dp，實際輸出為y1，y2，…，yp，輸出誤差為

采用梯度法對各個層之間的權值進行調整，以使總誤差減小，即

式中：η為學習步長，wjk為各層之間的權值，Δwjk為權值修改量，通過總誤差對權值進行相應地調整。

將BP神經網絡與粒子濾波算法結合，改進的粒子濾波在基本粒子濾波的基礎上增加了權值分裂和權值調整2個步驟，BP神經網絡輔助的重要性權值調整粒子濾波（NNWA?PF）算法詳細步驟如下。

1）粒子集初始化，k＝0。

根據先驗概率密度p（X0）產生隨機樣本，X0

（1），，…，（N為隨機樣本數）。

2）當k＝1，2，…時，執行以下步驟：

①狀態預測。根據系統的狀態方程抽取k時刻的先驗粒子：

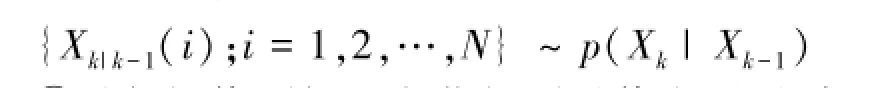
②進行權值更新。在獲得測量值之后，根據系統的觀測方程并計算粒子的權值：

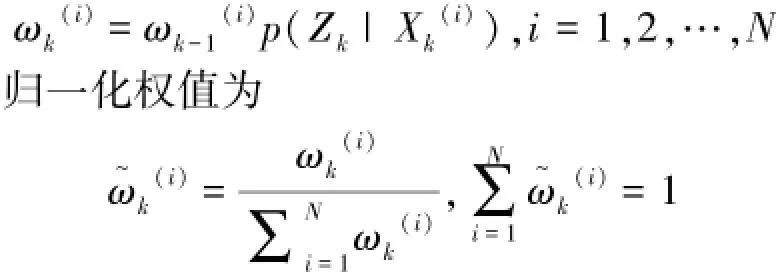
③粒子分裂。將粒子矩陣按權值大小排序，分為高權值矩陣和低權值矩陣，將高權值矩陣中q個權值大的粒子分裂為2個小的、權值減半的粒子，同時將低權值矩陣中的q個權值最小的粒子舍棄。

④權值調整。將③的粒子權值矩陣進行降序排列，取其中最小的q個粒子，利用BP神經網絡調整粒子的權值。

設誤差能量定義為

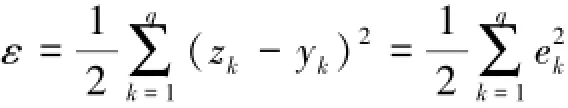
式中：q為輸入／輸出層神經元的數量，zk為教師信號，即系統在該時刻的量測值，yk為神經網絡的輸出。輸入數據為具有較小權值的粒子，其狀態值作為BP神經網絡的輸入，粒子權值作為神經網絡的初始權值，樣本的學習函數為系統量測方程。

對更新后的粒子的權值進行歸一化，

⑥估計。計算當前時刻系統的狀態估計值：

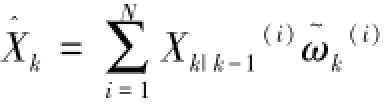
⑦時刻k＝k＋1，繼續計算。

3 實驗仿真與結果分析

3.1 實驗模型

為了進一步驗證算法的有效性，本文引用如下的模型［10］，該模型在大量文獻中均可看到，是研究比較各種粒子濾波算法性能的典型驗證模型之一。

狀態模型和觀測模型分別為

式中：k表示狀態時刻，xk表示狀態量，yk表示觀測量，狀態初始值為x0＝0.1，wk、vk均服從零均值高斯分布，方差分別為和，狀態變量xk為一維變量，初始狀態x0服從高斯分布。

3.2 實驗結果性能分析

依據上述模型中的系統方程與測量方程，設定初始時刻狀態值x0和粒子總數，神經網絡的學習步長為0.05，神經元個數為6，過程噪聲方差Q＝1、量測噪聲方差R＝1時。運行環境為MATLAB R2009a，Intel Core（TM）2 Duo CPU T6500，2.1 GHz，2 G內存。為了對比不同粒子數目的實驗結果，選取50、100、150個粒子，結果如圖2～7所示。

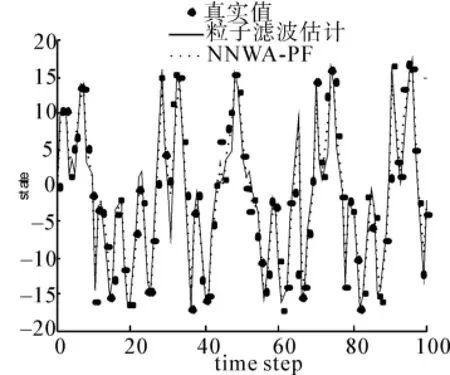
圖2 粒子數為50時算法結果對比情況Fig.2 Com parison of the algorithms un?der the condition of 50 particles

圖3 粒子數為50時誤差對比情況Fig.3 Error comparison under the condition of 50 particles

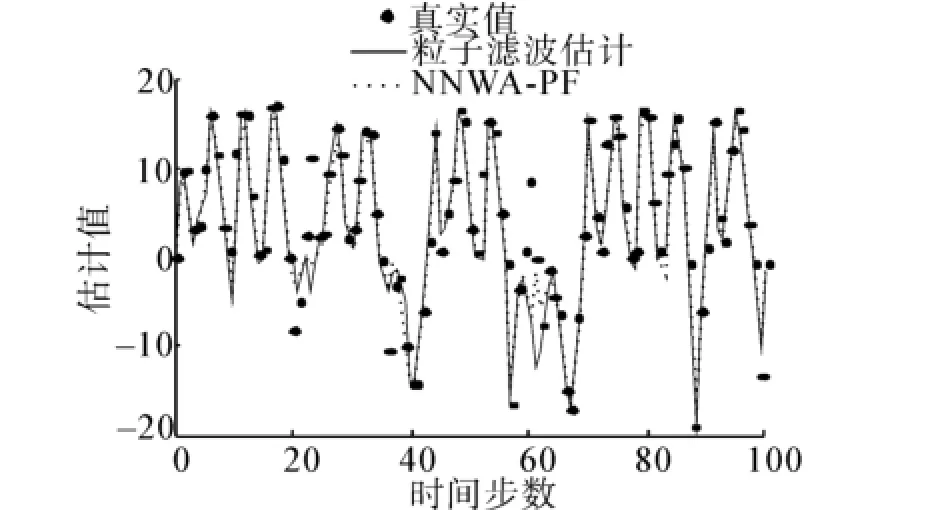
圖4 粒子數為100時算法結果對比情況Fig.4 Com parison of the algorithm s under the condi?tion of 100 particles

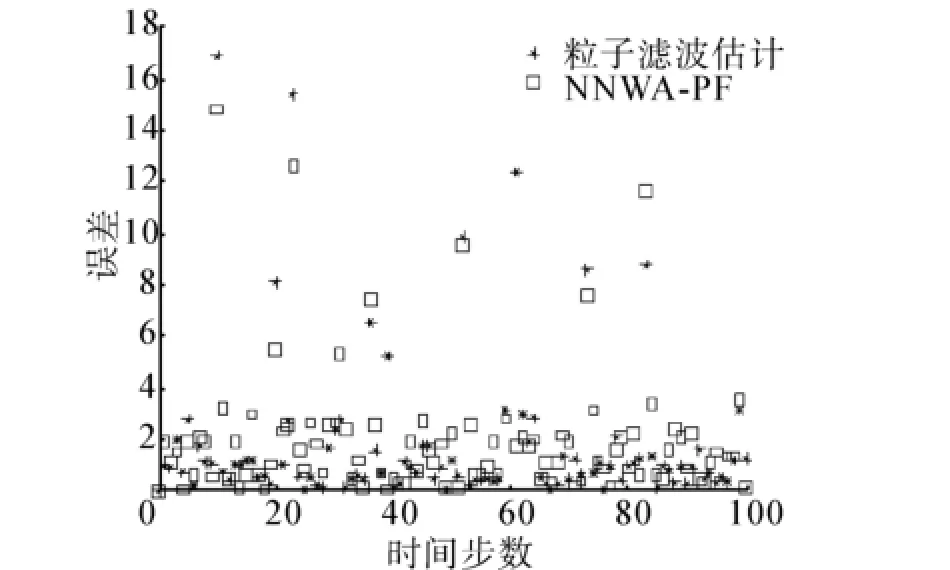
圖5 粒子數為100時誤差對比情況Fig.5 Error comparison under the condition of 100 particles

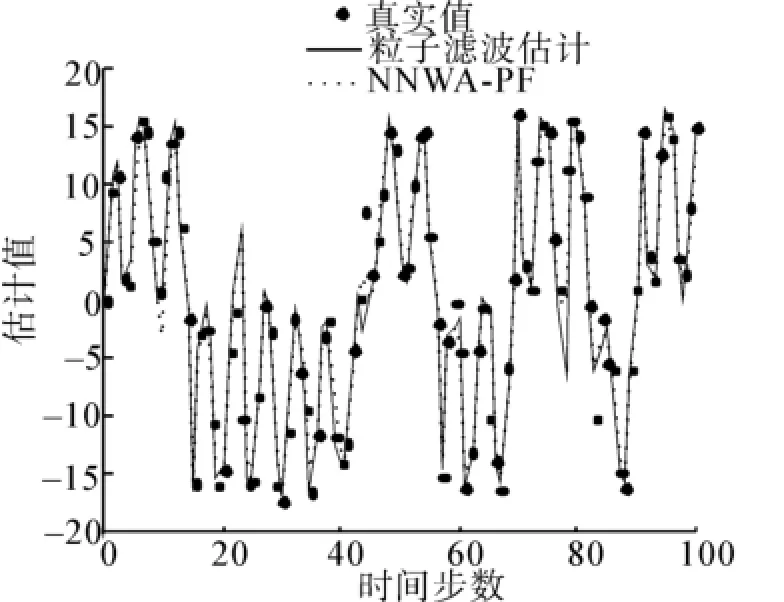
圖6 粒子數為150時算法結果對比情況Fig.6 Com parison of the algorithm s under the condition of 150 particles

圖7 粒子數為150時誤差對比情況Fig.7 Error com parison under the condition of 150 particles

從圖中可以看出，BP神經網絡輔助的粒子濾波算法比基本粒子濾波算法對狀態的估計性能更好。2種算法處理后的不同參數如表1所示。

從表1不難看出，粒子數目為N＝50，NNWA?PF濾波算法的RMSE＝3.539 9，基本粒子濾波算法的RMSE＝3.816 3。此時，NNWA?PF濾波算法的有效樣本為30.415 5。粒子數目為N＝100時，NNWA? PF濾波算法的RMSE＝3.175，基本粒子濾波算法的RMSE＝3.517 8。此時，NNWA?PF濾波算法的有效樣本為48.1209。粒子數目為N＝150時，NNWA?PF濾波算法的RMSE＝3.111 8。此時，NNWA?PF濾波的有效樣本為71.265 0。從中可以看出引入神經網絡后的重要性權值調整粒子濾波算法能有效地抑制樣本退化，而且，在同等條件下，有效樣本數目增多，方差越小，估計精度越高。

表1 采用不同算法處理后的參數比較Table 1 Parameter comparison of particle filter algorithms

為了驗證不同算法復雜度與粒子濾波中粒子個數N的關系，分別選取50，100，…，350個粒子，仿真其運行時間（單位：s），得到的結果如圖8、9所示。

圖8 粒子濾波算法運行時間與粒子數目的關系Fig.8 Relation of PF running time and number of par?ticle

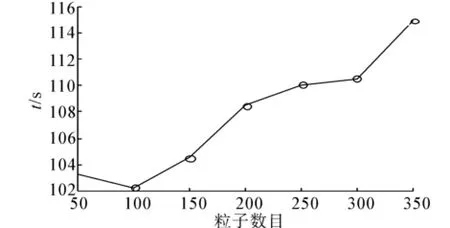
圖9 NNWA?PF算法運行時間與粒子數目的關系Fig.9 Relation of NNWA?PF running time and num?ber of particle

從圖8和圖9中可看出，基本粒子濾波算法的運行時間隨著粒子數目的增加基本成線性增長。NNWA?PF的運行時間隨著粒子數目的增加成非線性增長。

4 結束語

將BP神經網絡和基本粒子濾波算法有機結合，通過理論分析和數學仿真，比較了相同粒子數樣本條件下，BP神經網絡輔助的粒子濾波與基本粒子濾波的有效粒子數目和均方根誤差參數，分析了不同粒子數目條件下算法的復雜度。結果表明：神經網絡輔助的粒子濾波算法有效地改善了濾波性能，降低了估計方差，同時，粒子濾波器運行時間均與粒子數目呈遞增關系，BP算法的引入增加了算法的運行時間。

［1］程水英，張劍云.粒子濾波評述［J］.宇航學報，2008，29（4）：1099?1111.CHENG Shuiying，ZHANG Jianyun.Review on particle fil?ters［J］.Journal of Astronautics，2008，29（4）：1099?1111.

［2］LI P，KADIRKAMANATHAN V.Particle filtering based likelihood ratio approach to fault diagnosis in nonlinear sto?chastic systems［J］.IEEE Trans Syst，Man，Cybern C，2001，31（3）：337?343.

［3］GUSTAFSSON F，FREDRIK G.Particle filters for positio?ning，navigation，and tracking［J］.IEEE Transactions on Signal Processing，2002，50（2）：425?437.

［4］QINGMing，JO K H.A novel particle filter implementation for a multiple?vehicle detection and tracking system using tail light segmentation［J］.International Journal of Control，Automation and Systems，2013，11（3）：577?585.

［5］CHEN Zhimin，BO Yuming，WU Panlong，etal.Novelpar?ticle filter algorithm based on adaptive particle swarm opti?mization and its application to radar target tracking［J］.Control and Decision，2013，28（2）：193?200.

［6］夏楠，邱天爽，李景春，等.一種卡爾曼濾波與粒子濾波相結合的非線性濾波算法［J］.電子學報，2013，41（1）：148?152.XIA Nan，QIU Tianshuang，LIJingchun，et al.A nonlinear filtering algorithm combining the kalman filter and the parti?cle filter［J］.Acta Electronica Sinica，2013，41（1）：148?152.

［7］陳養平，王來雄，黃士坦.基于粒子濾波的神經網絡學習算法［J］.武漢大學學報：工學版，2006，39（6）：86?88.CHEN Yangping，WANG Laixiong，HUANG Shitan.Neural network learning algorithm based on particle filter［J］.Engi?neering Journal ofWuhan University，2006，39（6）：86?88.

［8］程洪炳，黃國榮，倪世宏，等.基于粒子濾波的自組織模糊神經網絡算法研究［J］.儀器儀表學報，2011，32（3）：634?639.CHENG Hongbing，HUANG Guorong，NI Shihong，et al.Desighn of self?organizing fuzzy neural network based on particle filter［J］.Chinese Journal of Scientific Instrument，2011，32（3）：634?639.

［9］ARULAMPALAM M S，MASKELL S，GORDON N，et al.A tutorial on particle filters for online nonlinear／non?Gaussi?an Bayesian tracking［J］.IEEE Transactions on Signal Pro?cessing，2002，50（2）：174?188.

［10］馮馳，趙娜.有效粒子數MCMC粒子濾波算法研究［J］.應用科技，2009，36（4）：19?22.FENG Chi，ZHAO Na.Research on MCMC particle filter algorithm［J］.Applied Science and Technology，2009，36（4）：19?22.

王爾申，男，1980年生，副教授，博士，主要研究方向為衛星導航信號處理算法以及航空電子系統。主持多項縱向項目，發表學術論文20余篇。

李興凱，男，1988年生，碩士研究生，主要研究方向為衛星導航信息處理。

龐濤，女，1976年生，講師，主要研究方向為機器人學、人工智能，發表學術論文10篇。

A particle filtering algorithm based on the BP neural network

WANG Ershen，LIXingkai，PANG Tao
（School of Electronic and Information Engineering，Shenyang Aerospace University，Shenyang 110136，China）

Aiming at the particle degeneracy phenomena in particle filtering algorithms，a particle filtering algorithm based on the BP neural network is presented for improving the diversity of particles.This algorithm utilizes the non?linearmapping function of the BP neuralnetwork.Firstof all，to sample particles from the importance density func?tion of particleweight division，theweighted particle is split into two smallweight particles.Next，theweightof ver?y small particles is abandoned and the particleswith smallerweightare adjusted using the neural network.The state of the remaining smallweight particles is used as the inputof neural network.The weights of particles are treated as the weights of neural network by using the observed value as the target signal of the neural network.The weights of many small particles can be increased through many times′trainings，thereby increasing the diversity of particle samples in the particle filter algorithm.Simulation results showed that the particle filter algorithm based on BP neu?ral network can increase the number of effective particles，reduce themean square error，and the filtering precision performance is improved.It is proven that this particle filter algorithm based on BP neural network is reliable and effective.

particle filter；particle degeneracy；resampling；BP neural network

TP391

A

1673?4785（2014）06?0709?05

王爾申，李興凱，龐濤.基于BP神經網絡的粒子濾波算法［J］.智能系統學報，2014，9（6）：709?713.

英文引用格式：WANG Ershen，LIXingkai，PANG Tao.A particle filtering algorithm based on the BP neural network［J］.CAAI Transactions on Intelligent Systems，2014，9（6）：709?713.

10.3969／j.issn.1673?4785.201310057

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1673?4785.201310057.htm l

2013?10?22.

日期：2014?09?30.

國家自然科學基金資助項目（61101161）；航空科學基金資助項目（2011ZC54010）；遼寧省自然科學基金（聯合基金）資助項目（2013024003）.

王爾申.E?mail：wes2016＠sau.edu.cn.