牽制控制下復雜網絡的同步性研究

仇建平，陳立潮，潘理虎（太原科技大學計算機科學與技術學院，山西太原030024）

牽制控制下復雜網絡的同步性研究

仇建平，陳立潮，潘理虎
（太原科技大學計算機科學與技術學院，山西太原030024）

復雜網絡是由數量巨大的節點組成，任何人都無法控制所有節點.只有通過控制少數節點，對復雜網絡進行牽制控制，才能達到網絡同步的目的.為此分析了一般網絡和含有生成樹的網絡同步的條件，給出了實現算法及運行界面.仿真結果表明，隨著網絡規模的擴大，驅動節點的比例減小，驅動節點常常都是入度低的節點.

復雜網絡；耦合；牽制；生成樹；同步

社會系統本質上是一個復雜系統，特別是隨著現代社會的飛速發展，對資源的需求也越來越大。單項資源已無法支撐整個社會的全面發展，且只有各單項資源互相耦合、互相牽制，才能形成強大的支撐合力。一旦某種或幾種資源缺失或失效，社會系統的內在結構及功能會遭到極大的破壞。例如，2003年9月28日發生在意大利的大面積停電事件，最初由于一個供電站的失效致使眾多供電站與整個供電網的脫離，隨后又致使眾多Internet網絡節點失效，最終致使整個電力調度系統無法調控，導致了更大規模的停電［1?2］。

隨著通信網、電力網、交通網、供水網等復雜動態網絡的發展，以及大型高速計算機、巨型數據庫以及GPS和基于大數據的社會計算的普及，復雜動態網絡特別是多節點不規則連接的有向網絡的牽制控制越來越受到關注。如劉彧［3］研究了復雜動態網絡節點從任意初態控制到任意終態的完全能控性問題；王文旭［4］提出了一種減少控制節點的方法；Ne?pusz［5］研究了運用點邊互換的思想對網絡的邊的狀態進行控制的問題；嚴鋼［6］研究了控制復雜網絡的能量代價問題。

1 網絡模型

1.1 模型示例

一個復雜動態網絡是具有相互耦合和牽制關系的點或網絡所組成的網絡系統。一般用被線連接起來的點來代表網絡。這些點被稱為節點，是網絡的參與者；線則被稱為鏈路，代表參與者之間的聯系。

如圖1所示，電網互相傳輸電力，通信網之間互相傳輸數據，交通網之間互相運輸，供水網之間互相供水，同時電網進行電力傳輸需要通信網進行控制，通信網之間互相通訊又依賴于電網的供電等。如果這些網絡中的一個節點受到攻擊而失效，這些牽制關系能使故障在網絡之間傳播。如圖2所示，一個節點受到攻擊后，最初有12個運行節點的網絡最后只剩下4個有效節點。

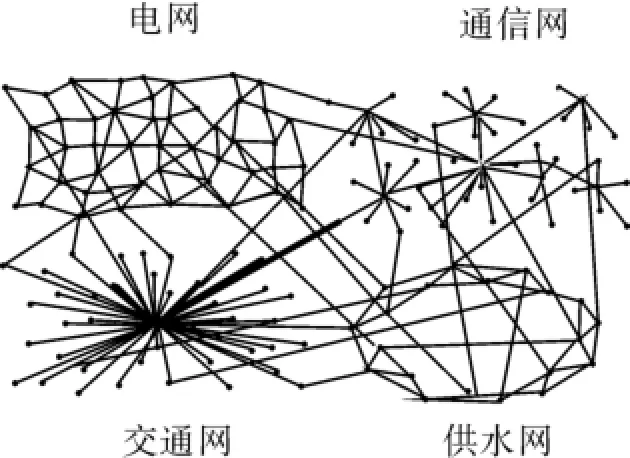
圖1 網絡示例Fig.1 A network exam ple

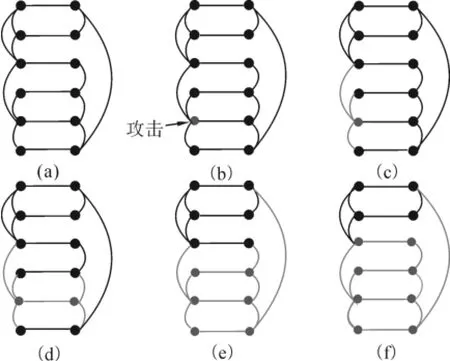
圖2 失效的傳播Fig.2 A propagation of the failure

近年來，許多實證研究證明，社會系統中的許多網絡，都滿足冪律分布［7－9］，即少數主導節點具有非常大的連接數，大多數節點的連接數甚小，以互聯網為例，如圖3所示。

圖3 全球排名前1 000網站Fig.3 The 1 000 most?visited sites on the web

圖3 勾勒了全球排名前1 000的網站，這個網絡一共有1 000個網站和2萬條有向鏈接，全球的網站分成了兩大陣營。左邊這一塊的核心是google、youtube、facebook等，右邊的核心是百度、優酷、人人網等。

如圖4所示，這1 000個網站度分布是個長尾分布，但有一個明顯的截斷。這是因為只考慮了排名靠前的網站，這個排名范圍以外的網站數據是極度不全的。從分布來看，是一個類冪律分布，斜率大概是0.8，而Barabasi等［2］估計的互聯網鏈接冪律分布指數是2.1。這有2種原因：1）近年來互聯網變得更不平等；2）只監測了重大流量的鏈接結構，相當于互聯網里的rich club，也就是說網絡中的鏈接是更不平等的。

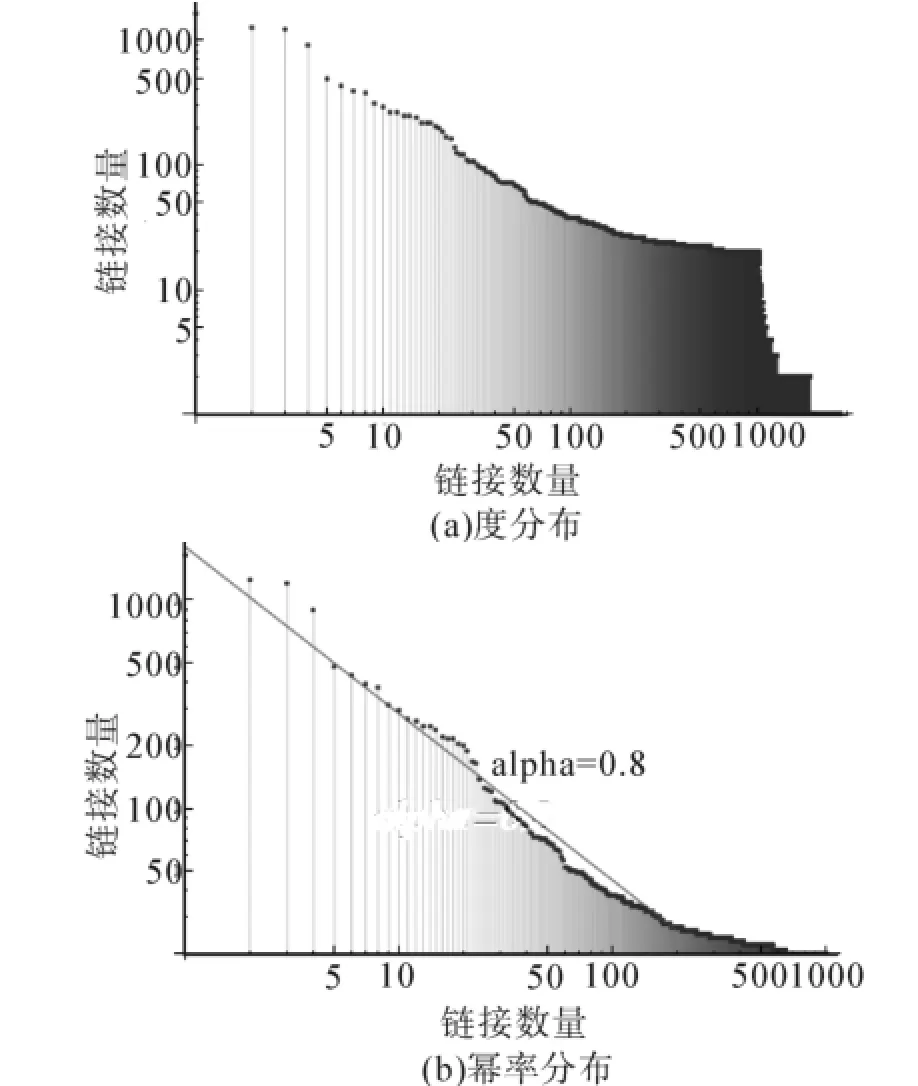
圖4 全球排名前1 000網站的度分布及冪律分布［10］Fig.4 Degree and pow er?law distribution of the 1 000 most?visited sites on the web［10］

基于這些實證，牽制控制［11］的本質通過復雜網絡中的少數節點影響網絡中的其他節點，從而實現整個網絡的同步，所需解決的問題包括：

1）可行性問題：當網絡規模很大時，控制理論中已有的判據和算法的計算復雜度往往難以承受，因此需要尋找新的有效算法；

2）經濟性問題：選取受控節點代價的最小化；

3）魯棒性問題：大規模復雜網絡往往面臨由于隨機故障或者有意攻擊而導致的節點或鏈路失效。因此，有必要研究控制系統對于隨機故障和有意攻擊的魯棒性。特別地，需要能夠給出判別大規模網絡控制系統中的關鍵節點和鏈路的有效算法；

4）演化性問題：很多實際網絡的結構和參數往往是隨時間演化的，這給系統的有效分析與控制帶來新問題，需要有適合演化網絡的判斷依據與有效算法。

面對這些問題，很重要的一點就是對網絡進行牽制［12］，使得其網絡的最終狀態滿足一定要求。但對于大規模的網絡，不可能控制其每個節點，僅能對網絡中的少數關鍵節點進行控制，通過節點間的相互耦合，從而達到控制整個網絡的目的。

1.2 復雜網絡的牽制模型［13］

給定時間t和狀態空間中的一點x（t），復雜網絡動態變化過程可表示為

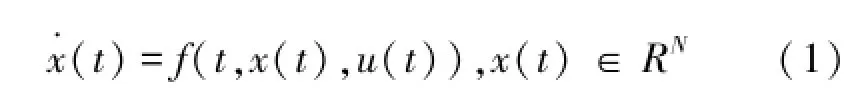
式中：輸入u（t），t時刻的狀態與輸出惟一確定。

考慮一個由N個節點構成的連續動力系統，其中第i個狀態節點的線性耦合常微分方程［14］如式（2）所示。

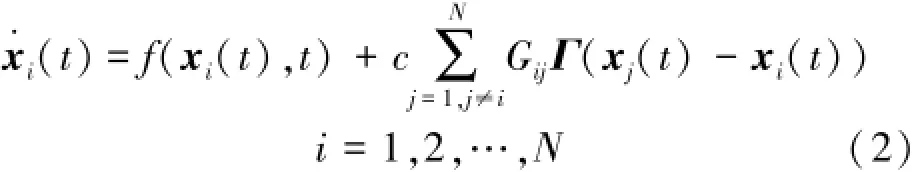
式中：N＞1為網絡節點個數；xi（t）＝[xi1（t）xi2（t）…xin（t）]T∈Rn表示i節點的狀態向量；常數c＞0表示耦合強度；Γ∈Rn×n表示外部耦合矩陣，由于f的線形性，Γ為正定；G＝（Gij）N×N表示網絡的拓撲結構，其中若存在節點j到節點i（i≠j）的連接，則Gij＞0，若存在節點i到節點j（j≠i）的連接，則Gji＞0，否則Gij＝0。G對角元素定義為式（3）。

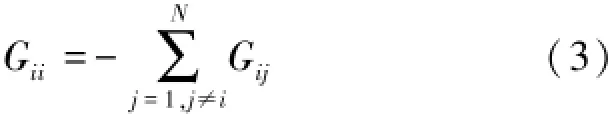
從而滿足了耗散耦合條件，如式（4）所示。

此時，式（2）可簡化為

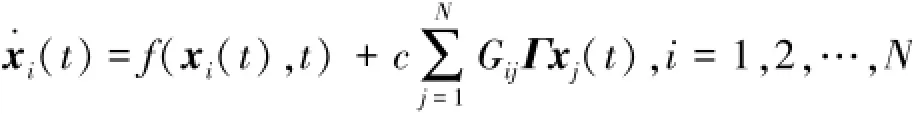
設不動點s是系統的解，如式（5）所示。

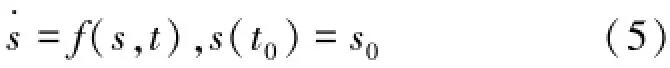
式中：s（t）可以是一個平衡點、周期軌、擬周期軌、混沌軌道，或者是多agent動態網絡的虛擬領袖。假設在網絡中僅前面l個節點（q1，q2，…，ql）為驅動節點，網絡能被描述為式（6）、（7）。

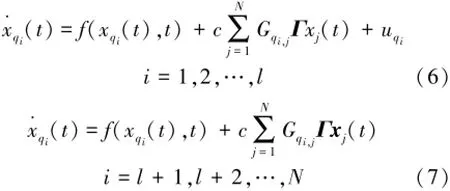
式中：l＝?δN」，0＜δ＜1，其中dqi＞0為反饋控制增益，uqi是n維線性反饋控制器。

牽制控制的目標是發現一些合適的uqi以使網絡能夠達到某個同步狀態，其中同步可表示為式（8）。

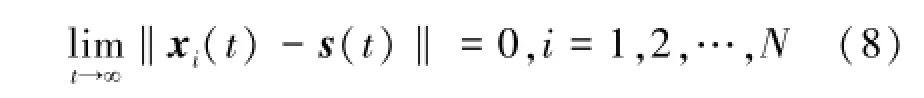
1.2.1 一般復雜網絡的同步化

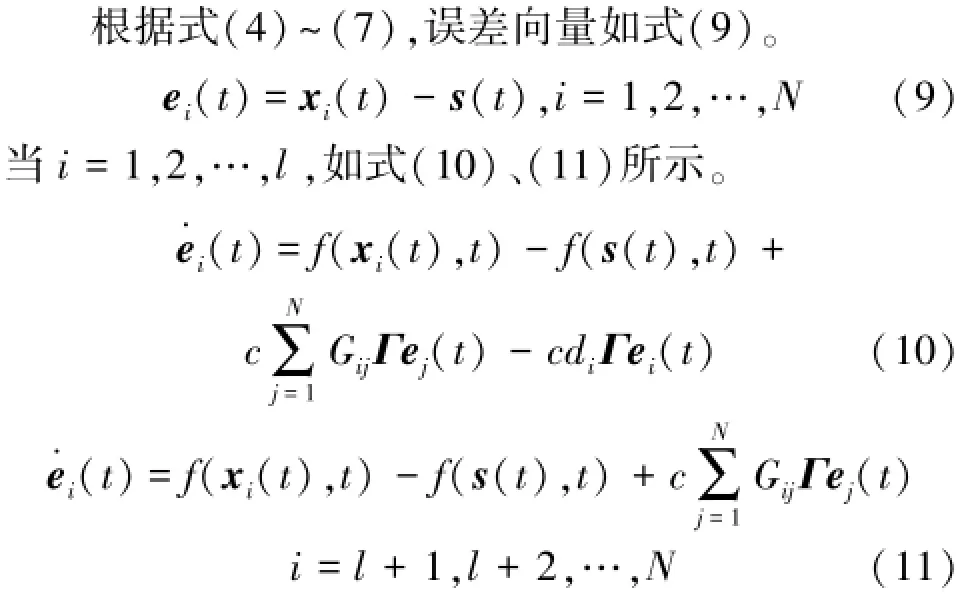
為了獲得式（10）、（11）的收斂條件，選擇Lya?punov函數為

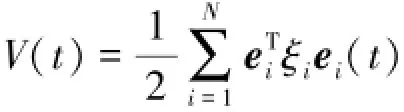
設存在K使得（x－y）T（f（x，t）－f（y，t））≤（x－y）TKΓ（x－y）?x，y∈Rn［15］成立，即滿足Lip?schitz條件。根據式（8）求導得

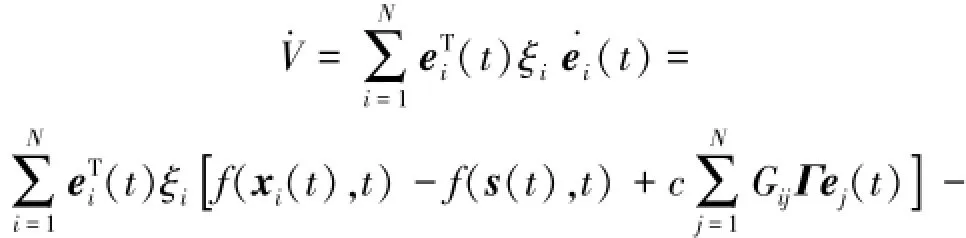
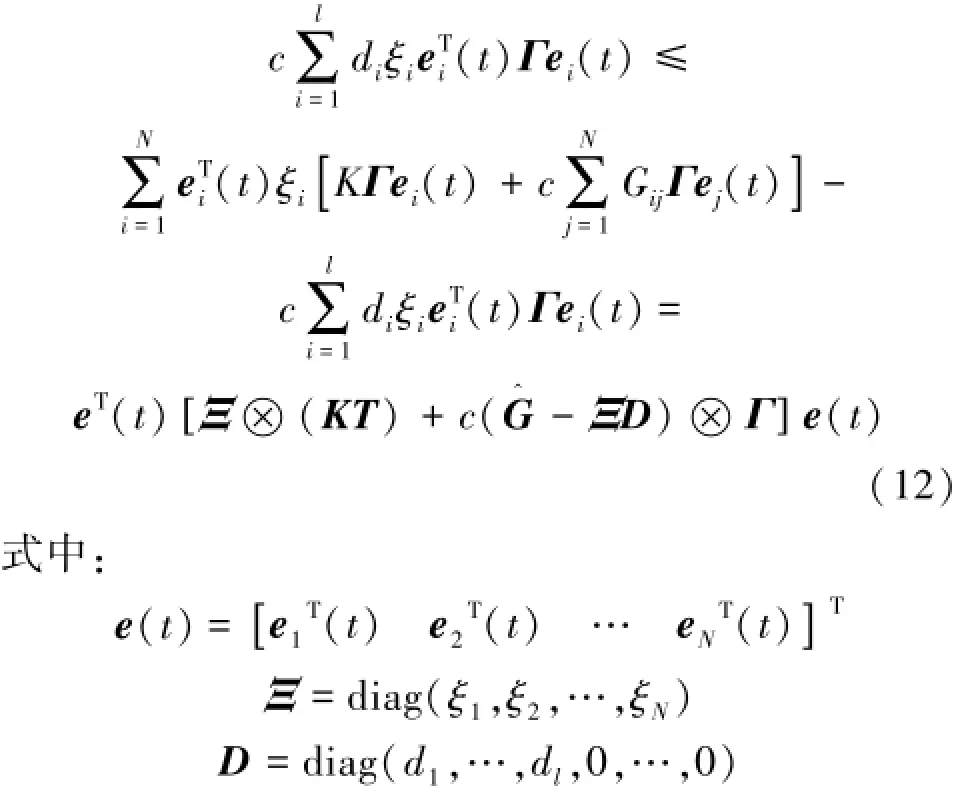
當D＝0，表明來自外部的入度很高，無需控制便能達到同步，?為kronecker積，

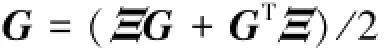
設θ＝λmax（K＋KT）／2，由于θ與K的可互換性得：

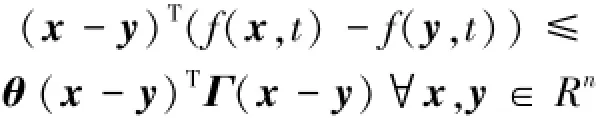
若V≤0，誤差逐漸趨向于零，則網絡同步，可得式（16）。

1.2.2 包含生成樹的復雜網絡的同步化

隨著移動技術與社會化媒體的迅速發展，人們越來越多地參與到網絡上豐富的社會活動中。人們在享受前所未有的便捷的同時，也擁有了網絡這一公共話語平臺，但同時個性會自覺的消失而群體的共性便隨之顯現出來，形成所謂的“網民群體”。網民群體常常表現為非常煩躁、多變和沖動，將選擇、判斷和處理的權利交給群體領袖。群體領袖對事件的傾向性解讀，在暗示和相互傳染的推波助瀾下，立刻會被網民接受。

給合式（6）～（8），將群體領袖作為生成樹的根節點，可得式（17）。

1.3 算法及系統運行界面

牽制控制算法具體步驟如下：

2）根據式（17）計算，如果j＝0，則網絡無需控制便可同步，轉到6），否則轉到3）；

3）如果節點來自外部的入度為零，比如Cj＝0，

－根據式（17），節點必須通過Dj進行控制，轉到4），否則轉到6）；

4）對于通過j鏈路連接的i節點，根據式（15），如果入度kirnj－1＋i≤θ／c，則節點必須被控制，轉到5），否則轉到6）

5）篩選根節點，轉到6）

6）如果j＜m，則j＝j＋1，轉到2），否則終止。

系統運行界面如圖5所示。

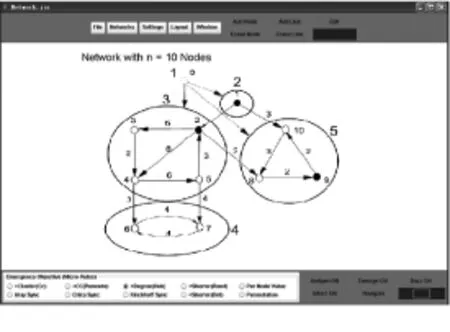
圖5 運行界面Fig.5 Running interface

2 實驗結果及分析

包含10個節點的網絡拓撲如圖5所示，可分解為5個部分，其中s為群體領袖，實心圓點為被驅動節點，用于牽制其余部分，空心圓點通過節點間的耦合連接關系被間接地控制。2，1），c＝12，N＝10，θ＝31。子網2和3子網的外部入度均為0，必須加以控制。

對于子網2，C2＝A－2＝0，根據式（17）如果d1＞≈2.583 3，子網2能同步；

對于子網3，C3＝0，＝diag（8，1，3，4）

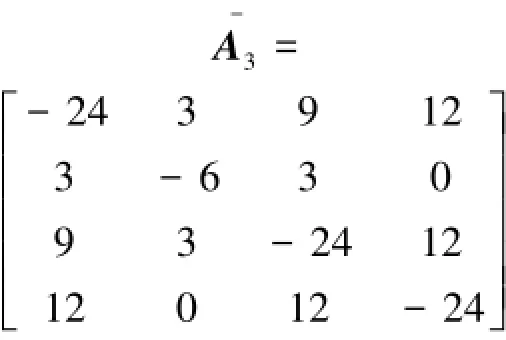
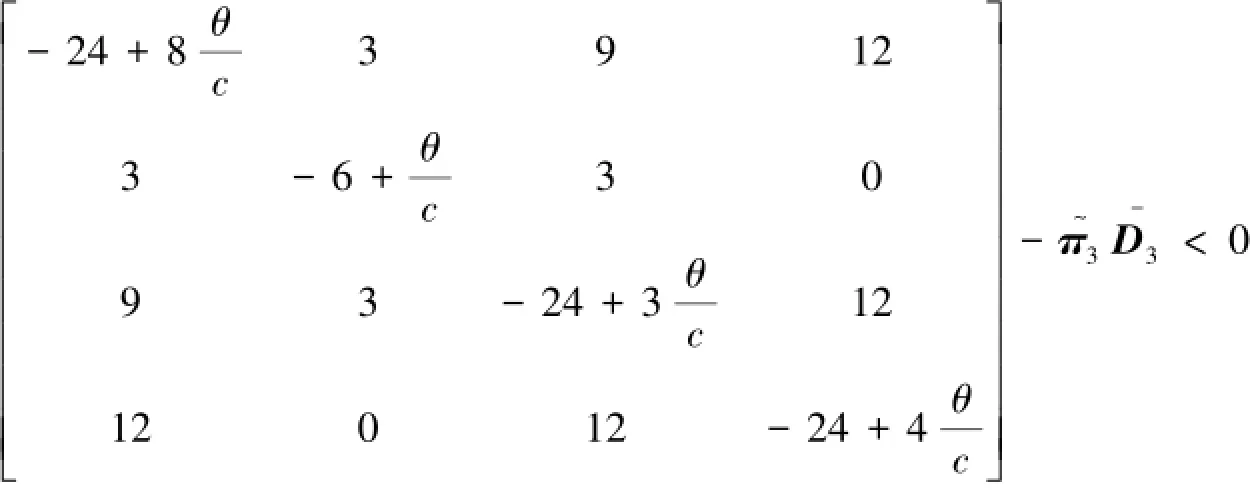
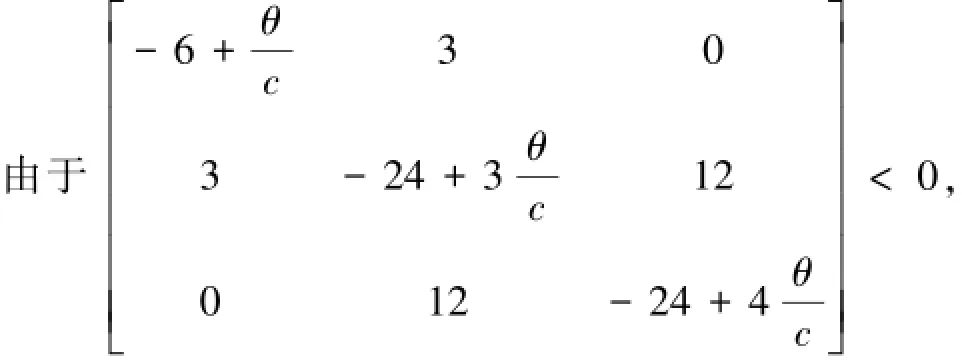
根據式（17）如果d2＜18.266 7，控制子網3中的節點2，子網3能同步；

對于子網5，C5＝diag（2，0，3），＝diag（2，3，

2.665 ，控制子網5中的節點9，子網5能同步。

綜上所述，實心節點1，2，9的d1＞2.583 3，d2＞18.266 7，d9＞2.665，圖中的網絡可同步。如圖6所示，隨著網絡規模的擴大，驅動節點的比例減小，即越是稀疏的網絡需要越多比例的驅動節點才能實現完全能控。

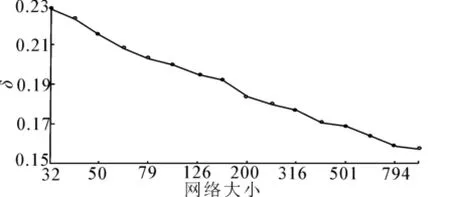
圖6 驅動節點比例與網絡規模N的關系Fig.6 Relation betweenδand N

如圖7所示，分別以ER網絡和Scale?free網絡為例，驅動節點常常都是入度低的節點，這與式（14）、（15）一致，也與現實情況一致，即入度低的網絡控制起來比較困難，入度高的網絡可通過驅動少數節點來加以控制。

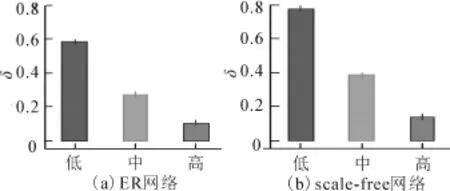
圖7 驅動節點比例與其入度的關系Fig.7 Relation betweenδand in?degree

3 結束語

本文針對一般復雜網絡和包含生成樹的復雜網絡的優化牽制控制，給出了此2種情況下復雜網絡同步的條件，最后通過系統仿真，發現越是稀疏的網絡需要越多比例的驅動節點才能實現完全能控，且入度低的節點應首先加以控制。

［1］WATTS D J，STROGATZ S H.Collective dynamics of small?world networks［J］.Nature，1998，393（6684）：440?442.

［2］BARABASIA L，ALBERT R.Emergence of scaling in ran?dom networks［J］.Science，1999，286（5439）：509?512.

［3］LIU Y Y，SLOTINE J J，BARABáSA L.Controllability of complex networks［J］.Nature，2011，473：167?173.

［4］WANGW X，NIX，LAIY C.Optim izing controllability of complex networks by minimum structural perturbations［J］.Phys Rev E，2012，85（026115）：1?5.

［5］NEPUSZ T，VICSEK T.Controlling edge dynamics in com?plex networks［J］.Nature Physics，2012（8）：568?573.

［6］YAN G，REN J，LAI Y C.Controlling complex networks：how much energy is needed？［J］.Phys Rev Lett，2012，108（218703）：1?9.

［7］NEWMAN M E J.Networks：an introduction［M］.Oxford：Oxford University Press，2010：1?20.

［8］CHEN G R，WANG X F，LI X.Introduction to complex networks：models，structures and dynam ics［M］.Beijing：High Education Press，2012：1?10.

［9］ZHOU T，WANG B H.Catastrophes in scale?free networks［J］.Chin Phys Lett，2005，22：1072?1075.

［10］Google.The 1000 most?visited sites on the web［EB／OL］.USA：Google（2011?07?19）［2012?10?25］.http：／／www.google.com／adplanner／static／top1000.

［11］RAJAPAKSE I，GROUDINE M，MESBAHIM.Dynamics and control of state?dependent networks for probing genom?ic organization［J］.PNAS，2011，108：257?262.

［12］汪小帆，李翔，陳關榮.網絡科學導論［M］.北京：高等教育出版社，2012：1?15.WANG Xiaofan，LIXiang，CHEN Guanrong.Introduction of network science［M］.Beijing：Higher Education Press，2012：1?15.

［13］CHEN G R，WANG X F，LI X.Introduction to complex networks：models，structures and dynamics［M］.Beijing：High Education Press，2012：167?256.

［14］YUW，CAO J，LIU J.Global synchronization of linearly hybrid coup led networkswith time?varying delay［J］.SIAM JAppl Dyn Syst，2008（7）：108?133.

［15］柳亭，楮衍東，張建剛，等.復雜動態網絡的牽制同步控制［J］.燕山大學學報，2010，34（5）：459?470.LIU Ting，CHU Yandong，ZHANG Jiangang，et al.Pin?ning controlled synchronization of a complex dynamical net?work［J］.Journal of Yanshan University，2010，34（5）：459?470.

仇建平，男，1973年生，講師，主要研究方向為復雜網絡、人工智能，承擔山西省回國留學人員科研資助項目、山西省自然科學基金、山西省重大科技專項基金等項目多項。發表學術論文9篇，其中5篇被EI檢索。

陳立潮，男，1961年生，教授，主要研究方向為人工智能，發表論文數十篇。

潘理虎，男，1974年生，副教授，博士，主要研究方向為煤礦安全、人工智能。

Synchronization in comp lex networks via pinning control

QIU Jianping，CHEN Lichao，PAN Lihu
（Institute of Computer Science and Technology，Taiyuan University of Science and Technology，Taiyuan 030024，China）

For the tremendous amount of nodes in complex networks，no one can control all the vertices.Only by controllingminor vertices and spinning the complex network can the synchronization of the network be achieved.The conditions for synchronization of common network and the network with spanning tree are analyzed.The algo?rithm to achieve itand the operation interface are given in this paper.The system simulation results showed that the percentage for the pinning controlled vertices becomes smaller as the network size becomes larger and the vertices with very small in?degrees should be pinned.

complex network；coupling；pinning control；spanning tree；synchronization

TP393.4

A

1673?4785（2014）06?0734?06

仇建平，陳立潮，潘理虎.牽制控制下復雜網絡的同步性研究［J］.智能系統學報，2014，9（6）：734?739.

英文引用格式：QIU Jianping，CHEN Lichao，PAN Lihu.Synchronization in complex networks via pinning control［J］.CAAI Transactions on Intelligent Systems，2014，9（6）：734?739.

10.3969／j.issn.1673?4785.201311014

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1673?4785.201311014.htm l

2013?11?07.

日期：2014?09?30.

山西省回國留學人員科研基金資助項目（2013?097）.

仇建平.E?mail：920868329＠qq.com.