一種薄壁殼體零件的靜力仿真和靜力試驗

呂忠衛, 顧 峰, 戴秀芬

（上海無線電設備研究所,上海 200090）

一種薄壁殼體零件的靜力仿真和靜力試驗

呂忠衛, 顧 峰, 戴秀芬

（上海無線電設備研究所,上海 200090）

利用有限元對薄壁殼體進行靜力學分析,并采用實物試驗對仿真結果進行驗證,建立了薄壁殼體零件設計和靜力學分析的方法。

殼體；靜力仿真；靜力試驗

0 引言

當前對機械類產品的設計要求是輕、巧、小,并在此基礎上具有相當的力學要求,能滿足產品的強度指標。這就要求在產品的開發設計時做相應仿真分析和實物靜力學試驗,以此提高設計的可靠性,節約研制成本和縮短研制周期。

1 零件設計

零件在初步設計階段就需要考慮產品的技術指標要求,從而選擇相應的材料以及采用相應的設計來滿足技術指標要求。

1.1 指標要求

對某圓柱殼體類零件,總體給出如下指標：

a）殼體重量小于350 g。

b）殼體在承受3 950 N剪力時,能同時承受1 352 Nm的彎矩,安全系數為1.5。

c）殼體長度為112 mm,直徑為127 mm。

1.2 殼體的設計

按照重量指標和力學要求,選擇鋁合金2A12-T4作為該零件的材料。表1為該材料的物理屬性。

零件設計時,充分考慮力學要求,在減重的同時,局部采用加強筋以提高殼體的力學性能。

表1 零件材料屬性

如圖1所示,殼體壁厚為2 mm,局部采用4 mm厚加強筋增加殼體強度。經分析,該零件重量為334 g,滿足指標要求。

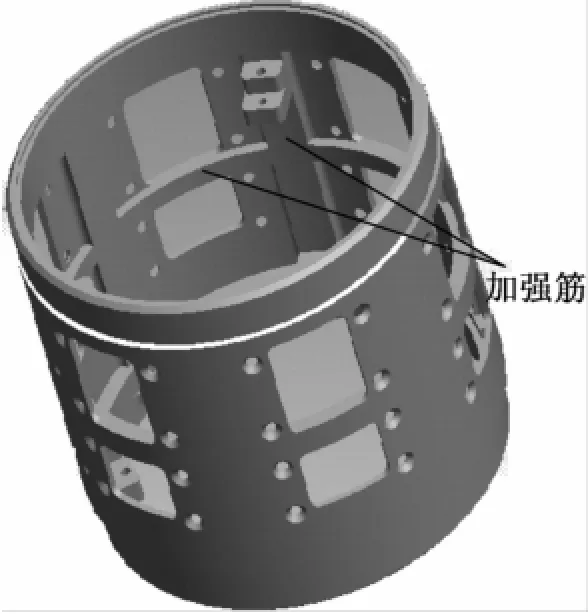
圖1 殼體三維造型

2 靜力學仿真

在完成殼體的結構設計以及材料選擇后,須對該殼體進行靜力學分析,校核其強度是否能滿足指標要求。

2.1 殼體有限元模型

殼體上的許多小孔對整個艙體的強度和剛度的影響較小,因此在有限元建模過程中把這些小孔去除不予考慮。建好的殼體有限元模型如圖2所示,模型中采用十節點四面體二階實體單元。

圖2 殼體有限元模型

2.2 施加載荷及約束條件

在有限元軟件中較難直接模擬總體所給出的條件,因此在建模過程中通過等效彎矩計算,對殼體進行適當延長便于加載。

通過等效計算,把殼體總長加長至366 mm,其中一端（用于加載載荷）延長238 mm,另一端（用于加載約束）延長16 mm,在延長后的端面上施加3 950 N的載荷就能夠模擬產生最大彎矩為1 382.5 N·m的彎矩。考慮到安全系數為1.5,須在載荷施加面施加5 925 N的剪力,同時在殼體另一端面將產生2 073.75 N·m的彎矩。

圖3為殼體的載荷與約束圖,圖中左端面加載了5 925 N的載荷,右端面進行了六自由度的約束。

圖3 殼體載荷與約束圖

2.3 計算結果

采用ANSYS軟件對圖3進行有限元分析,殼體的應力云圖如圖4所示,可以看出殼體的最大應力位于殼體右端面退刀槽處,大小為315 Mpa,低于材料的抗拉強度為425 Mpa,表明該殼體的設計能滿足力學指標要求,且剩余強度系數為1.349。

3 殼體靜力試驗

為了進一步驗證所設計薄壁殼體的力學性能,需要對實物進行靜力試驗。

3.1 試驗條件設置

圖4 殼體的應力云圖

從仿真結果可以得到,殼體在承受150%的使用載荷時,尚剩余強度系數為1.349,因此在實物靜力試驗中,設定試驗載荷為使用載荷的150%,即加載5 925 N的剪力,該剪力將在殼體另一端面產生2 073.75 N·m的彎矩。圖5為該殼體靜力試驗加載示意圖。

殼體靜力由固定板、轉接環、殼體（試驗件）、位移計、加力環和接長筒組成。固定板與轉接環的作用是固定殼體,位移計的作用是測量殼體在加載情況下的位移變化量,接長筒的作用是使過載加載在圖5所示366 mm處,加力環的作用是在試驗環Q處進行力的加載。

圖5 殼體靜力試驗加載示意圖

如圖5所示,在殼體后端固定有兩只位移計,分別是1#和2#,在殼體前端也固定有兩只位移計,分別是3#和4#。

試驗時,在Q處以試驗載荷的10%為一級,逐級加載,直至加載至100%試驗載荷（即150%使用載荷）后卸載,查驗在各級載荷作用下位移的變化量。

3.2 試驗結果

試驗結果如表2所示,1#位移、2#位移、3#位移和4#位移分別對應1#位移計、2#位移計、3#位移計和4#位移計在相應載荷時所測量的位移值。

表2 艙體靜力試驗位移測量數據

從表2數據分析,在最大過載情況下,殼體位移值僅為0.38 mm,且在卸載后,位移值迅速恢復至0.031 mm,可見,在150%使用載荷作用下,殼體并未發生塑性變形,而是仍處在彈性變形階段。

該試驗結果有利的支撐了仿真試驗的結果,從零件承受載荷和零件受力產生位移兩方面同時驗證了設計的合理性,為薄壁殼體類零件的設計提供了一條設計、仿真和實物試驗的思路。

4 結束語

本文通過有限元仿真分析和實物試驗建立了薄壁殼體類零件設計的思路,完善了薄壁殼體零件的設計與分析。

［1］程燕平.靜力學［M］.哈爾濱：哈爾濱工業大學出版社,1999.

［2］張少實.新編材料力學［M］.北京：機械工業出版社,2002.

［3］張國瑞.有限單元法［M］.北京：機械工業出版社, 1992.

［4］王勛成,邵敏.有限單元法基本原理和數值方法［M］.北京：清華大學出版社,1995.

［5］ANSYS公司北京辦事處.ANSYS入門手冊［S］. 2003.

［6］R.D.庫克,程耿東,等譯.有限元分析的概念和應用［M］.北京：科學出版社,1989.

Statics Simulation and Statics Test of a Thin-walled Shell Part

LV Zhong-wei, GU Feng, DAI Xiu-fen
（Shanghai Radio Equipment Research Institute,Shanghai 200090,China）

The statics analysis of thin-walled shell was performed via finite element.The design and statics analysis methodology of spareparts made from thin-walled shell was established according to the simulation test result.

shell；statics simulation；statics test

TJ43

A

1671-0576（2014）01-0018-03

2013-03-26

呂忠衛（1981-）,男,碩士,高級工程師,主要從事引信結構設計研究。