基于一階多重散射近似的激光引信雨滴回波模擬

王 彪, 林嘉軒, 何鴻飛

(電磁散射重點實驗室,上海 200438)

基于一階多重散射近似的激光引信雨滴回波模擬

王 彪, 林嘉軒, 何鴻飛

(電磁散射重點實驗室,上海 200438)

首先對雨粒子光學特性參數(平均反照率、消光系數、吸收系數、不對稱因子、相函數等）進行建模和計算。基于一階多重散射近似理論建立回波雷達方程,構建時域回波與入射脈沖(時間與空間分布）、粒子光學特性參數、引信參數之間的關系模型。通過改變雷達基線、孔徑面積、波束發散角、脈寬以及消光系數、不對稱因子等參數對激光引信回波進行仿真,并對其進行分析。

激光引信；相函數；消光系數

0 引言

陽光、云層、煙霧、雨雪、戰場煙塵、海面等都會對激光引信的正常工作產生影響。為了減輕和消除云霧等對激光引信的干擾,必須研究云霧的激光散射特性。

引信發射激光脈沖,雨霧以及回波脈沖的展寬、畸變、延時給探測算法帶來困難。研究環境特性的任務是尋求環境回波與目標回波的差異,包括幅度、延遲、相位、極化特性的差異。本文主要研究幅度、延遲、畸變等基本特征。由于粒子的空間和時間分布具有隨機性,掌握回波特性需要大量測試,分析不同狀態下隨機粒子的回波。不僅耗費大量的人力物力,而且環境的復雜性和狀態的隨機性使得這種做法無法實現。采用數字仿真可以通過改變輸入參數模擬不同狀態下的回波。

隨機粒子脈沖散射模型主要有蒙特卡羅多次散射模型、基于雙頻互相干函數的輻射傳輸理論模型以及一階多重散射模型和單次散射模型［1］。針對雨滴等稀疏粒子,蒙特卡羅方法難以收斂,而且激光引信的收發視場較小,普通的蒙特卡羅方法幾乎不可用。針對理想平面波和球面波,輻射傳輸理論模型有解析解,對激光引信的扁平波束無解析解。單次散射模型只把各個粒子的散射貢獻進行簡單相加,未考慮發射機到散射粒子、散射粒子到接收機之間的衰減。一階多重散射理論既考慮了散射粒子到收發機之間的衰減,又避免了光子在粒子中隨機游走過程的模擬,適用于雨滴等稀疏隨機粒子的散射回波模擬。

本文結合激光引信給出基于一階多重散射近似的回波仿真模型。該模型可以對雨滴等稀疏分布隨機粒子的回波幅度、延遲、畸變等特征進行有效模擬與分析。

1 仿真模型

光子在隨機粒子中傳播時,經歷散射和吸收過程,部分未被吸收的光子散射到探測器形成回波信號。因此,首先研究雨霧粒子的單次散射特性,然后結合激光引信參數建立脈沖散射回波模型。

1.1 隨機粒子的單次散射模型

描述單個粒子單次散射的主要參數有散射截面、吸收截面和不對稱因子。散射截面和吸收截面之和稱為消光截面,散射截面與消光截面之比為單次反照率。降雨由大小不同的粒子組成,必須考察隨機粒子的統計特性,對各項參數均作平均化處理。描述粒子隨機分布特采用吸收系數、散射系數、消光系數三個物理量,其中消光系數為吸收系數和散射系數之和。滿足一定尺度分布的粒子,其平均不對稱因子為

式中:n(r)為單位體積內粒子的粒度分布;r為粒子的半徑;Cs為半徑為r的粒子的散射截面;g為半徑為r粒子的不對稱因子。

為簡單起見,雨霧粒子通常用球形粒子等效。對球形粒子,散射截面、吸收截面、不對稱因子等可以用Mie理論精確求解［2］。對于雨粒子,光學參數可以用幾何光學近似求解,與Mie理論結果比較可知,誤差可以忽略。

隨機粒子的消光系數σe和吸收系數為σa分別為

式中:ρ為所有尺寸的粒子數濃度,即單位體積中的總粒子數;Ce為消光截面;Ca為吸收截面;〈·〉表示該量針對粒子粒度分布的加權平均。粒子平均反照率〈ω0〉=〈Cs〉/〈Ce〉。

下面以雨滴為例,給出其單次散射計算結果。雨粒子的粒度分布可以用修正伽馬分布表示為［3,4］

式中:D為粒子直徑,單位mm;c1為截取參數,單位mm―1mm―3;a為形狀因子;c2為分布的斜率因子,單位mm―1;γ通常選為1。不同降雨率時的模型參數見文獻［5］。圖1為不同降雨率時雨滴的粒度分布。

圖1 雨的粒度分布

如圖1所示,隨著降雨率增大,雨滴尺度分布范圍變大,分布的負斜率因子變小,造成雨滴分布向大直徑方向擴展。降雨率為75 mm/h時,雨滴分布向中間值集中,較小和較大的粒子數目有所減少。

表1為通過Mie理論計算獲得不同降雨率時的光學參數,這里設雨的折射率實部為1.329,虛部為2.93×10―7。

表1 不同降雨率時雨的光學參數

如表1所示,隨著降雨率增大,平均不對稱因子變大,意味著粒子總體前向散射變強,與單個粒子前向散射強的理論結果相符。由于雨滴折射率虛部在近紅外波段較小,對光子的吸收遠小于散射貢獻,造成降雨吸收系數比消光系數小兩個量級左右。隨著降雨率增大,消光系數急劇下降。由比爾定律可知,透過率增大,相應的回波越小。

1.2 隨機粒子的脈沖散射模型

光子在隨機粒子中隨機游走,在碰撞到每個粒子時,部分能量被吸收,部分能量被散射,攜帶部分能量的散射光子繼續經歷下一個粒子的碰撞,產生吸收和散射過程,直到探測器接收到未被完全吸收的散射光子,并產生響應。由于發射激光脈沖中包含大量光子,它們在隨機粒子中經歷完全不同的散射和吸收過程、游走路徑,從而造成回波脈沖與入射脈沖相比,產生一定的波形畸變、脈沖展寬、時間延遲和功率衰減。光子的游走過程可以用馬爾科夫過程描述,光子的吸收、散射直到被探測器接收的過程可以用蒙特卡羅方法有效地模擬。但對激光引信的窄視場和消光系數較小的降雨等稀疏分布介質,基于蒙特卡羅方法的數值模擬難以收斂。

一階多重散射近似模型在單次散射的基礎上,考慮了發射機到粒子、粒子到接收機之間的散射和吸收造成的衰減。在數學上,只要在雷達方程中加入衰減項即可。

假設包含粒子數ρd V的體積被激光波束照射,激光波束為單模高斯型［6］,則ρd V處激光照度即入射功率密度:

式中:P0(t)=P0(t―R1/c)為發射脈沖功率;c為光速;D為發射源到散射體的垂直距離;R1為發射機到散射體的距離;ω2(D)為散射體處激光的波束半徑;r為入射點(x,y)距波束中心點的距離。發射波束示意如圖2所示。

圖2 激光引信發射波束

圖2中d x和d y分別為距離D處激光波束在x軸和y軸方向的擴展寬度。實際仿真計算中,根據實驗測量獲得某一距離處激光波束空間強度分布,經數值擬合得到任意橫向距離上的強度,由能量守恒可得到任意距離處的波束空間強度分布［7］。激光發射脈沖呈高斯狀,實際仿真過程中,由測量數據擬合獲得激光發射脈沖波形。

設散射體到接收機的距離為R2,則接收功率密度為

式中:ρ為單位體積的粒子數;G(o)為接收視場因子;σe為消光系數;p(θi,φi;θs,φs)為入射方向(θi, φi)到散射方向(θs,φs)的散射相函數。這里使用了Henyey-Greenstein相函數,且假設散射只與入射方向和散射方向的夾角有關,則相函數為

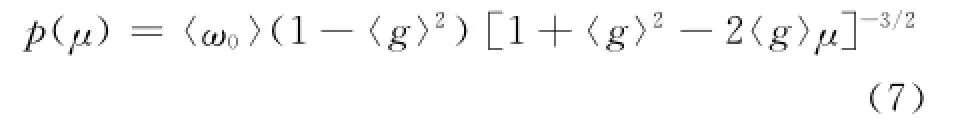
式中:μ為入射方向和散射方向夾角的余弦。

設接收截面積為Ar,則接收功率為對發射與接收交叉體積V中所有粒子散射貢獻的積分

考慮發射機到粒子、粒子到接收機之間的衰減,接收功率為

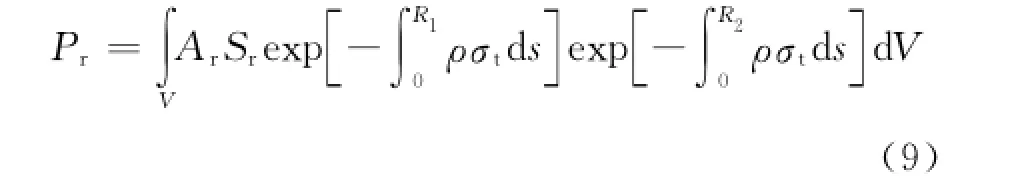
式中指數項為“發射-粒子-接收”過程中的衰減。

式(9)構建了時域回波與入射脈沖(時間與空間分布)、粒子光學特性(粒子的消光系數、反照率、不對稱因子等)、引信參數(基線、窗口面積等)之間的關系模型。

2 仿真與分析

下面通過改變基線長度、發散角和視場角中線的夾角、脈沖寬度等進行仿真,分析激光引信回波。

圖3為不同基線長度時的回波脈沖,消光系數為0.1223 m―1,脈沖寬度為3 ns,孔徑半徑為1 cm,采用交叉體制。由圖3可見,基線越長,交叉體積越大,導致回波展寬越大。由于交叉體積離彈體變遠,其功率下降,延時變大。

圖3 不同基線長度時的脈沖回波

圖4為發射波束中心線和接收視場中心線夾角變化時的回波脈沖。由圖4可見,角度越小,交叉體越大,距離越遠,導致脈寬越寬,反之亦然。

圖5是不同脈寬情況下的回波脈沖,脈寬較窄時,回波反映的是交叉體的形狀,這是激光一維距離成像的依據。脈沖較寬時,基本上保持發射脈沖的形狀。

圖4 收發視場中心線夾角變化時的回波

圖5 不同脈寬情況下的脈沖回波

另外分別改變接收口徑、消光系數,而其它參數不變時,仿真結果可知:口徑變化只改變回波功率的大小,對波形和寬度沒有影響;消光系數僅對回波功率有影響,消光系數越大,回波功率越高。但如果考慮多次散射,消光系數應該對回波脈寬有影響,這里不作進一步討論。

3 關于盲區與脈寬的討論

首先,討論盲區問題。圖6為盲區示意圖,比較圖6(a)和(b),基線AB足夠長時,光子經過多次散射進入接收視場的概率大大降低,這時近距盲區起到很好的抗干擾作用。但基線變長導致盲區過大,對目標造成漏警,如圖6(b)所示。可以增大收發視場中心線夾角φ,從而增加近距的探測范圍,如圖6(c)所示,但缺點是需要發射和接收視場尖銳,且光子經多次散射進入探測器概率增大,需綜合考慮。

圖6 盲區示意圖

其次討論脈寬問題。減小脈寬,雨滴功率將減小,可以有效抑制粒子干擾。但雨滴密度較大時,靠縮短脈沖寬度所得到的抗干擾效果不高,這時可以通過脈寬和波形來判別。目標回波寬度與波束照射目標表面有關,交叉面積小,脈寬窄,反之就寬,而雨滴的寬度與交叉體積無關。

更為重要的是,激光脈沖窄時,回波可以反應目標與雜質的分布形狀。雨滴回波反應收發視場交叉體積的形狀,相對固定。目標回波形狀與波束/目標表面相交面積有關,這取決于彈目交會的具體姿態,可以利用雨滴相對固定的波形與目標波形的不同進行判別。另外,脈寬越窄,獲取目標的特征信息越豐富,激光引信能夠充分利用這些信息區分干擾和目標。

4 結束語

本文提出基于一階多重散射近似的激光引信雨滴回波模型。與基于蒙特卡洛方法的多次散射模型相比,該模型直觀、易收斂,便于進行參數影響分析和設計驗證。模型同樣適用于薄霧、煙塵、氣溶膠等稀疏隨機粒子激光引信回波仿真。

［1］Ishimaru,A.Wave Propagation and Scattering in Random Media［M］.New York:Academic press, 1978.

［2］Bohren,C.F.,D.R.Huffman.Absorption and Scattering of Light by Small Particles［M］.New York:Wiley,1983.

［3］Deirmendjian,D.Electromagnetic Scattering on Spherical Polydispersions［M］.New York:Elsevier Press,1969.

［4］Marshall,J.S.,W.M.K.Palmer.The Distribution of Raindrops with Size［J］.Journal of Meteorology,1948,5(4):165-166.

［5］Konwar,M.,et al.Shape of the Rain Drop Size Distributions and Classification of Rain Type at Gadanki［J］.Indian Journal of Radio and Space Physics,2006,35(5).

［6］Gregory R.Osche.Optical Detection Theory for Laser Applications［J］.New York:Wiley,2002.

［7］Blanquer E.Ladar Proximity Fuze System Study［D］.Sweden:Master′s Degree Project,Stkckholm:Royal Institute of Technology(KTH), 2007.

Simulation of Laser Fuze Echo from Rain Based on First-order Multiple Scattering Approximate Method

WANG Biao, LIN Jia-xuan, HE Hong-fei
(Science and Technology on Electromagnetic Scattering Laboratory,Shanghai 200438,China)

Firstly,moeleling and computation process of optical parameter of rain particles,such as averaged albedo,extinction coefficient,absorption coefficient,asymmetry factor,phase function are given.Then the echo radar function is established based on the firstorder multiple scattering approximation,which makes connection of time domain echo to incident pulse,optical parameters of particles and fuze parameter.Simulation and analyses are implemented according to different conditions,such as radar baseline length,aperture area, pulse width,radiation angle,etc.

laser fuze;phase function;extinction coefficient

TN011

A

1671-0576(2014)04-0014-05

2014-09-25

王 彪(1986―),男,工程師,碩士,主要從事目標與環境光學特性研究。