輸入狀態穩定理論下的超混沌系統同步
顏閩秀 鄭小帆 閆明
(沈陽化工大學信息工程學院1,遼寧 沈陽 110142;遼寧大學輕型產業學院2,遼寧 沈陽 110136)
輸入狀態穩定理論下的超混沌系統同步
顏閩秀1鄭小帆1閆明2
(沈陽化工大學信息工程學院1,遼寧 沈陽 110142;遼寧大學輕型產業學院2,遼寧 沈陽 110136)
針對一類帶不確定性和擾動輸入的超混沌系統的同步問題進行了研究。基于李雅普諾夫理論和輸入狀態穩定理論,設計了一個線性狀態反饋控制器,保證兩個系統達到同步,并通過Matlab中的LMI工具箱來獲得誤差反饋增益矩陣。最后,通過對超混沌Lorenz系統和Chen系統同步的Matlab仿真,驗證了所設計的控制器的有效性,實現了兩個超混沌系統的魯棒同步。
混沌信號 超混沌系統 魯棒同步 輸入狀態穩定性(ISS) 線性矩陣不等式 李雅普諾夫理論 線性狀態反饋
0 引言
混沌信號具有非周期性、類似噪聲、天然隱蔽性、高度復雜性、長期不可預測性與易于實現等特性,非常適合應用于保密通信。1990年,Pecora和Carroll提出了混沌系統同步[1],實現了同一信號驅動下兩個耦合混沌系統的狀態同步。此后,研究者們提出了一些新的同步控制方法,如滑模控制方法[2-3]、自適應法[4-5]、主動控制法[6-7]、狀態反饋法[8-9]、脈沖同步法[10-11]、觀測器法[12-13]等。
1989年,Eduardo D.Sontag針對非線性系統提出了輸入-狀態穩定(input-to-state stability,ISS)的概念[14],用來消除外部擾動輸入帶來的影響。隨后輸入狀態穩定的研究得到了廣泛的重視[15-17]。然而,這一理論應用到混沌系統同步的成果很少見。
本文針對一類帶不確定性和外界擾動的超混沌系統的同步問題進行了輸入狀態穩定控制研究,設計了線性誤差反饋控制器來保證誤差系統漸近穩定。最后,通過仿真驗證了本文設計的控制器的有效性。
1 同步誤差系統的描述
假設驅動系統和響應系統分別為:
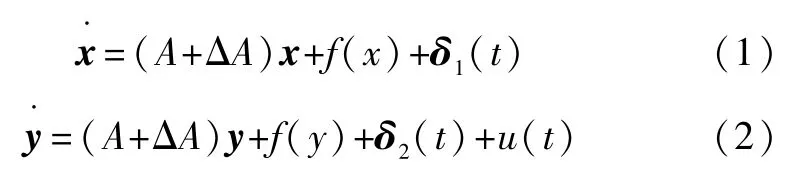
式中:x和y∈Rn為系統的n維狀態向量;A∈Rn×n為系統的線性部分;f(x),f(y)∈Rn為系統的非線性部分; ΔA∈Rn×n描述的是系統的不確定性;δ1(t)和δ2(t)∈Rn為系統的外部干擾向量;u(t)為控制輸入。
同步誤差系統可以寫成:
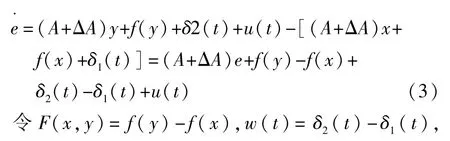
則有:
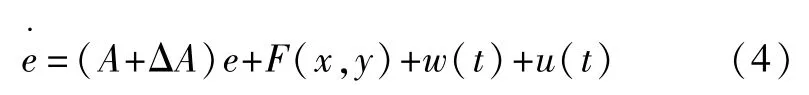
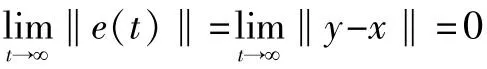
2 線性狀態控制器的設計與分析
定理1 對于誤差系統(3),如果存在正實數ε、正定的對稱矩陣X和任意的矩陣Y,滿足下面的線性矩陣不等式(linear matrix inequality,LMI):

系統存在輸入狀態反饋控制器保證其漸近穩定,并且增益矩陣K=YX-1,證明如下。
選取Lyapunov函數為V=eT(t)Pe(t),其中P>0且PT=P。將函數對時間求導,得到:
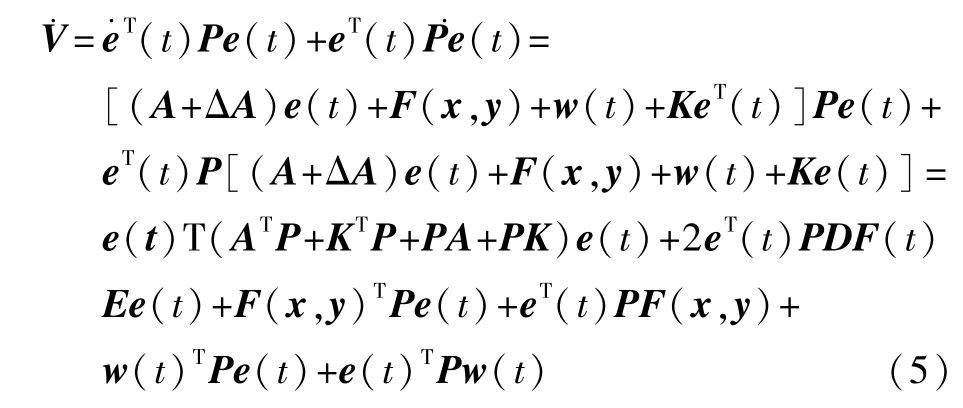
而2xTDF(t)Ey≤εxTDDTx+ε-1yTETEy,則有:
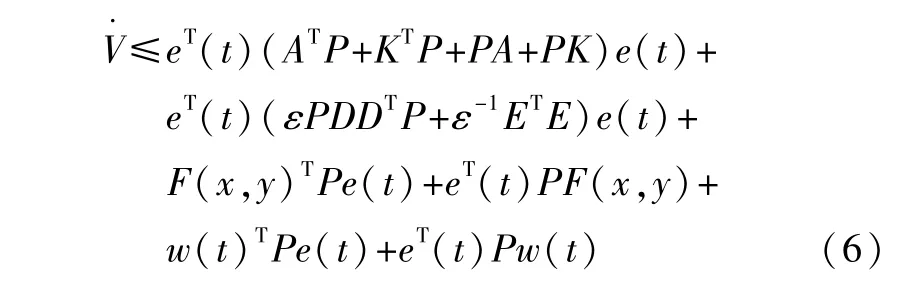
將上述不等式左乘ε,令P=εP,則有:

根據定理,得到下面的不等式:
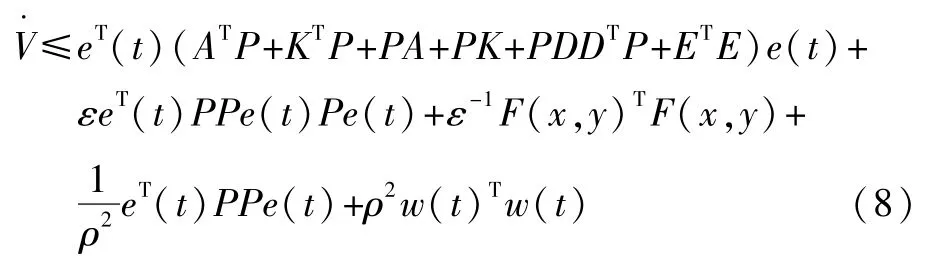
而‖f(y)-f(x)‖≤L‖y-x‖,則可得到:
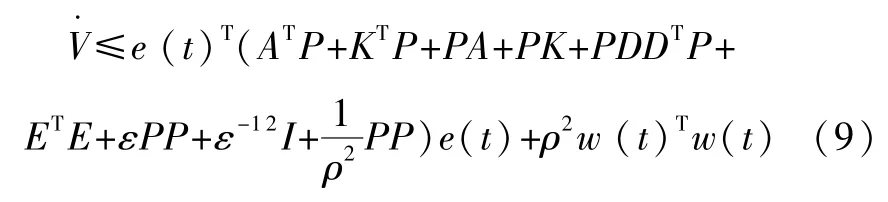
如果式(10)成立,即:
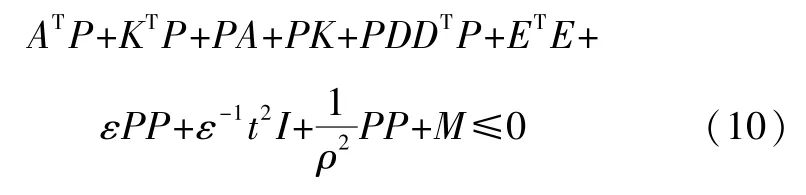
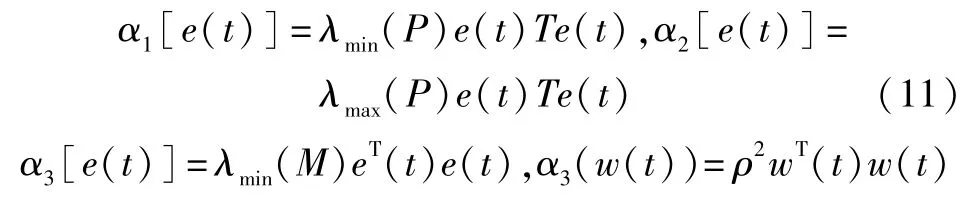
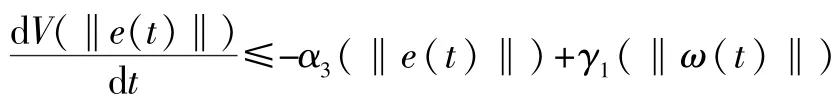
應用Schur補定理,得到下面的線性矩陣不等式:
如果存在整實數ε,正定的對稱矩陣X和任意的矩陣Y滿足線性矩陣不等式,那么就可實現輸入狀態穩定控制,并且增益矩陣K=YX-1。
3 仿真分析與討論
為了驗證所設計的同步控制器的有效性,本文選取超混沌Lorenz和Chen系統為例進行研究。超混沌Lorenz系統可以用式(13)來表示,即:
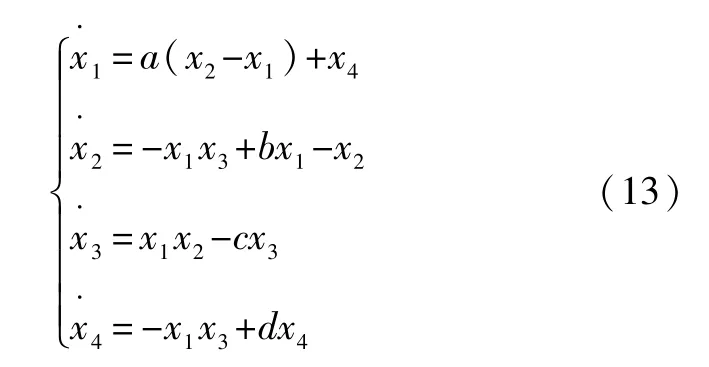
式中:a=10;b=28;c=8/3;d=1.3。
超混沌Chen系統可以用式(14)來表示:
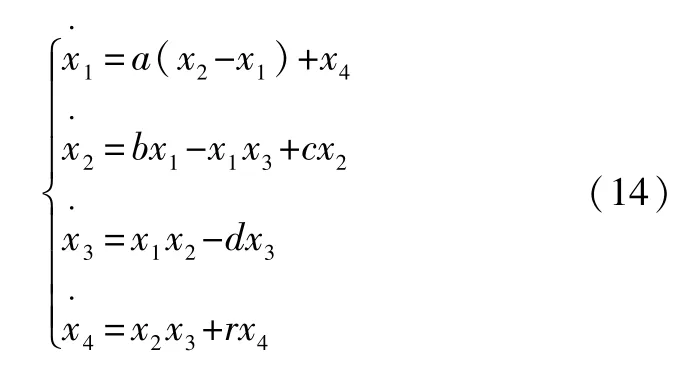
式中:a=35;b=7;c=12;d=3;r=0.5。
3.1 超混沌Lorenz系統的同步
假設
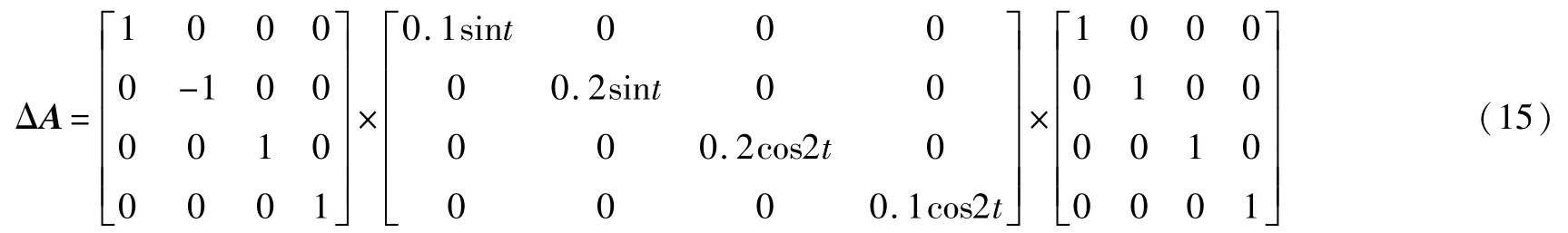
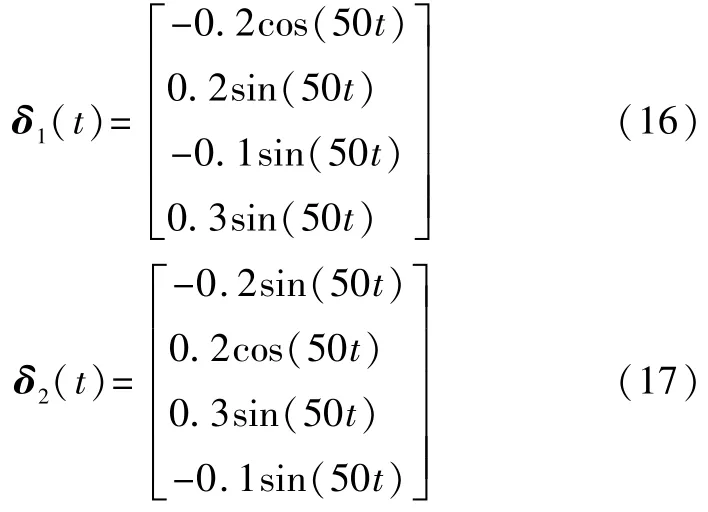
選取驅動系統和響應系統的初始值分別為: [x1(0),x2(0),x3(0),x4(0)]=(1,2,-1,2),[y1(0), y2(0),y3(0),y4(0)]=(-2,2,1,0)。令M=I,ρ=0.1,l= 87。用Matlab中LMI工具箱解線性矩陣不等式,得到增益矩陣:

通過仿真,兩個超混沌Lorenz系統的同步誤差曲線如圖1所示。從圖1可以看出,響應系統在10 s施加控制器后漸近跟蹤上驅動系統,同步誤差也漸近趨向于零。
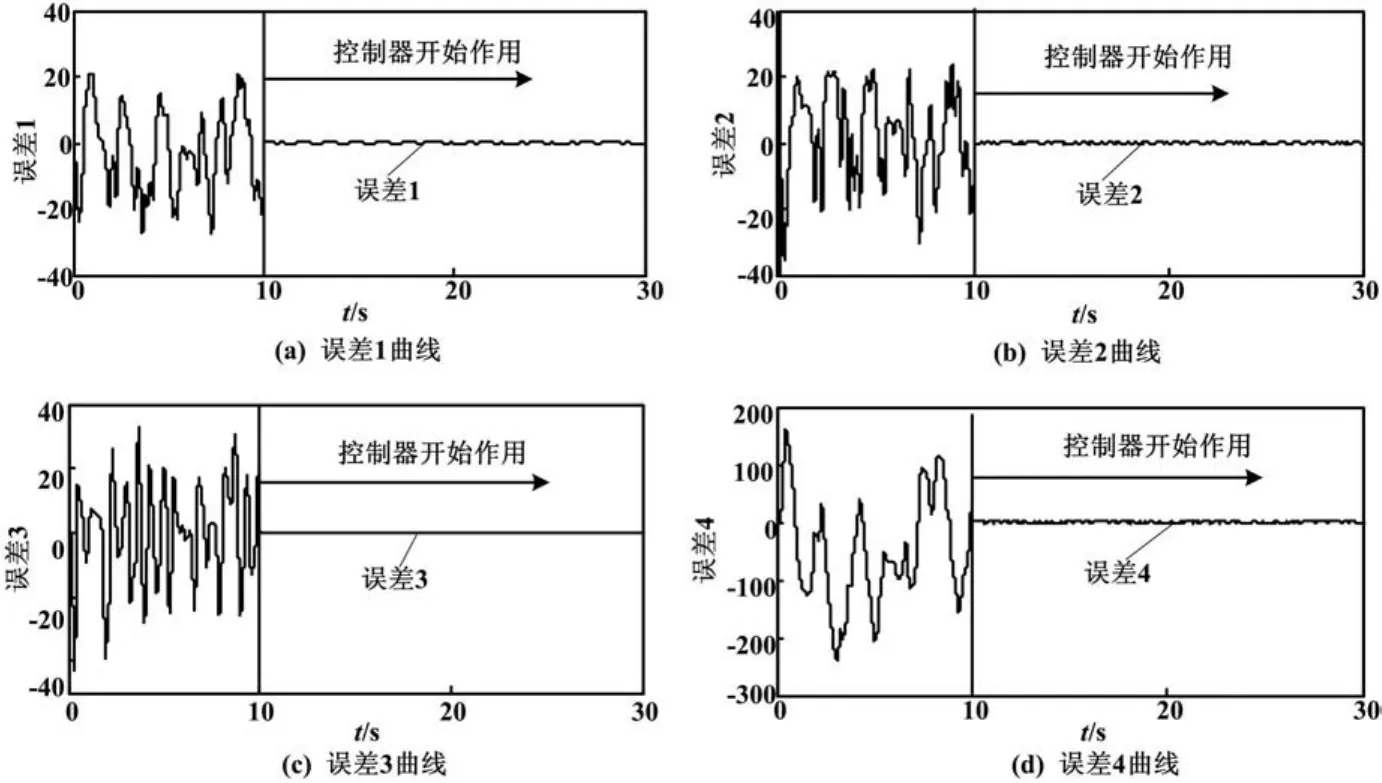
圖1 Lorenz系統的同步誤差曲線Fig.1 Synchronization error curves of the Lorenz system
3.2 超混沌Chen系統的同步
假設
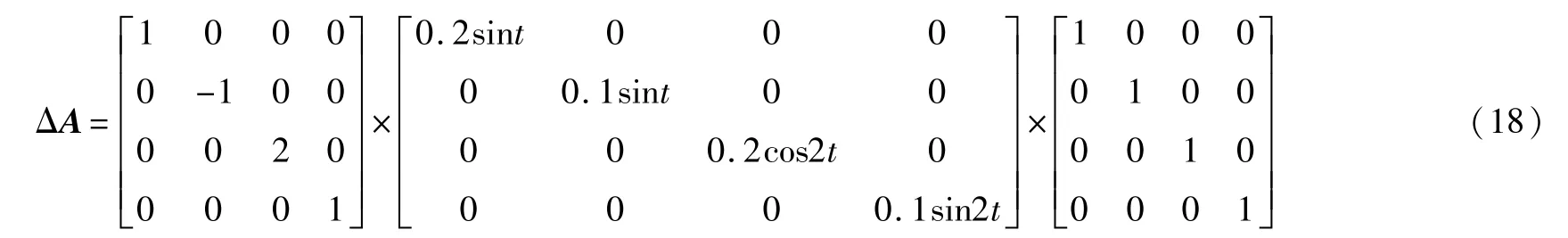
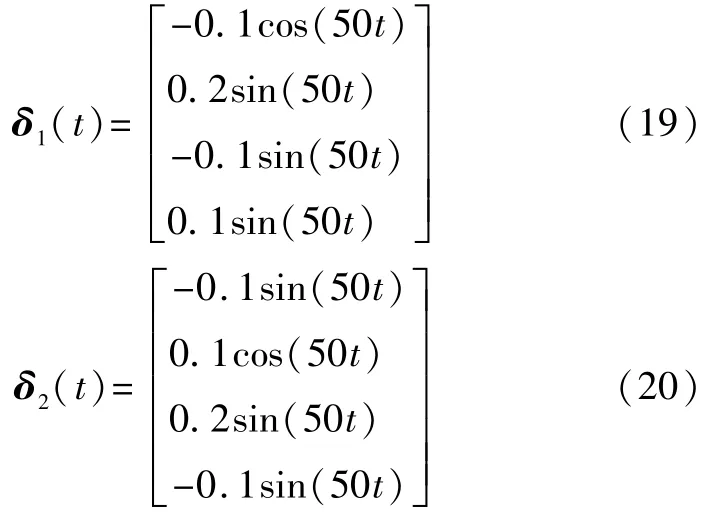
選取驅動系統和響應系統的初始值分別為:[x1(0), x2(0),x3(0),x4(0)]=(2,5,-1,2),[y1(0),y2(0),y3(0), y4(0)]=(-3,1,2,3)。令M=I,ρ=0.1,l=77.5。用Matlab中LMI工具箱得到增益矩陣:

兩個超混沌Chen系統的同步誤差曲線如圖2所示。在外部干擾存在的情況下,未施加控制器時驅動系統不能跟蹤響應系統,10 s后施加所設計的控制器,誤差狀態曲線漸近收斂到零。
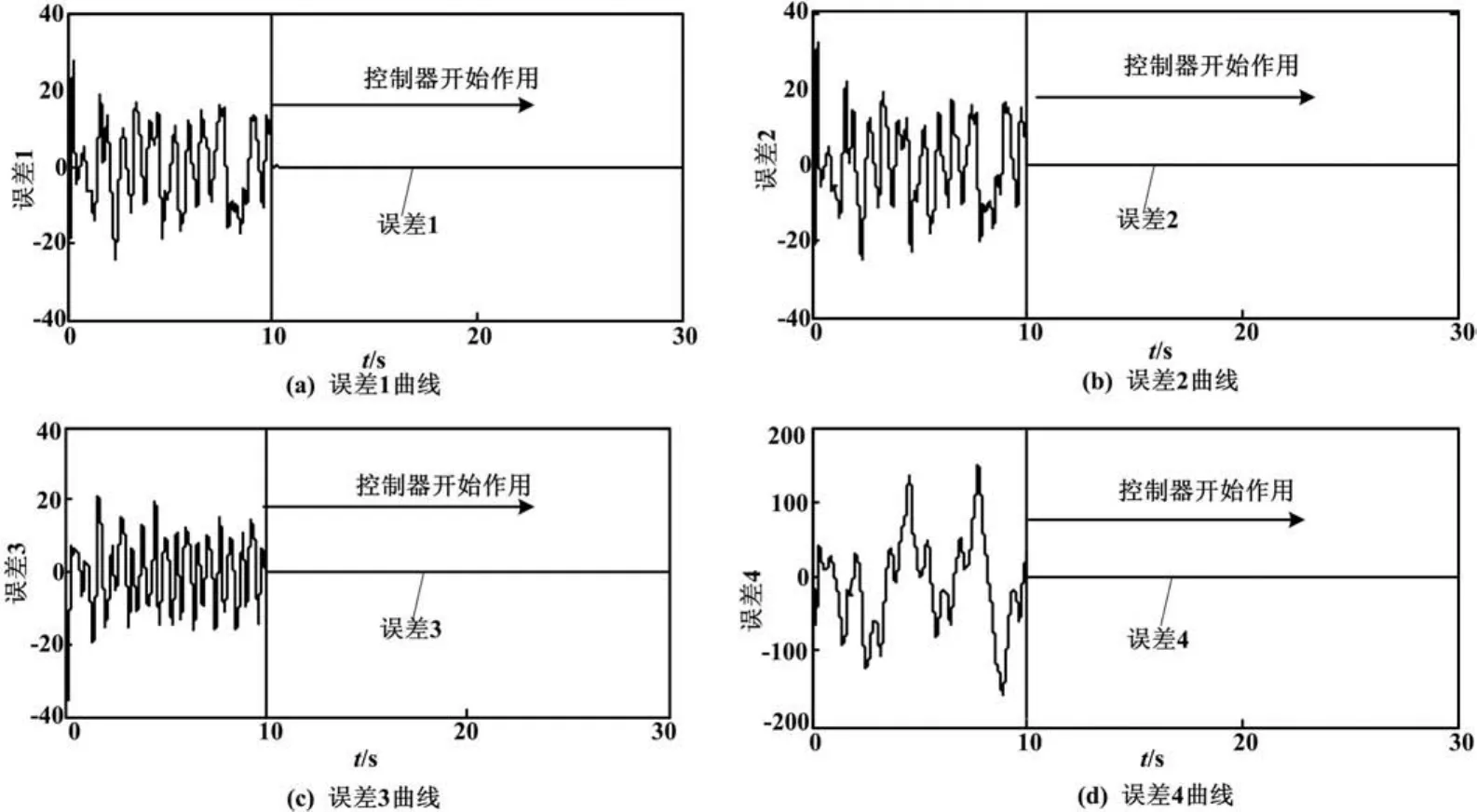
圖2 驅動和響應系統的同步誤差曲線Fig.2 Synchronization error curves of the slave system and the master system
4 結束語
本文主要研究了一類帶不確定性和外部擾動輸入的超混沌系統的同步問題。利用輸入狀態穩定理論和Lyapunov穩定理論,給出了線性誤差反饋控制器的設計方法及求解反饋增益矩陣的線性矩陣不等式,并將這種混沌系統同步方法應用于超混沌Lorenz和Chen系統。數值仿真驗證了所設計控制器的有效性。該控制器實現了兩個超混沌系統的魯棒同步。
[1] Pecora L M,Carroll T L.Synchronization in chaotic systems[J]. Physical Review Letters,1990,64(8):821-824.
[2] 高遠,羅文產,戴喜生,等.不確定性超混沌系統的積分滑模同步控制研究[J].自動化儀表,2012,33(5):15-17.
[3] 李潔,吳忠強.混沌系統的快速收斂有限時間滑模自適應控制[J].自動化儀表,2009,30(11):34-37.
[4] Zhang Jian,Xu Hongbing,Wang Houjun.Adaptive synchronization of Chua's system with uncertain inputs[J].Chinese Physics,2006, 15(5):953-957.
[5] Li X F,Leung A C S,Han X P,et al.Complete(anti-)synchronization of chaotic systems with fully uncertain parameters by adaptive control[J]. Nonlinear Dynamics,2011,63(1-2):263-275.
[6] 顏閩秀,樊立萍.混沌系統的主動自適應滑模修正投影同步[J].自動化儀表,2013,34(2):23-25.
[7] Yassen M T.Chaos synchronization between two different chaotic systems using active control[J].Chaos,Solitons&Fractals,2005, 23(1):131-140.
[8] Chen H H,Sheu G J,Lin Y L,et al.Chaos synchronization between two different chaotic systems via nonlinear feedback control[J].Nonlinear Analysis:Theory,Methods&Applications,2009,70(12):4393-4401.
[9] Ahn C K.T-S fuzzy H∞synchronization for chaotic systems via delayed output feedback control[J].Nonlinear Dynamics,2010, 59(4):535-543.
[10] Jiao H,Qiao Y,Miao J,et al.Exponential synchronization of coupled neural networks with impulsive control[J].Scientific Journal of Control Engineering,2013,3(4)254-260.
[11] Yang X S,Cao J D,Lu J Q.Stochastic synchronization of complex networks withnonidentical nodes via hybrid adaptive and impulsive control[J].CircuitsandSystemsI:RegularPapers,IEEE Transactions on Circuits and Systems,2012,59(2):371-384.
[12] 姚利娜,高金峰,廖旎煥.實現混沌系統同步的非線性狀態觀測器方法[J].物理學報,2006,55(1):35-41.
[13] 劉虎,張樹京,董德存,等.高維混沌同步控制及其在保密通信中的應用[J].自動化儀表,2001,22(10):17-18.
[14] Sontag E D.Smooth stabilization impliescoprime factorization[J]. Automatic Control,IEEE Transactions on Automatic Control,1989, 34(4):435-443.
[15] Liu J,Liu X,Xie W C.Input-to-state stability of impulsive and switching hybrid systems with time-delay[J].Automatica,2011, 47(5):899-908.
[16] Huang S,James M R,Ne?ic D,et al.Analysis of input-to-state stability for discrete time nonlinear systems via dynamic programming[J]. Automatica,2005,41(12):2055-2065.
[17] Jiang Z P,Wang Y.Input-to-state stability for discrete-time nonlinear systems[J].Automatica,2001,37(6):857-869.
Robust Synchronization of Hyperchaotic Systems under Input-to-state Stability Theory
The synchronization of hyperchaotic systems with uncertainty and disturbance input is investigated.Based on Lyapunov theory and input-to-state stability theory,the linear state feedback controller is designed,to guarantee synchronization of two systems and the error feedback gain matrix is obtained through the LMI toolbox in Matlab.The effectiveness of the controller designed is verified through the Matlab simulation of synchronization for hyperchoatic Lorenz system and Chen system,robust synchronization of two hyperchaotic systems can be implemented.
Chaotic signal Hyperchaotic system Robust synchronization Input-to-state stability(ISS) Linear matrix inequality(LMI) Lyapunov theory Linear state feedback
TP29
A
國家科技支撐計劃基金資助項目(編號:2012BAF09B01);
遼寧省自然科學基金資助項目(編號:201202092)。
修改稿收到日期:2014-02-18。
顏閩秀(1972-),女,2009年畢業于東北大學控制理論與控制工程專業,獲博士學位,副教授;主要從事變結構控制、智能控制的研究。

