基于Curvelet變換的隧道裂隙水GPR數據處理研究

朱自強，朱 賀*，魯光銀，王凡，譚 潔

（1．中南大學地球科學與信息物理學院，長沙 410083；2．中國水電顧問集團貴陽勘測設計研究院，貴陽 550081）

基于Curvelet變換的隧道裂隙水GPR數據處理研究

朱自強1，朱 賀1*，魯光銀1，王凡2，譚 潔1

（1．中南大學地球科學與信息物理學院，長沙 410083；2．中國水電顧問集團貴陽勘測設計研究院，貴陽 550081）

應用地質雷達探測隧道內部裂隙水的分布狀況時，受隧道鋼筋網的影響以及噪聲干擾，導致探測信號中弱有效信號難以識別。Curvelet變換可以對二維信號從頻率、角度和空間位置實現有效反射波和干擾波的分離及降噪處理，應用Curvelet變換對含鋼筋網干擾的裂隙水模型的探地雷達模擬數據進行波場分離和降噪處理，在壓制直達波、去除鋼筋層反射信號及多次反射的基礎上，可以有效地提取出含裂隙水所引起的反射波信號。將該方法應用到汝郴高速某隧道實測探地雷達數據中，較好地去除了鋼筋層反射信號的影響，準確地判斷出了裂隙水的空間分布位置，證明了所提出方法的有效性。

Curvelet變換；探地雷達；隧道裂隙水；波場分離；降噪

0 引言

探地雷達法［1－2］是近些年來迅速發展起來的一種高分辨率、高效率的勘探方法，目前在隧道勘測中，特別是探測巖溶裂隙水方面應用較多［3－6］。由于隧道周圍裂隙水被密集的鋼筋層覆蓋，用探地雷達對隧道裂隙水探測時會受到鋼筋層反射的干擾，因此，需要對雷達數據進行處理，去除干擾和噪聲，從而提取有效的異常信號。劉斌等［7］將復信號技術應用到探地雷達對地下裂隙水的探測中，對雷達數據中的異常分別從振幅、頻率和相位等各方面進行綜合分析，提高了預報精度和準確性，但沒能從根本上克服探地雷達法抗干擾能力弱的缺點。劉四新等［8］用鉆孔探地雷達對巖溶裂隙進行勘探，勘探效果較好，但具有探測上方位不確定性和成本較高的缺點。鄒海林等［9］基于小波變換對探地雷達信號進行處理，李才明［10］基于小波能譜分析對巖溶區探地雷達進行目標識別。小波變換很好地解決了時頻同步問題，而且對一維分段平穩信號的表達具有最佳性能，但是對于描述二維圖像信息卻存在諸多缺點［11－13］。

Candes等人［14－15］在1999年提出了第一代Curvelet變換，并于2002年提出了實現更簡單、運行速度更快、更便于直觀理解的第二代Curvelet變換算法。在此之后，他們又于2005年提出了兩種基于第二代Curvelet 變換理論的快速離散實現方法［16］，即USFFT（unequally-spaced fast Fourier transforms）和Wrapping兩種快速離散算法。2008年以來，該方法在地球物理資料處理尤其是地震信號處理中得到了迅速地研究和應用［17－20］。在國內，仝中飛等人［21］提出了迭代閾值法壓制地震信號中的隨機噪聲，取得了很好的效果。潘雪輝［22］提出了一種用Curvelet變換壓制地震資料中線性噪聲的方法，為地震信號中線性噪聲的壓制問題提供了較好地解決方法。

Curvelet變換建立在小波變換的基礎上，增加了一個方位參數，解決了小波變化在處理二維信號時的不足，而探地雷達檢測數據主要為描述一定深度范圍內剖面的二維信號，這讓作者萌生思路，利用Curvelet變換對探地雷達數據進行處理研究。在對Curvelet變換方法研究基礎上，將其應用到隧道裂隙水的探地雷達檢測資料處理中。本研究首先模擬了在含有覆蓋鋼筋層和裂隙水的混凝土中的探地雷達波場，并通過Curvelet變換對模擬波場進行去除直達波、提取水層信息、降噪等一系列數據處理流程，提取出有效的裂隙水異常信息；隨后將該方法應用到汝郴高速某隧道實測地質雷達數據，獲取了隧道內裂隙水異常的空間分布，通過鉆孔注漿驗證，證明了此方法的有效性。

1 Curvelet變換基本原理

小波變換在信號處理中的應用得到了很大的發展，遺憾的是，由一維小波所生成的可分離小波只具有有限的方向，因此在處理圖像邊緣時的效果不是很好。Curvelet變換除了與小波變換一樣具有尺度和位移參數，還增加了一個方位參數，因此具有更好的方位識別能力，可以精確表達出圖像中邊緣的方向信息。

1．1 連續Curvelet變換

Curvelet變換是利用基函數與信號（或函數）的內積形式來實現信號（或函數）的稀疏表示，表示為：

其中：φj，k，l表示Curvelet函數；j、k、l分別表示尺度、位置和方向參數。

Curvelet變換在頻域內采用窗函數U來實現的。分別定義徑向窗函數W（r）、r∈（1／2，2）和角度窗函數V（t），t∈［－1，1］，二者滿足式（2）與式（3）。

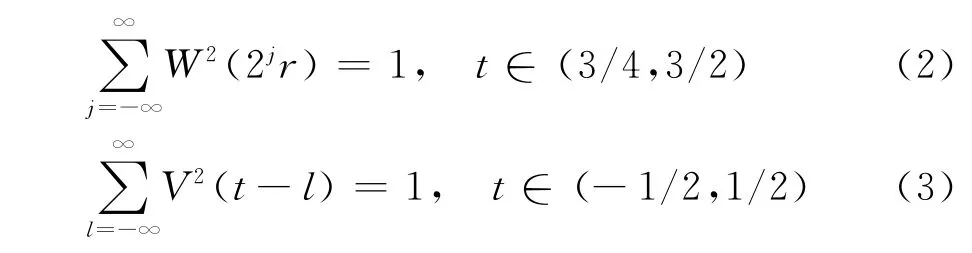
對于每一個j≥j0，在頻域中定義窗函數Uj如式（4）。

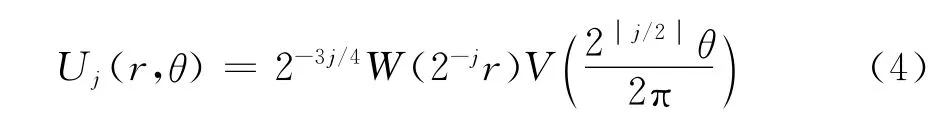
綜上所述，我們可以得到Curvelet變換公式：

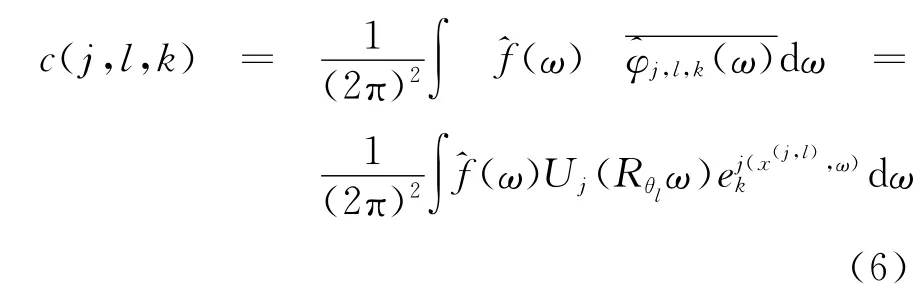
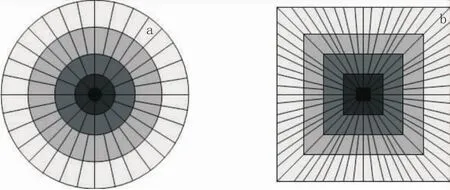
圖1 Curvelet變換示意圖Fig．1 Curvelet transform schematic diagram

1．2 離散Curvelet變換

在直角坐標系下f［t1，t2］，0≤t1，t2＜n為輸入，Curvelet變換離散形式為：

1．3 離散Curvelet變換快速實現方法

本研究采用基于USFFT算法的快速離散Cur-velet變換方法，實現過程如下：

1）對于給定的直角坐標系下二維函數f［t1，t2］，0≤t1，t2＜ω進行2DFFT，得到其二維頻率域表達式：

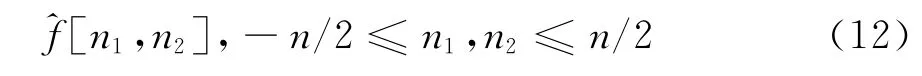
2）在頻率域，對每一對（i，j），對函數＾f［n1，n2］重新采樣，得到函數采樣值：

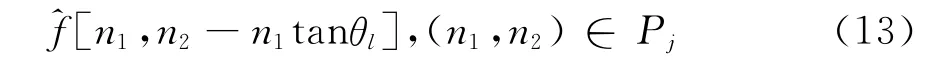
其中：Pj＝｛（n1，n2）：n1，0≤n1≤n1，0＋L1，j，n2，0≤n2≤n2，0＋L2，j｝；L1，j表示窗函數支撐區間的長度；L2，j表示支撐區間的寬度。

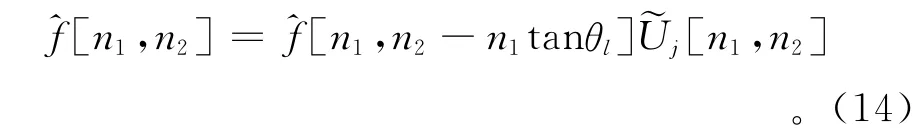
1．4 Curvelet變換的非線性逼近能力

Curvelet變換之所以比小波變換更適合表示二維信號，其主要原因在于Curvelet變換比小波在二維平面具有更好的稀疏性。假設f∈L2［0，1］為一條曲線的光滑部分，分別用小波變換和Curvelet變換對其分解，再分別選擇最佳的M個系數對函數進行重構，得到三種變換下的的最佳逼近它們的逼近誤差分別為：

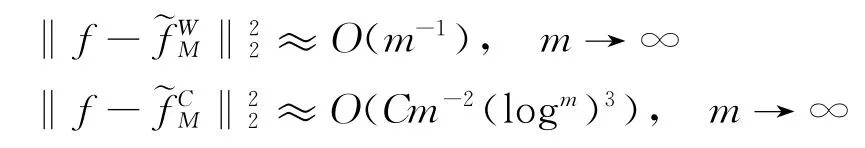
從重構誤差式中可以看出，Curvelet變換的逼近率要優于小波變換。Curvelet變換之所在表示二維曲線時有更好的逼近率，主要在于它在小波變換的基礎上增加了方位參數，使得它具有多方向性、多尺度性、波動性和各向異性的特點，這也使得用更少的Curvelet系數就能表示二維信號的主要特征。

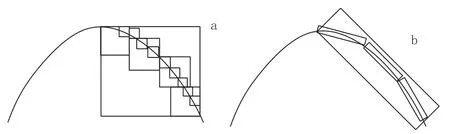
圖2 小波和Curvelet對二維曲線逼近示意圖Fig．2 Schematic of two－dimensional curve approximation with wavelet and Curvelet

2 模擬數據處理分析

針對表層存在鋼筋干擾下的含裂隙水混凝土模型進行數值模擬，模型大小為5．2 m×1．28 m，混凝土介電常數ε0為9，電導率σ0為0．01 s／m。距離表層0．3 m處設置一排鋼筋，半徑0．01 m。鋼筋層下方設置一個水平和一個傾斜含裂隙水，橫截面大小均為0．8 m×0．08 m，介電常數ε1為81，電導率σ1為0．05 s／m，模擬天線頻率為400 MHz。模型剖面和雷達模擬剖面如圖3所示。

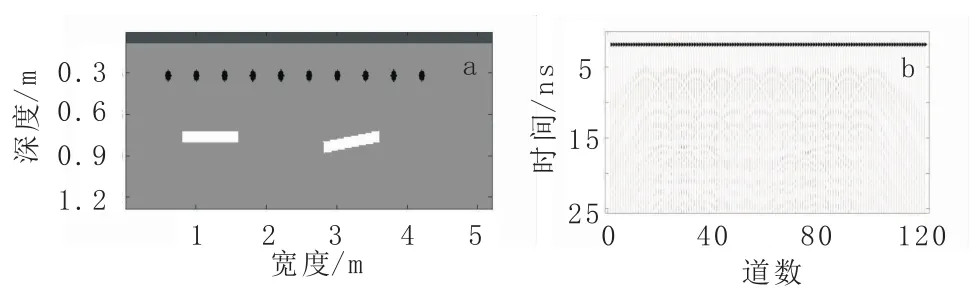
圖3 雷達數值模擬Fig．3 GPR numerical simulation

在圖3中，表層直達波強度較高，弱化了下面鋼筋層和裂隙水層的反射信號。將總波場變換到Curvelet域后，然后在角度窗函數下選擇變換域中θ＝0（θ為方向因子）附近的Curvelet系數進行重構，得到直達波的波場信號，進而分離得到的直達波波場信號和剩余波場信號（圖4）。

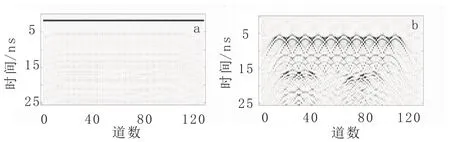
圖4 波場分離Fig．4 Wave field separation

當直達波去除后，下面鋼筋層和裂隙水層的反射信息加強，但是二次反射和干擾信息的存在干擾了異常信號，通過Curvelet變換的降噪功能可以去掉二次反射及其他干擾信號。基于Curvelet變換的特點，前人提出了各種關于降噪的閾值方法［23－24］，本研究采取一種自適應閾值方法［25］，即隨著尺度的改變，每一層閾值可以相應地改變。閾值函數表達式如下：其中 sigma為噪聲的方差估計值；N為Curvelet域系數矩陣大小；s為Curvelet域尺度分解下的層數。

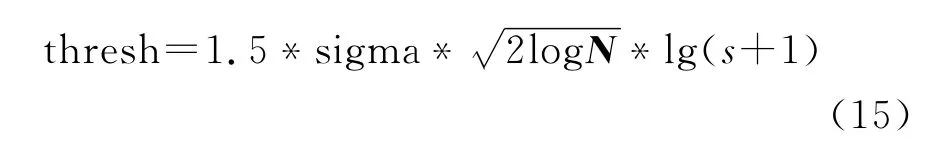
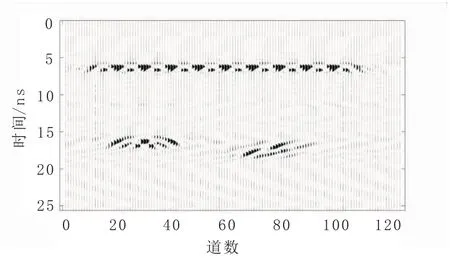
圖5 波場降噪Fig．5 Wavefield denoising

圖5為sigma系數設為700時降噪的效果圖，降噪后，鋼筋和裂隙水的異常信息已非常明顯。原始二維信號在經過Curvelet變換后會得到的一系列Curvelet系數矩陣，將這些系數矩陣在MATLAB中生成時間－頻率圖像，通過對比原始圖像異常位置可以識別出包含有效信號和干擾信號的矩陣。如果我們只需要裂隙水的異常信息，只需對這些離散化的系數矩陣進行人工識別，并挑選出含裂隙水信息的系數矩陣，進行Curvelet反變換，得到只含裂隙水異常信息的二維數據。圖6為應用Curvelet變換波場分離方法得到的裂隙水異常信息數據。

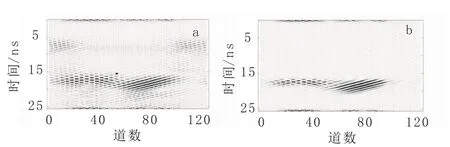
圖6 提取裂隙水波場信息Fig．6 Wave signal extraction of fissure water

處理結果顯示，用Curvelet變換對雷達模擬數據的處理效果良好，波場分離和降噪都能夠基本達到目的。兩個方向有差異的裂隙水的異常信息在處理過程中表現出不同的處理效果，這也說明了Curvelet變換在處理圖像信息時帶有很強的方向選擇性。由于水平的裂隙水在方向上與上面鋼筋層保持平行，用Curvelet變換離散化圖像信息時，水平裂隙水與鋼筋層的信息在角度窗函數選擇下沒能夠完全分離，只能夠通過尺度來分離部分信息。這樣傾斜的裂隙水異常信息才會顯得比水平裂隙更明顯。

3 實測數據處理分析

在Curvelet變換方法研究和模擬處理的基礎上，對汝郴高速公路某隧道內采集所得探地雷達數據進行處理。探測目的是找出隧道邊墻和底部存在的裂隙水，確定這些裂隙水的位置及相關信息，為工程治理工作提供較好的參考信息。探測中使用的天線為400 MHz，采樣點數設為512，參考設計方案，鋼筋間距約為50 cm。

圖7（a）為截取采集數據中某一異常位置信息，直達波和鋼筋產生的干擾信息強度較強，同時數據中含有一些噪聲干擾。首先我們要將有效異常信息和鋼筋層干擾信息及直達波信息分離開，提取含有有效異常信息的數據。圖7（b）為分離出的鋼筋層信息及一些干擾信息，圖7（c）為提取得到的含有裂隙水層異常信息的波場。由于波場分離更多在于角度窗下的選擇，圖7（b）中鋼筋層干擾和直達波與圖7（c）中有效信息被基本分離開，但仍然有一些因為與裂隙水異常信息方向一致而未被分離的遺留信息，且存在一些噪聲。遺留下的干擾信息強度較弱，可以通過Curvelet降噪功能，應用自適應尺度閾值法，通過尺度窗的選擇進行降噪，取sigma系數為48 000得到降噪后的異常圖7（d）。圖7（d）異常信息清晰，進而可以判斷裂隙水的空間位置。

根據探測和處理結果，對發現的異常位置進行鉆孔驗證如圖8所示。驗證結果支持了該方法對于裂隙水空間位置的判斷，并在該異常位置進行了注漿治理，總注漿量為10 T左右水泥和38 T左右化學漿。對于本次探測中發現的其他幾個異常位置，用文中所述方法進行分析并打鉆注漿，在判斷得到的異常較大位置都能注入不同量的漿液，驗證了該處理方法的準確性與可行性。

4 結論

1）基于Curvelet變換，從波場分離的角度來提高探地雷達異常信號的辨識度，較好地解決了直達波和鋼筋層強反射對下層異常信息的干擾問題。

2）角度參數的增加使得Curvelet變換在二維信號的分離上有了很強的優勢，但是在干擾信息與有效信息方向性一致的情況下，分離效果并不理想。

圖7 工程應用實例Fig．7 Examples of application engineering

圖8 現場鉆孔照片Fig．8 Photos of drilling

3）閾值函數的選取直接關系到Curvelet降噪的效果，采取適應不同尺度的自適應閾值函數，基本能夠達到消除噪聲的目的，但閾值函數thresh沒有從角度去適應系數矩陣，找到同時適應尺度和角度的閾值函數將是下一步急需解決的問題。

［1］ 李大心．探地雷達方法與應用［M］．北京：地質出版社，1994．

［2］ 楊天春，呂紹林，王齊仁．探地雷達檢測道路厚度結構的應用現狀及進展［J］．物探與化探，2003，27（1）：79－82．

［3］ 楊龍江，閻滿存．探地雷達在隱伏巖溶區工程地質勘探中的應用［J］．物探化探計算技術，1999，21（2）：172－176．

［4］ 葛雙成，邵長云．巖溶勘察中的探地雷達技術及應用［J］．地球物理學進展，2005，20（2）：476－481．

［5］ 李孟娟，李川．探地雷達檢測隧道襯砌厚度的研究［J］．物探化探計算技術，2008，30（3）：231－234．

［6］ 李仁海，楊磊，許新剛，等．地質雷達探測技術在巖溶地形勘察中的應用［J］．物探化探計算技術，2009，31（5）：442－446．

［7］ 劉斌，李術才，李樹忱，等．復信號分析技術在地質雷達預報巖溶裂隙水中的應用研究［J］．巖土力學，2009，30（7）：2191－2196．

［8］ 劉四新，曾昭發，徐波．利用鉆孔雷達探測地下含水裂縫［J］．地球物理學進展，2006，21（2）：620－624．

［9］ 鄒海林，寧書年，林捷．小波理論在探地雷達信號處理中的應用［J］．地球物理學進展，2004，19（2）：268－275．

［10］ 李才明，王良書，徐鳴潔，等．基于小波能譜分析的巖溶區探地雷達目標識別［J］．地球物理學報，2006，49（5）：1499－1504．

［11］WALKER J S，CHEN Y．Image denoising using treebased wavelet subband correlations and shrinkage［J］．Optical Engineering，2000，39（11）：2900－2908．

［12］楊鳳娟，羅省賢．小波變換在探地雷達檢測鋼筋中的應用［J］．物探化探計算技術，2009，31（4）：354－360．

［13］黃敏，朱德兵，郭政學，等．連續小波變換在探地雷達信號分析中的應用研究［J］．物探化探計算技術，2012，34（5）：593－598．

［14］CANDES E J，DONOHO D L．Curvelets：A surprisingly effective nonadaptive representation for objects with edges［R］．DTIC Document，2000．

［15］STARCK J，CANDèS E J，DONOHO D L．The curvelet transform for image denoising［J］．Image Processing，IEEE Transactions on．2002，11（6）：670－684．

［16］CANDES E，DEMANET L，DONOHO D，et al．Fast discrete curvelet transforms［J］．Multiscale Modeling＆Simulation，2006，5（3）：861－899．

［17］Neelamani R，Baumstein A I，Gillard D G，et al．Coherent and random noise attenuation using the curvelet transform［J］．The Leading Edge．2008，27（2）：240－248．

［18］姜宇東，楊勤勇，何柯，等．基于曲波變換的地面微地震資料去噪方法研究［J］．石油物探，2012，51（6）：620－624．

［19］吳愛弟，趙秀玲．基于曲波變換的地震信號去噪方法［J］．中國石油大學學報：自然科學版，2010，34（003）：30－33．

［20］張云強，張培林，王國德，等．基于曲波變換和色度模型的彩色圖像去噪［J］．中國圖象圖形學報，2012，17（012）：1472－1477．

［21］仝中飛，王德利，劉冰．基于Curvelet變換閾值法的地震數據去噪方法［J］．吉林大學學報：地球科學版，2008：48－52．

［22］潘雪輝．曲波變換在地震信號去噪中的應用［D］．西安：西安理工大學，2009．

［23］HERRMANN F J，HENNENFENT G．Non-parametric seismic data recovery with curvelet frames［J］．Geophysical Journal International，2008，173（1）：233－248．

［24］HERRMANN F J，MOGHADDAM P，STOLK C C．Sparsity-and continuity-promoting seismic image recovery with curvelet frames［J］．Applied and Computational Harmonic Analysis，2008，24（2）：150－173．

［25］劉靜．地震圖像噪聲壓制在Curvelet域的閾值選取與噪聲定位［D］．成都：西南交通大學，2011．

Processing of GPR data in tunnel fissure water based on Curvelet transform

ZHU Zi-qiang1，ZHU He1*，LU Guang-yin1，WANG Fan2，TAN Jie1
（1．School of Geosciences and Info-Physics，Central South University，Changsha 410083，China；2．HYDROChina Guiyang Engineering Corporation，Guiyang 550081，China）

When we detect the distribution of fissure water in tunnel with ground penetrating radar，it is hard to identify the weak effective signal because of the influence of mesh reinforcement and noise．Curvelet transform can achieve effective wave field separation and denoising of two－dimensional signal from the frequency，angle and spatial location．The Curvelet transform is applied to wave field separation and signal denoise processing by using of GPR simulated data from fissured water which is disturbed seriously by the existence of mesh reinforcement．After the direct signal suppression，removal of the reflected signal and multiple reflections from mesh reinforcement，we can effectively extract the reflected wave signal which is caused by the water bearing structure crack．Our method is applied to real data measured in a tunnel of the Ruchen highway．The results show that after removal of the reflected signal from mesh reinforcement we can accurately determine the location of fissure water，which proves the effectiveness of the proposed method．

Curvelet transform；ground-penetrating radar（GPR）；fissure water in tunnel；wavefield separation；denoising

P 631．4

A

10．3969／j．issn．1001-1749．2014．05．10

1001-1749（2014）05-0571-06

2014-03-33 改回日期：2014-06-22

國家自然科學基金項目（41174061）；中南大學自由探索計劃（2011QNZT011）

朱自強（1964-），男，教授，博士生導師，主要從事地質災害探測與監測工作，E-mail：13507319431＠139．com。

*通訊作者：朱賀（1988-），男，碩士，主要從事地球物理信號處理研究，E-mail：zhuhe24＠sina．com。